The Lotka-Volterra equations, which describe a predator-prey system, must be one of the more famous dynamic systems. There are many generalizations and applications outside of biology.
Wikipedia has a nice article, which I used as the basis for this simple model.
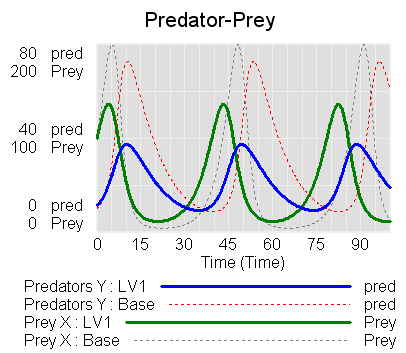
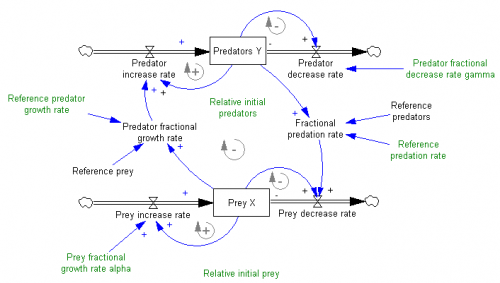
You can find an equilibrium at (Relative initial predators = 3, Relative initial prey = 0.5). An interesting experiment is to determine whether that point is stable.
Lotka-Volterra.vpm (runs in any Vensim version)
Lotka-Volterra-Alt.vpm (an alternative version that enlarges the diagram slightly and moves most of the graphs to a control panel on a second view)
Another version of the model, which requires an advanced version of Vensim or the Model Reader, uses a subscript (array) to randomize the initial conditions for the predator and prey levels. That allows you to see the effect of the parameters over a variety of random realizations in the predator-prey phase space.
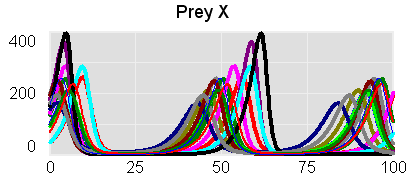Lotka-Volterra+Array.vpm (requires Vensim DSS or Pro, or the free Model Reader)
Update: I wrote a bit more on this topic here.
Can you please mail the Vensim equations of predator-prey system above.
Thanks
See my other comment – if you’re still having trouble I can post the vmf or mdl version.
The various solutions of prey-predator model will show oscillatory nature of the population of the two species in a state of “dynamic equilibrium” even though there are very very few preys.
If stochastic nature (e.g., random noise) is incorporated into the prey-predator model, prey (or predatory) might be extingushied and thus no dynamic equilibrium solution.
Leif Gustafsson, “Poisson simulation-a method for generating stochastic variations in continuous system simulation,” Simulation, 74: 5, 264-274, 2000.