There’s an interesting discussion of forest tipping points in a new paper in Science:
Global Resilience of Tropical Forest and Savanna to Critical Transitions
Marina Hirota, Milena Holmgren, Egbert H. Van Nes, Marten Scheffer
It has been suggested that tropical forest and savanna could represent alternative stable states, implying critical transitions at tipping points in response to altered climate or other drivers. So far, evidence for this idea has remained elusive, and integrated climate models assume smooth vegetation responses. We analyzed data on the distribution of tree cover in Africa, Australia, and South America to reveal strong evidence for the existence of three distinct attractors: forest, savanna, and a treeless state. Empirical reconstruction of the basins of attraction indicates that the resilience of the states varies in a universal way with precipitation. These results allow the identification of regions where forest or savanna may most easily tip into an alternative state, and they pave the way to a new generation of coupled climate models.
Science 14 October 2011
The paper is worth a read. It doesn’t present an explicit simulation model, but it does describe the concept nicely. The basic observation is that there’s clustering in the distribution of forest cover vs. precipitation:
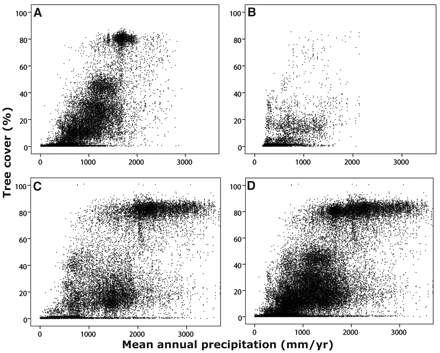
Hirota et al., Science 14 October 2011
In the normal regression mindset, you’d observe that some places with 2m rainfall are savannas, and others are forests, and go looking for other explanatory variables (soil, latitude, …) that explain the difference. You might learn something, or you might get into trouble if forest cover is not-only nonlinear in various inputs, but state-dependent. The authors pursue the latter thought: that there may be multiple stable states for forest cover at a given level of precipitation.
They use the precipitation-forest cover distribution and the observation that, in a first-order system subject to noise, the distribution of observed forest cover reveals something about the potential function for forest cover. Using kernel smoothing, they reconstruct the forest potential functions for various levels of precipitation:
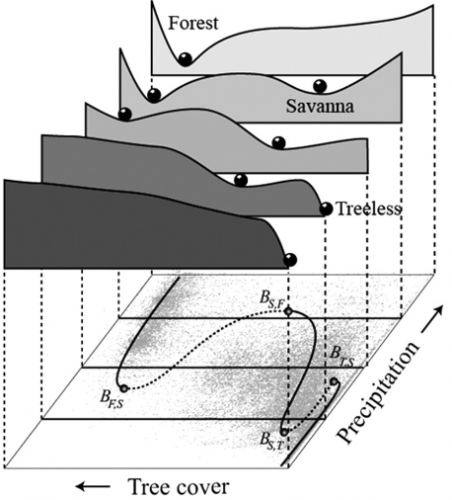
Hirota et al., Science 14 October 2011
I thought that looked fun to play with, so I built a little model that qualitatively captures the dynamics:
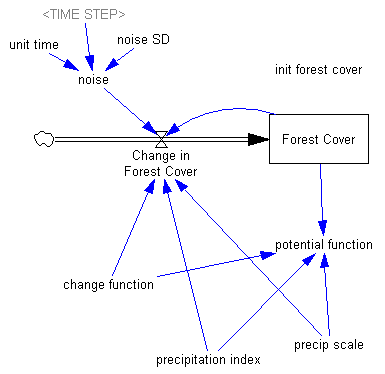 The tricky part was reconstructing the potential function without the data. It turned out to be easier to write the rate equation for forest cover change at medium precipitation (“change function” in the model), and then tilt it with an added term when precipitation is high or low. Then the potential function is reconstructed from its relationship to the derivative, dz/dt = f(z) = -dV/dz, where z is forest cover and V is the potential.
The tricky part was reconstructing the potential function without the data. It turned out to be easier to write the rate equation for forest cover change at medium precipitation (“change function” in the model), and then tilt it with an added term when precipitation is high or low. Then the potential function is reconstructed from its relationship to the derivative, dz/dt = f(z) = -dV/dz, where z is forest cover and V is the potential.
That yields the following potentials and vector fields (rates of change) at low, medium and high precipitation:
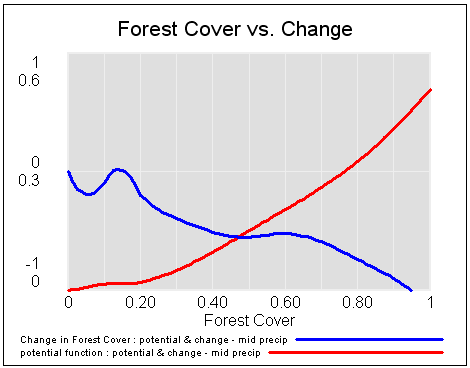
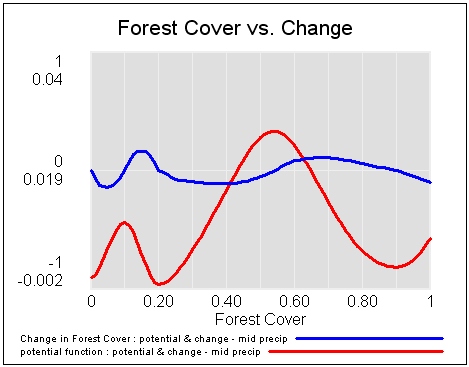
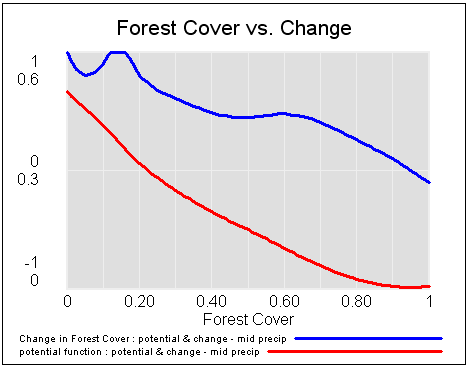
If you start this system at different levels of forest cover, for medium precipitation, you can see the three stable attractors at zero trees, savanna (20% tree cover) and forest (90% tree cover).
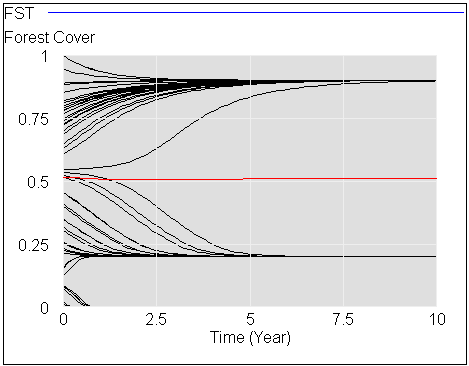
If you start with a stable forest, and a bit of noise, then gradually reduce precipitation, you can see that the forest response is not smooth.
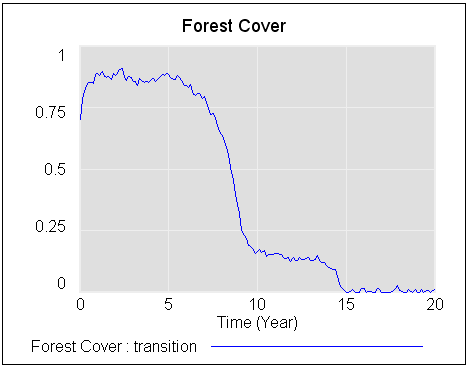
The forest is stable until about year 8, then transitions abruptly to savanna. Finally, around year 14, the savanna disappears and is replaced by a treeless state. The forest doesn’t transition to savanna until the precipitation index reaches about .3, even though savanna becomes the more stable of the two states much sooner, at precipitation of about .55. And, while the savanna state doesn’t become entirely unstable at low precipitation, noise carries the system over the threshold to the lower-potential treeless state.
The net result is that thinking about such a system from a static, linear perspective will get you into trouble. And, if you live around such a system, subject to a changing climate, transitions could be abrupt and surprising (fire might be one tipping mechanism).
The model is in my library.

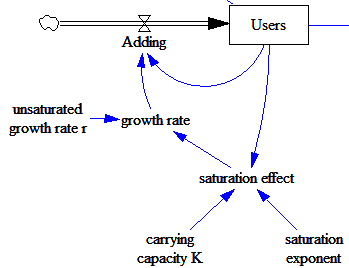
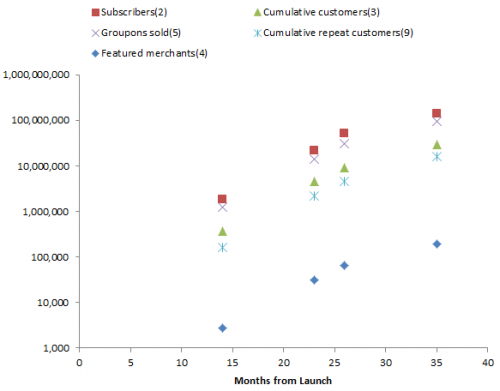 The variable of greatest interest with respect to revenue is Groupons sold. But the others also play a role in determining costs – it takes money to acquire and retain customers. Also, there are actually two populations growing logistically – users and merchants. Growth is presumably a function of the interaction between these two populations. The attractiveness of Groupon to customers depends on having good deals on offer, and the attractiveness to merchants depends on having a large customer pool.
The variable of greatest interest with respect to revenue is Groupons sold. But the others also play a role in determining costs – it takes money to acquire and retain customers. Also, there are actually two populations growing logistically – users and merchants. Growth is presumably a function of the interaction between these two populations. The attractiveness of Groupon to customers depends on having good deals on offer, and the attractiveness to merchants depends on having a large customer pool.