Tag: behavior

Vonnegut does the reference modes of stories

Via NPR,

All of us, even if we have no knack for science, look at the weather, at our children, at our markets, at the sky, and we see rhythms and patterns that seem to repeat, that give us the ability to predict. …

Do any of us live beyond pattern? …

I don’t think so. Artists may be, oddly, the most pattern-aware. Case in point: The totally unpredictable, one-of-a-kind novelist Kurt Vonnegut … once gave a lecture in which he presented — in graphic form — the basic plots of all the world’s great stories. Every story you’ve ever heard, he said, are reflections of a few, classic story shapes. They are so elementary, he said, he could draw them on an X/Y axis.

Systems thinkers, watch for:

  • one big reference mode diagram
  • quantification without measurement
  • a discrete event, modeled with finite slope

The Secret of the Universe in 6 sentences

Niall Palfreyman wrote this on the board to introduce a course in differential equations:

  1. The Secret of the Universe in 6 sentences
  2. Nature always integrates flows over time
  3. Flows always differentiate fields over space
  4. Structure determines behaviour
  5. Algebra is the study of structure
  6. Dynamics is the study of behaviour

I like it.

A little explanation is in order. I have my morning coffee in hand. It’s warmer than the room, so it’s cooling off. It’s heat winds up in the room. If I want to manage my coffee well, neither burning my tongue nor gagging down cold sludge, I need to be able to make some predictions about the future behavior of my cuppa joe. I won’t get far by postulating demons randomly stealing calorics from my cup, though that might provide a soothingly fatalistic outlook. I’m much better off if I understand how and why coffee cools.

#2, the “nature integrates flows” part of the system looks like this:

coffeeCooling

Each box represents an accumulation of heat (that’s the integral). Each pipe represents a flow of heat from one place to another. The heat currently in the house is simply the net result of all the inflows from coffee cups, and all the losses to the outside world, over all time (of course, there are other flows to consider, like my computers warming the room, and losses to the snowy outside).

In the same way, the number of people in a room is the net accumulation of all the people who ever entered, less all those who ever left. A neat thing about this is that the current heat in the cup, or count of people in a room, is a complete description of the state of the system. You don’t need to know the detailed history of inflows and outflows, because you can simply take the temperature of the cup or count the people in the room to measure the accumulated effects of all the past events.

The next question is, why does the heat flow? That’s what #3 is about. Heat follows temperature gradients, as water flows downhill. Here’s a temperature field for a coffee cup:

Coffee_applepie_infrared

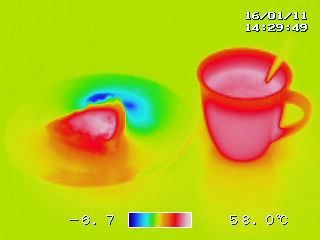
wikimedia commons

Heat will flow from the hot (red) cup into the cool (green) environment. The flow will be fastest where the gradient is steepest – i.e. where there’s the greatest temperature difference over a unit of space. That’s the “flows differentiate fields” part. Other properties also matter, like the thermal conductivity of the cup, air currents in the room, insulation in the wall, and heat capacity of coffee, and these can also be described as distributions over space or fields. That adds the blue to the model above:

CoffeeStructure

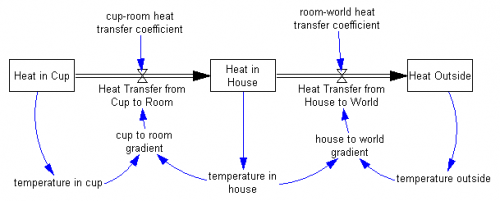
The blue arrows describe why the flows flow. These are algebraic expressions, like Heat Transfer from Cup to Room = Cup to Room Gradient/Cup-Room Heat Transfer Coefficient. They describe the structure – the “why” – of the system (#5).

The behavior of the system, i.e. how fast my coffee cools, is determined by the structure described above (#4). If you change the structure, by using an insulated mug to change the cup-room heat transfer coefficient for example, you change the behavior – the coffee cools more slowly.* The search for understanding about coffee cups, nuclear reactors, and climate is essentially an effort to identify structures that explain the dynamics or patterns of behavior that we observe in the world.

* Update: added a sentence for clarification, and corrected numbering.

Market Growth

John Morecroft’s implementation of Jay Forrester’s Market Growth model, replicated by an MIT colleague whose name is lost to the mists of time, from:

Morecroft, J. D. W. (1983). System Dynamics: Portraying Bounded Rationality. Omega, 11(2), 131-142.

This paper examines the linkages between system dynamics and the Carnegie school in their treatment of human decision making. It is argued that the structure of system dynamics models implicitly assumes bounded rationality in decision making and that recognition of this assumption would aid system dynamicists in model construction and in communication to other social science disciplines. The paper begins by examining Simon’s “Principle of Bounded Rationality” which draws attention to the cognitive limitations on the information gathering and processing powers of human decision makers. Forrester’s “Market Growth Model” is used to illustrate the central theme that system dynamics models are portrayals of bounded rationality. Close examination of the model formulation reveals decision functions involving simple rules of thumb and limited information content. …

Continue reading “Market Growth”

Battle of the Bulb II

The White House has announced new standards for lighting. As I’ve said before, I prefer an economic ban to an outright ban. A less-draconian performance standard may have advantages though. I just visited Erling Moxnes in Norway, who handed me an interesting paper that describes one possible benefit of standards, even where consumers are assumed to optimize.

A frequent argument against efficiency standards is that they prohibit products that represent optimal choices for customers and thus lead to reduced customer utility. In this paper we propose and test a method to estimate such losses. Conjoint analysis is used to estimate utility functions for individuals that have recently bought a refrigerator. The utility functions are used to calculate the individuals’ utility of all the refrigerators available in the market. Revealed utility losses due to non-optimal choices by the customers seem consistent with other data on customer behavior. The same utility estimates are used to find losses due to energy efficiency standards that remove products from the market. Contrary to previous claims, we find that efficiency standards can lead to increased utility for the average customer. This is possible because customers do not make perfect choices in the first place.

The key here is not that customers are stupid and need to be coddled by the government. The method accepts customer utility functions as is (along with possible misperceptions). However, consumers perform limited search for appliances (presumably because search is costly), and thus there’s a significant random component to their choices. Standards help in that case by focusing the search space, at least with respect to one product attribute. They’re even more helpful to the extent that energy efficiency is correlated with other aspects of product quality (e.g., due to use of higher-quality components).

Estimating customer utility of energy efficiency standards for refrigerators. Erling Moxnes. Economic Psychology 25, 707-724. 2004.

Ethics, Equity & Models

I’m at the 2008 Balaton Group meeting, where a unique confluence of modeling talent, philosophy, history, activist know-how, compassion and thirst for sustainability makes it hard to go 5 minutes without having a Big Idea.

Our premeeting tackled Ethics, Values, and the Next Generation of Energy and Climate Modeling. I presented a primer on discounting and welfare in integrated assessment modeling, based on a document I wrote for last year’s meeting, translating some of the issues raised by the Stern Review and critiques into plainer language. Along the way, I kept a running list of assumptions in models and modeling processes that have ethical/equity implications.

There are three broad insights:

  1. Technical choices in models have ethical implications. For example, choices about the representation of technology and resource constraints determine whether a model explores a parameter space where “growing to help the poor” is a good idea or not.
  2. Modelers’ prescriptive and descriptive uses of discounting and other explicit choices with ethical implications are often not clearly distinguished.
  3. Decision makers have no clue how the items above influence model outcomes, and do not in any case operate at that level of description.

My list of ethical issues is long and somewhat overlapping. Perhaps in part that is due to the fact that I compiled it with no clear definition of ‘ethics’ in mind. However, I think it’s also due to the fact that there are inevitably large gray areas in practice, accentuated by the fact that the issue doesn’t receive much formal attention. Here goes: Continue reading “Ethics, Equity & Models”