Sometimes it’s useful to have a way to express a variable as a flexible function of time, so that you can find the trajectory that maximizes some quantity like profit or fit to data. A caveat: this is not generally the best thing to do. A simple feedback rule will be more robust to rescaling and uncertainty and more informative than a function of time. However, there are times when it’s useful for testing or data approximation to have an open-loop decision rule. The attached models illustrate some options.
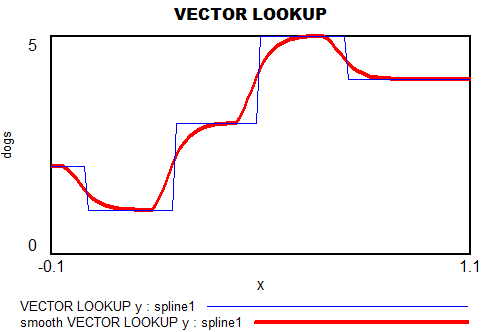
If you have access to arrays in Vensim, the simplest is to use the VECTOR LOOKUP function, which reads a subscripted table of values with interpolation. However, that has two limitations: a uniform time axis, and linear interpolation.
If you want a smooth function, a natural option is to pick a polynomial, like
y = a + b*t + c*t^2 + d*t^3 …
However, it can be a little fiddly to interpret the coefficients or get them to produce a desired behavior. The Legendre polynomials provide a basis with nicer scaling, which still recovers the basic linear, quadratic, cubic (etc.) terms when needed. (In terms of my last post, their improved properties make them less sloppy.)
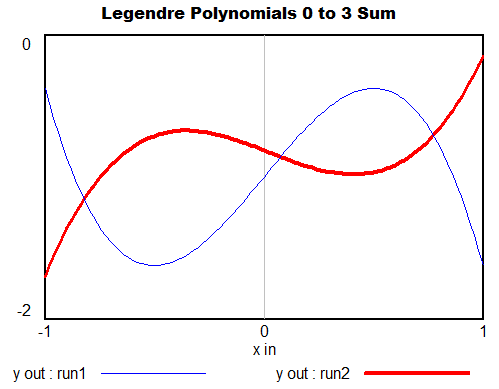
You can generalize these to 2 dimensions by taking tensor products of the 1D series. Another option is to pick the first n terms of Pascal’s triangle. These yield essentially the same result, and either way, things get complex fast.
Back to 1D series, what if you want to express the values as a sequence of x-y points, with smooth interpolation, rather than arcane coefficients? One option is the Lagrange interpolating polynomial. It’s simple to implement, and has continuous derivatives, but it’s an N^2 problem and therefore potentially compute-intensive. It might also behave badly outside its interval, or inside due to ringing.
Probably the best choice for a smooth trajectory specified by x-y points (and optionally, the slope at each point) is a cubic spline or Bezier curve.
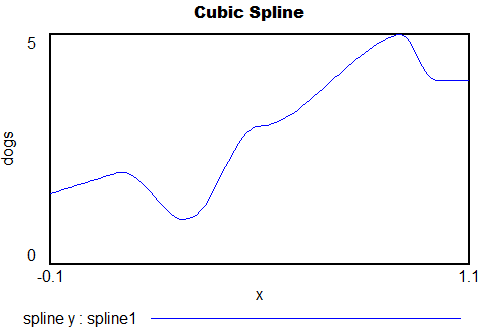
Polynomials1.mdl – simple smooth functions, Legendre, Lagrange and spline, runs in any version of Vensim
InterpolatingArrays.mdl InterpolatingArrays.vpm – array functions, VECTOR LOOKUP, Lagrange and spline, requires Pro/DSS or the free Reader
