December 2024 - MetaSD

Better Documentation

There’s a recent talk by Stefan Rahmstorf that gives a good overview of the tipping point in the AMOC, which has huge implications.

I thought it would be neat to add the Stommel box model to my library, because it’s a nice low-order example of a tipping point. I turned to a recent update of the model by Wei & Zhang in GRL.

It’s an interesting paper, but it turns out that documentation falls short of the standards we like to see in SD, making it a pain to replicate. The good part is that the equations are provided:

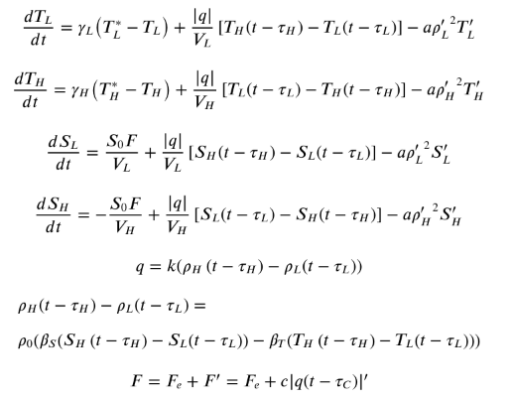The bad news is that the explanation of these terms is brief to the point of absurdity:

This paragraph requires you to maintain a mental stack of no less than 12 items if you want to be able to match the symbols to their explanations. You also have to read carefully if you want to know that ‘ means “anomaly” rather than “derivative”.

The supplemental material does at least include a table of parameters – but it’s incomplete. To find the delay taus, for example, you have to consult the text and figure captions, because they vary. Initial conditions are also not conveniently specified.

I like the terse mathematical description of a system because you can readily take in the entirety of a state variable or even the whole system at a glance. But it’s not enough to check the “we have Greek letters” box. You also need to check the “serious person could reproduce these results in a reasonable amount of time” box.

Code would be a nice complement to the equations, though that comes with it’s own problems: tower-of-Babel language choices and extraneous cruft in the code. In this case, I’d be happy with just a more complete high-level description – at least:

A complete table of parameters and units, with values used in various experiments.
Inclusion of initial conditions for each state variable.
Separation of terms in the RhoH-RhoL equation.

A lot of these issues are things you wouldn’t even know are there until you attempt replication. Unfortunately, that is something reviewers seldom do. But electrons are cheap, so there’s really no reason not to do a more comprehensive documentation job.

Destroying agency competence

Normally, and maybe ideally, provision of government services is managed by a political process that balances enthusiasm for services received against the cost of the taxes required to provide those services (green loops). There are lots of ways this can go wrong, but at present 3 pathologies seem especially prevalent. The driving force behind these is wealth inequality, because it unbalances the benefits of services and the costs. The benefits generally accrue broadly, whereas costs (taxes) fall where the money is (at least in a flat or progressive system). This means that, if you’re wealthy, it’s cheaper to use FedEx than to fund the USPS, and cheaper to move to a place with clean air than to clean up your refinery. This process is shown with heavy lines below.

The oldest pathology this triggers is outright corruption (red loop), by hijacking agency resources for private gain rather than public benefit. I’m thinking of the mysterious award of a $300m contract to restore Puerto Rico’s electric power to a company with 2 employees, coincidentally acquaintances of Interior Secretary Zinke.

While there may not be anything new under the sun, the other two pathologies seem to be ascendant lately. These rely on the fact that you don’t have to steal an agency’s money if your goal is to quit paying for it. If you can’t defeat it politically in an open contest, because a constituency enjoys its services, you can undermine that support by destroying those services (orange loop). This reminds me of destruction of mail sorting machinery and the general degradation of USPS service that has happened under DeJoy’s tenure.

If you can’t destroy the reality of the agency, you can destroy the perception of the agency by attacking its measurement systems. If, for example, the EPA can’t measure air and water quality, or climate, it not only undermines the ability to operate standards and enforcement, it destroys the ability to even perceive the need for these measurements. This is often easy to do, because measurements don’t have direct constituencies, unlike roads or education. This is the first deadly sin of complex system management, and will leave us effectively flying an airplane with a clown car cockpit. Even worse, it makes it easier for the leaders of these misguided efforts to believe their own BS, and get away with it – at least in the short run.

A case for strict unit testing

Over on the Vensim forum, Jean-Jacques Laublé points out an interesting bug in the World3 population sector. His forum post includes the model, with a revealing extreme conditions test and a correction. I think it’s important enough to copy my take here:

This is a very interesting discovery. The equations in question are:
maturation 14 to 15 =
 ( ( Population 0 To 14 ) )
 * ( 1
 - mortality 0 to 14 )
 / 15
 Units: Person/year
 The fractional rate at which people aged 0-14 mature into the
 next age cohort (MAT1#5).

**************************************************************
 mortality 0 to 14=
 IF THEN ELSE(Time = 2020 * one year, 1 / one year, mortality 0 to 14 table
 ( life expectancy/one year ) )
 Units: 1/year
 The fractional mortality rate for people aged 0-14 (M1#4).

**************************************************************
(The second is the one modified for the pulse mortality test.)

In the ‘maturation 14 to 15′ equation, the obvious issue is that ’15’ is a hidden dimensioned parameter. One might argue that this instance is ‘safe’ because 15 years is definitionally the residence time of people in the 0 to 15 cohort – but I would still avoid this usage, and make the 15 yrs a named parameter, like “child cohort duration”, with a corresponding name change to the stock. If nothing else, this would make the structure easier to reuse.

The sneaky bit here, revealed by JJ’s test, is that the ‘1’ in the term (1 – mortality 0 to 14) is not a benign dimensionless number, as we often assume in constructions like 1/(1+a*x). This 1 actually represents the maximum feasible stock outflow rate, in fraction/year, implying that a mortality rate of 1/yr, as in the test input, would consume the entire outflow, leaving no children alive to mature into the next cohort. This is incorrect, because the maximum feasible outflow rate is 1/TIME STEP, and TIME STEP = 0.5, so that 1 should really be 2 ~ frac/year. This is why maturation wrongly goes to 0 in JJ’s experiment, where some children remain to age into the next cohort.

In addition, this construction means that the origin of units in the equation are incorrect – the ’15’ has to be assumed to be dimensionless for this to work. If we assign correct units to the inputs, we have a problem:
maturation 14 to 15 = ~ people/year/year
 ( ( Population 0 To 14 ) ) ~ people
 * ( 1 - mortality 0 to 14 ) ~ fraction/year
 / 15 ~ 1/year
Obviously the left side of this equation, maturation, cannot be people/year/year.

JJ’s correction is:
maturation 14 to 15=
 ( ( Population 0 To 14 ) )
 * ( 1 - (mortality 0 to 14 * TIME STEP))
 / size of the 0 to 14 population
In this case, the ‘1’ represents the maximum fraction of the population that can flow out in a time step, so it really is dimensionless. (mortality 0 to 14 * TIME STEP) represents the fractional outflow from mortality within the time step, so it too is properly dimensionless (1/year * year). You could also write this term as:
( 1/TIME STEP - mortality 0 to 14 ) / (1/TIME STEP)
In this case you can see that the term is reducing maturation by the fraction of cohort residents who don’t make it to the next age group. 1/TIME STEP represents the maximum feasible outflow, i.e. 2/year if TIME STEP = 0.5 year. In this form, it’s easy to see that this term approaches 1 (no effect) in the continuous time limit as TIME STEP approaches 0.

I should add that these issues probably have only a tiny influence on the kind of experiments performed in Limits to Growth and certainly wouldn’t change the qualitative conclusions. However, I think there’s still a strong argument for careful attention to units: a model that’s right for the wrong reasons is a danger to future users (including yourself), who might use it in unanticipated ways that challenge the robustness in extremes.