Category: SystemDynamics

Communicating uncertainty and policy sensitivity

This video is a quick attempt to run through some ways to look at how policy effects are contingent on an uncertain landscape.

I used a simple infection model in Ventity for convenience, though you could do this with many tools.

To paraphrase Mark Twain (or was it …), “If I had more time, I would have made a shorter video.” But that’s really part of the challenge: it’s hard to do a good job of explaining the dynamics of a system contingent on a wide variety of parameter choices in a short time.

One possible response is Forrester’s: we simply can’t teach everything about a nonlinear dynamic system if we have to start from scratch and the listener has a short attention span. So we need to build up systems literacy for the long haul. But I’d be interested in your thoughts on how to pack the essentials into a YouTube short.

Sources of Uncertainty

The confidence bounds I showed in my previous post have some interesting features. The following plots show three sources of the uncertainty in simulated surveillance for Chronic Wasting Disease in deer.

  • Parameter uncertainty
  • Sampling error in the measurement process
  • Driving noise from random interactions in the population

You could add external disturbances like weather to this list, though we don’t simulate it here.

By way of background, this come from a fairly big model that combines the dynamics of the host (deer) with an SIR-like model of disease transmission and progression. There’s quite a bit of disaggregation (regions, ages, sexes). The model is driven by historic harvest and sample sizes, and generates deer population, vegetation, and disease dynamics endogenously. The parameters used here represent a Bayesian posterior, from MCMC with literature priors and a lot of data. The parameter sample from the posterior is a joint distribution that captures both individual parameter variation and covariation (though with only a few exceptions things seem to be relatively independent).

Here’s the effect of parameter uncertainty on the disease trajectory:

Each of the 10,000 runs making up this ensemble is deterministic. It’s surprisingly tight, because it is well-determined by the data.

However, parameter uncertainty is not the only issue. Even if you know the actual state of the disease perfectly, there’s still uncertainty in the reported outcome due to sampling variation. You might stray from the “true” prevalence of the disease because of chance in the selection of which deer are actually tested. Making sampling stochastic broadens the bounds:

That’s still not the whole picture, because deer aren’t really deterministic. They come in integer quanta and they have random interactions. Thus a standard SD formulation like:

births = birth rate * doe population

becomes

births = Poisson( birth rate * doe population )

For stock outflows, like the transition from healthy to infected, the Binomial distribution may be the appropriate choice. This means there’s additional variance around the deterministic course, and the model can explore a wider set of trajectories.

There’s one other interesting feature, particularly evident in this last graph: uncertainty around the mean (i.e. the geometric standard deviation) varies quite a bit. Initially, uncertainty increases with time – as Yogi Berra said, “It’s tough to make predictions, especially about the future.” In the early stages of the disese (2003-2008 say), numbers are small and random events affect the timing of takeoff of the disease, amplified by future positive feedback. A deterministic disease model with reproduction ratio R0>1 can only grow, but in a stochastic model luck can cause the disease to go extinct or bumble around 0 prevalence for a while before emerging into growth. Towards the end of this simulation, the confidence bounds narrow. There are two reasons for this: negative feedback is starting to dominate as the disease approaches saturation prevalence, and at the same time the normalized standard deviation of the sampling errors and randomness in deer dynamics is decreasing as the numbers become larger (essentially with 1/sqrt(n)).

This is not uncommon in real systems. For example, you may be unsure where a chaotic pendulum will be in it’s swing a minute from now. But you can be pretty sure that after an hour or a day it will be hanging idle at dead center. However, this might not remain true when you broaden the boundary of the system to include additional feedbacks or disturbances. In this CWD model, for example, there’s some additional feedback from human behavior (not in the statistical model, but in the full version) that conditions the eventual saturation point, perhaps preventing convergence of uncertainty.

 

Understanding Prediction

I posted my recent blogs on Forrester and forecasting uncertainty over at LinkedIn, and there’s been some good discussion. I want to highlight a few things.

First, a colleague pointed out that the way terms are understood is in the eye of the beholder. When you say “forecast” or “prediction” or “projection” the listener (client, stakeholder) may not hear what you mean. So regardless of whether your intention is correct when you say you’re going to “predict” something, you’d better be sure that your choice of language communicates to the end user with some fidelity.

Second, Samuel Allen asked a great question, which I haven’t answered to my satisfaction, “what are some good ways of preventing consumers of our conditional predictions from misunderstanding them?”

One piece of the puzzle is in Alan Graham’s comment:

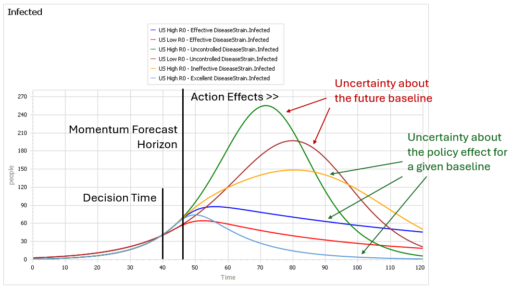
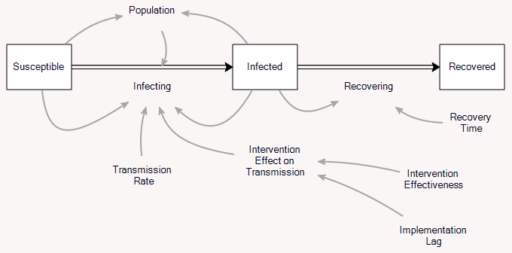
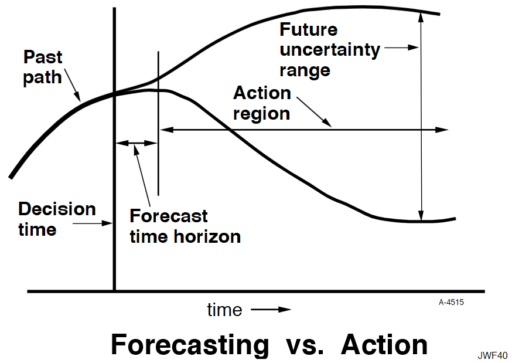
an explanation that has communicated well starts from the distinction between behavior sensitivity (does the simulation change?) versus outcome or policy sensitivity (does the size or direction of the policy impact change?). Two different sets of experiments are needed to answer the two different questions, which are visually distinct:

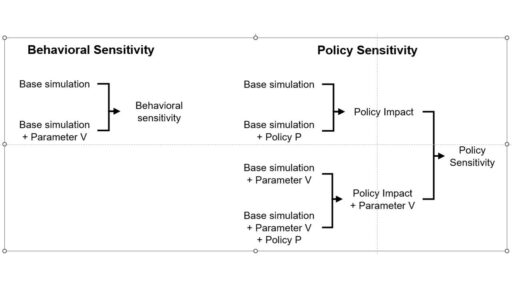
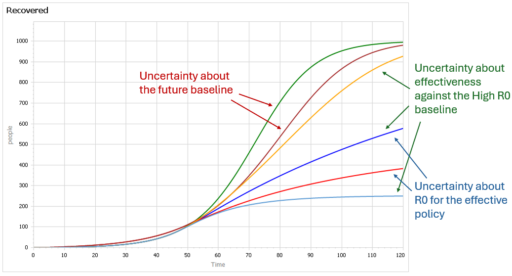
This is basically a cleaner explanation of what’s going on in my post on Forecasting Uncertainty. I think what I did there is too complex (too many competing lines), so I’m going to break it down into simpler parts in a followup.

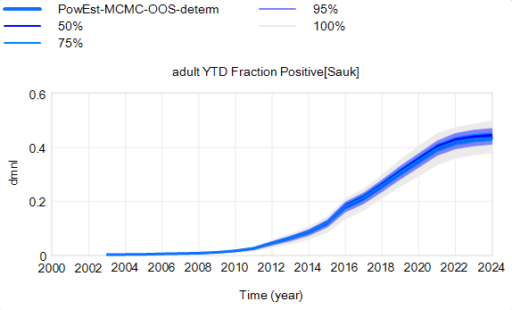
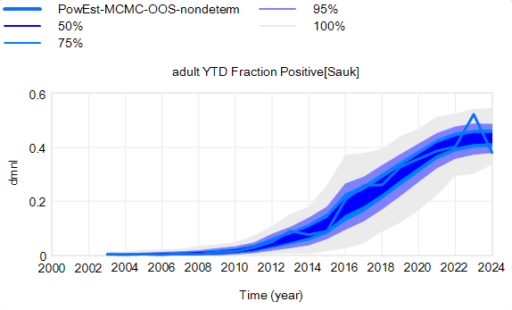
Another piece of the puzzle is visualization. Here’s a pair of scenarios from our CWD model. These are basically nowcasts showing uncertainty about historic conditions, subject to actual historic actions or a counterfactual “high harvest” scenario:

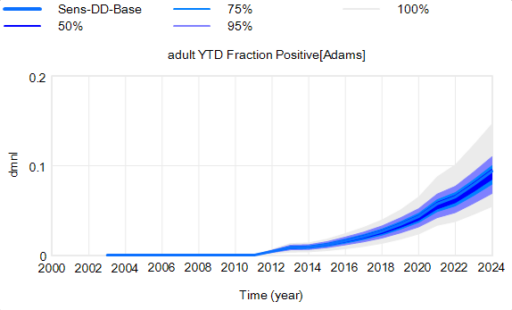
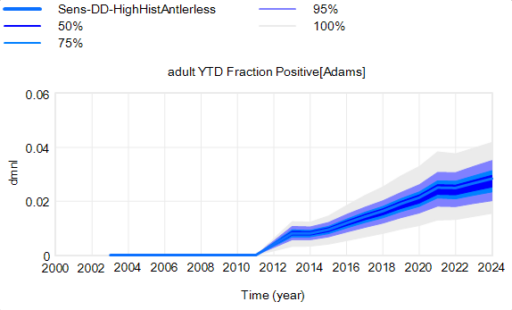Note that I’m just grabbing raw stuff out of Vensim; for presentation these graphics could be cleaner. Also note the different scales.

On each of these charts, the spread indicates uncertainty from parameters and sampling error in disease surveillance. Comparing the two tells you how the behavior – including the uncertainty – is sensitive to the policy change.

In my experience, this works, but it’s cumbersome. There’s just too much information. You can put the two confidence bands on the same chart, using different colors, but then you have fuzzy things overlapping and it’s potentially hard to read.

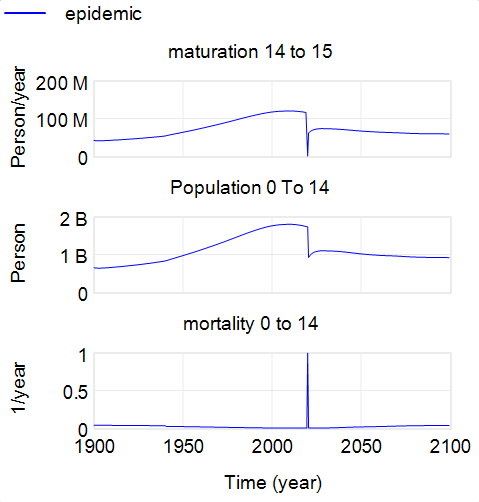
Another option is to use histograms that slice the outcome (here, at the endpoint):

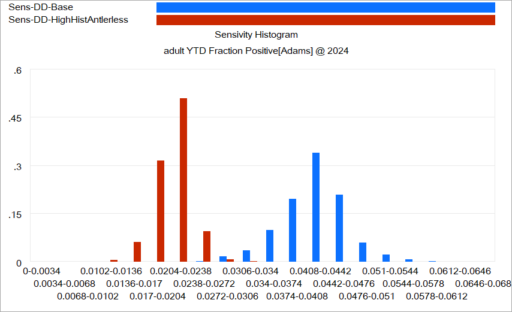Again, this is just a quick capture that could be improved with minimal effort. The spread for each color shows the distribution of possibilities, given the uncertainty from parameters and sampling. The spread between the colors shows the policy impact. You can see that the counterfactual policy (red) both improves the mean outcome (shift left) and reduces the variance (narrower). I actually like this view of things. Unfortunately, I haven’t had much luck with such things in general audiences, who tend to wonder what the axes represent.

I think one answer may be that you simply have to go back to basics and explore the sensitivity of the policy to individual parameter changes, in paired trials per Alan Graham’s diagram above, in order to build understanding of how this works.

I think the challenge of this task – and time required to address it – should not be underestimated. I think there’s often a hope that an SD model can be used to extract an insight about some key leverage point or feedback loop that solves a problem. With the new understanding in hand, the model can be discarded. I can think of some examples where this worked, but they’re mostly simple systems and one-off decisions. In complex situations with a lot of uncertainty, I think it may be necessary to keep the model in the loop. Otherwise, a year down the road, arrival of confounding results is likely to drive people back to erroneous heuristics and unravel the solution.

I’d be interested to hear success stories about communicating model uncertainty.

Forecasting Uncertainty

Here’s an example that illustrates what I think Forrester was talking about.

This is a set of scenarios from a simple SIR epidemic model in Ventity.

There are two sources of uncertainty in this model: the aggressiveness of the disease (transmission rate) and the effectiveness of an NPI policy that reduces transmission.

Early in the epidemic, at time 40 where the decision to intervene is made, it’s hard to tell the difference between a high transmission rate and a lower transmission rate with a slightly larger initial infected population. This is especially true in the real world, because early in an epidemic the information-gathering infrastructure is weak.

However, you can still make decent momentum forecasts by extrapolating from the early returns for a few more days – to time 45 or 50 perhaps. But this is not useful, because that roughly corresponds with the implementation lag for the policy. So, over the period of skilled momentum forecasts, it’s not possible to have much influence.

Beyond time 50, there’s a LOT of uncertainty in the disease trajectory, both from the uncontrolled baseline (is R0 low or high?) and the policy effectiveness (do masks work?). The yellow curve (high R0, low effectiveness) illustrates a key feature of epidemics: a policy that falls short of lowering the reproduction ratio below 1 results in continued growth of infection. It’s still beneficial, but constituents are likely to perceive this as a failure and abandon the policy (returning to the baseline, which is worse).

Some of these features are easier to see by looking at the cumulative outcome. Notice that the point prediction for times after about 60 has extremely large variance. But not everything is uncertain. In the uncontrolled baseline runs (green and brownish), eventually almost everyone gets the disease, it’s a matter of when not if, so uncertainty actually decreases after time 90 or so. Also, even though the absolute outcome varies a lot, the policy always improves on the baseline (at least neglecting cost, as we are here). So, while the forecast for time 100 might be bad, the contingent prediction for the effect of the policy is qualitatively insensitive to the uncertainty.

Reading between the lines: Forrester on forecasting

I’d like to revisit Jay Forrester’s Next 50 Years article, with particular attention to a couple things I think about every day: forecasting and prediction. I previously tackled Forrester’s view on data.

Along with unwise simplification, we also see system dynamics being drawn into attempting what the client wants even when that is unwise or impossible. Of particular note are two kinds of effort—using system dynamics for forecasting, and placing emphasis on a model’s ability to exactly fit historical data.

With regard to forecasting specific future conditions, we face the same barrier that has long plagued econometrics.

Aside from what Forrester is about to discuss, I think there’s also a key difference, as of the time this was written. Econometric models typically employed lots of data and fast computation, but suffered from severe restrictions on functional form (linearity or log-linearity, Normality of distributions, etc.). SD models had essentially unrestricted functional form, particularly with respect to integration and arbitrary nonlinearity, but suffered from insufficient computational power to do everything we would have liked. To some extent, the fields are converging due to loosening of these constraints, in part because the computer under my desk today is now bigger than the fastest supercomputer in the world when I finished my dissertation years ago.

Econometrics has seldom done better in forecasting than would be achieved by naïve extrapolation of past trends. The reasons for that failure also afflict system dynamics. The reasons why forecasting future conditions fail are fundamental in the nature of systems. The following diagram may be somewhat exaggerated, but illustrates my point.

A system variable has a past path leading up to the current decision time. In the short term, the system has continuity and momentum that will keep it from deviating far from an extrapolation of the past. However, random events will cause an expanding future uncertainty range. An effective forecast for conditions at a future time can be made only as far as the forecast time horizon, during which past continuity still prevails. Beyond that horizon, uncertainty is increasingly dominant. However, the forecast is of little value in that short forecast time horizon because a responding decision will be defeated by the very continuity that made the forecast possible. The resulting decision will have its effect only out in the action region when it has had time to pressure the system away from its past trajectory. In other words, one can forecast future conditions in the region where action is not effective, and one can have influence in the region where forecasting is not reliable. You will recall a more complete discussion of this in Appendix K of Industrial Dynamics.

I think Forrester is basically right. However, I think there’s a key qualification. Some things – particularly physical systems – can be forecast quite well, not just because momentum permits extrapolation, but because there is a good understanding of the system. There’s a continuum of forecast skill, between “all models are wrong” and “some models are useful,” and you need to know where you are on that.

Fortunately, your model can tell you about the prospects for forecasting. You can characterize the uncertainty in the model parameters and environmental drivers, generate a distribution of outcomes, and use that to understand where forecasts will begin to fall apart. This is extremely valuable knowledge, and it may be key for implementation. Stakeholders want to know what your intervention is going to do to the system, and if you can’t tell them – with confidence bounds of some sort – they may have no reason to believe your subsequent attributions of success or failure.

In the hallways of SD, I sometimes hear people misconstrue Forrester, to say that “SD doesn’t predict.” This is balderdash. SD is all about prediction. We may not make point predictions of the future state of a system, but we absolutely make predictions about the effects of a policy change, contingent on uncertainties about parameters, structure and external disturbances. If we didn’t do that, what would be the point of the exercise? That’s precisely what JWF is getting at here:

The emphasis on forecasting future events diverts attention from the kind of forecast that system dynamics can reliably make, that is, the forecasting of the kind of continuing effect that an enduring policy change might cause in the behavior of the system. We should not be advising people on the decision they should now make, but rather on how to change policies that will guide future decisions. A properly designed system dynamics model is effective in forecasting how different decision-making policies lead to different kinds of system behavior.

Better Documentation

There’s a recent talk by Stefan Rahmstorf that gives a good overview of the tipping point in the AMOC, which has huge implications.

I thought it would be neat to add the Stommel box model to my library, because it’s a nice low-order example of a tipping point. I turned to a recent update of the model by Wei & Zhang in GRL.

It’s an interesting paper, but it turns out that documentation falls short of the standards we like to see in SD, making it a pain to replicate. The good part is that the equations are provided:

The bad news is that the explanation of these terms is brief to the point of absurdity:

This paragraph requires you to maintain a mental stack of no less than 12 items if you want to be able to match the symbols to their explanations. You also have to read carefully if you want to know that ‘ means “anomaly” rather than “derivative”.

The supplemental material does at least include a table of parameters – but it’s incomplete. To find the delay taus, for example, you have to consult the text and figure captions, because they vary. Initial conditions are also not conveniently specified.

I like the terse mathematical description of a system because you can readily take in the entirety of a state variable or even the whole system at a glance. But it’s not enough to check the “we have Greek letters” box. You also need to check the “serious person could reproduce these results in a reasonable amount of time” box.

Code would be a nice complement to the equations, though that comes with it’s own problems: tower-of-Babel language choices and extraneous cruft in the code. In this case, I’d be happy with just a more complete high-level description – at least:

  • A complete table of parameters and units, with values used in various experiments.
  • Inclusion of initial conditions for each state variable.
  • Separation of terms in the RhoH-RhoL equation.

A lot of these issues are things you wouldn’t even know are there until you attempt replication. Unfortunately, that is something reviewers seldom do. But electrons are cheap, so there’s really no reason not to do a more comprehensive documentation job.

 

A case for strict unit testing

Over on the Vensim forum, Jean-Jacques Laublé points out an interesting bug in the World3 population sector. His forum post includes the model, with a revealing extreme conditions test and a correction. I think it’s important enough to copy my take here:

This is a very interesting discovery. The equations in question are:

maturation 14 to 15 =
 ( ( Population 0 To 14 ) )
 * ( 1
 - mortality 0 to 14 )
 / 15
 Units: Person/year
 The fractional rate at which people aged 0-14 mature into the
 next age cohort (MAT1#5).

**************************************************************
 mortality 0 to 14=
 IF THEN ELSE(Time = 2020 * one year, 1 / one year, mortality 0 to 14 table
 ( life expectancy/one year ) )
 Units: 1/year
 The fractional mortality rate for people aged 0-14 (M1#4).

**************************************************************

(The second is the one modified for the pulse mortality test.)

In the ‘maturation 14 to 15′ equation, the obvious issue is that ’15’ is a hidden dimensioned parameter. One might argue that this instance is ‘safe’ because 15 years is definitionally the residence time of people in the 0 to 15 cohort – but I would still avoid this usage, and make the 15 yrs a named parameter, like “child cohort duration”, with a corresponding name change to the stock. If nothing else, this would make the structure easier to reuse.

The sneaky bit here, revealed by JJ’s test, is that the ‘1’ in the term (1 – mortality 0 to 14) is not a benign dimensionless number, as we often assume in constructions like 1/(1+a*x). This 1 actually represents the maximum feasible stock outflow rate, in fraction/year, implying that a mortality rate of 1/yr, as in the test input, would consume the entire outflow, leaving no children alive to mature into the next cohort. This is incorrect, because the maximum feasible outflow rate is 1/TIME STEP, and TIME STEP = 0.5, so that 1 should really be 2 ~ frac/year. This is why maturation wrongly goes to 0 in JJ’s experiment, where some children remain to age into the next cohort.

In addition, this construction means that the origin of units in the equation are incorrect – the ’15’ has to be assumed to be dimensionless for this to work. If we assign correct units to the inputs, we have a problem:

maturation 14 to 15 = ~ people/year/year
 ( ( Population 0 To 14 ) ) ~ people
 * ( 1 - mortality 0 to 14 ) ~ fraction/year
 / 15 ~ 1/year

Obviously the left side of this equation, maturation, cannot be people/year/year.

JJ’s correction is:

maturation 14 to 15=
 ( ( Population 0 To 14 ) )
 * ( 1 - (mortality 0 to 14 * TIME STEP))
 / size of the 0 to 14 population

In this case, the ‘1’ represents the maximum fraction of the population that can flow out in a time step, so it really is dimensionless. (mortality 0 to 14 * TIME STEP) represents the fractional outflow from mortality within the time step, so it too is properly dimensionless (1/year * year). You could also write this term as:

( 1/TIME STEP - mortality 0 to 14 ) / (1/TIME STEP)

In this case you can see that the term is reducing maturation by the fraction of cohort residents who don’t make it to the next age group. 1/TIME STEP represents the maximum feasible outflow, i.e. 2/year if TIME STEP = 0.5 year. In this form, it’s easy to see that this term approaches 1 (no effect) in the continuous time limit as TIME STEP approaches 0.

I should add that these issues probably have only a tiny influence on the kind of experiments performed in Limits to Growth and certainly wouldn’t change the qualitative conclusions. However, I think there’s still a strong argument for careful attention to units: a model that’s right for the wrong reasons is a danger to future users (including yourself), who might use it in unanticipated ways that challenge the robustness in extremes.

Just Say No to Complex Equations

Found in an old version of a project model:

IF THEN ELSE( First Time Work Flow[i,Proj,stage
] * TIME STEP >= ( Perceived First Time Scope UEC Work
[i,Proj,uec] + Unstarted Work[i,Proj,stage] )
:OR: Task Is Active[i,Proj,Workstage] = 0
:OR: avg density of OOS work[i,Proj,stage] > OOS density threshold,
Completed work still out of sequence[i,Proj,stage] / TIME STEP
+ new work out of sequence[i,Proj,stage] ,
MIN( Completed work still out of sequence[i,Proj,stage] / Minimum Time to Retrofit Prerequisites into OOS Work
+ new work out of sequence[i,Proj,stage],
new work in sequence[i,Proj,stage]
* ZIDZ( avg density of OOS work[i,Proj,stage],
1 – avg density of OOS work[i,Proj,stage] ) ) )

An equation like this needs to be broken into at least 3 or 4 human-readable chunks. In reviewing papers for the SD conference, I see similar constructions more often than I’d like.

Defining SD

Open Access Note by Asmeret Naugle, Saeed Langarudi, Timothy Clancy: https://doi.org/10.1002/sdr.1762

Abstract
A clear definition of system dynamics modeling can provide shared understanding and clarify the impact of the field. We introduce a set of characteristics that define quantitative system dynamics, selected to capture core philosophy, describe theoretical and practical principles, and apply to historical work but be flexible enough to remain relevant as the field progresses. The defining characteristics are: (1) models are based on causal feedback structure, (2) accumulations and delays are foundational, (3) models are equation-based, (4) concept of time is continuous, and (5) analysis focuses on feedback dynamics. We discuss the implications of these principles and use them to identify research opportunities in which the system dynamics field can advance. These research opportunities include causality, disaggregation, data science and AI, and contributing to scientific advancement. Progress in these areas has the potential to improve both the science and practice of system dynamics.

I shared some earlier thoughts here, but my refined view is in the SDR now:


Invited Commentaries by Tom Fiddaman, Josephine Kaviti Musango, Markus Schwaninger, Miriam Spano: https://doi.org/10.1002/sdr.1763