Category: health

Forecasting Uncertainty

Here’s an example that illustrates what I think Forrester was talking about.

This is a set of scenarios from a simple SIR epidemic model in Ventity.

There are two sources of uncertainty in this model: the aggressiveness of the disease (transmission rate) and the effectiveness of an NPI policy that reduces transmission.

Early in the epidemic, at time 40 where the decision to intervene is made, it’s hard to tell the difference between a high transmission rate and a lower transmission rate with a slightly larger initial infected population. This is especially true in the real world, because early in an epidemic the information-gathering infrastructure is weak.

However, you can still make decent momentum forecasts by extrapolating from the early returns for a few more days – to time 45 or 50 perhaps. But this is not useful, because that roughly corresponds with the implementation lag for the policy. So, over the period of skilled momentum forecasts, it’s not possible to have much influence.

Beyond time 50, there’s a LOT of uncertainty in the disease trajectory, both from the uncontrolled baseline (is R0 low or high?) and the policy effectiveness (do masks work?). The yellow curve (high R0, low effectiveness) illustrates a key feature of epidemics: a policy that falls short of lowering the reproduction ratio below 1 results in continued growth of infection. It’s still beneficial, but constituents are likely to perceive this as a failure and abandon the policy (returning to the baseline, which is worse).

Some of these features are easier to see by looking at the cumulative outcome. Notice that the point prediction for times after about 60 has extremely large variance. But not everything is uncertain. In the uncontrolled baseline runs (green and brownish), eventually almost everyone gets the disease, it’s a matter of when not if, so uncertainty actually decreases after time 90 or so. Also, even though the absolute outcome varies a lot, the policy always improves on the baseline (at least neglecting cost, as we are here). So, while the forecast for time 100 might be bad, the contingent prediction for the effect of the policy is qualitatively insensitive to the uncertainty.

Health Payer-Provider Escalation and its Side Effects

I was at the doctor’s office for a routine checkup recently – except that it’s not a checkup anymore, it’s a “wellness visit”. Just to underscore that, there’s a sign on the front door, stating that you can’t talk to the doctor about any illnesses. So basically you can’t talk to your doctor if you’re sick. Let the insanity of that sink in. Why? Probably because an actual illness would take more time than your insurance would pay for. It’s not just my doc – I’ve seen this kind of thing in several offices.

To my eyes, US health care is getting worse, and its pathologies are much more noticeable. I think consolidation is a big part of the problem. In many places, the effective number of competing firms on both the provider side is 1 or 2, and the number of payers is 2 or 3. I roughly sketched out the effects of this as follows:

The central problem is that the few payers and providers left are in a war of escalation with each other. I suspected that it started with the payers’ systematic denial of, or underpayment for, procedure claims. The providers respond by increasing the complexity of their billing, so they can extract every penny. This creates loops R1 and R2.

Then there’s a side effect: as billing complexity and arbitrary denials increase, small providers lack the economies of scale to fight the payer bureaucracy; eventually they have to fold and accept a buyout from a hospital network (R3). The payers have now shot themselves in the foot, because they’re up against a bigger adversary.

But the payers also benefit from this complexity, because transparency becomes so bad that consumers can no longer tell what they’re paying for, and are more likely to overpay for insurance and copays (R7). This too comes with a cost for the payers though, because consumers no longer contribute to cost control (R6).

As this goes on, consumers no longer have choices, because self-insuring becomes infeasible (R5) – there’s nowhere to shop around (R4) and providers (more concentrated due to R3) overcharge the unlucky to compensate for their losses on covered care. The fixed costs of fighting the system are too high for an individual.

I don’t endorse what Luigi did – it was immoral and ineffective – but I absolutely understand why this system produces rage, violence and the worst bang-for-the-buck in the world.

The insidious thing about the escalating complexity of this system (R1 and R2 again) is that it makes it unfixable. Neither the payers nor the providers can unilaterally arrest this behavior. Nor does tinkering with the rules (as in the ACA) lead to a solution. I don’t know what the right prescription is, but it will have to be something fairly radical: adversaries will have to come together and figure out ways to deliver some real value to consumers, which flies in the face of boardroom pressures for results next quarter.

I will be surprised if the incoming administration dares to wade into this mess without a plan. De-escalating conflict to the benefit of the public is not their forte, nor is grappling with complex systems. Therefore I expect healthcare oligarchy to get worse. I’m not sure what to prescribe other than to proactively do everything you can to stay out of this dysfunctional system.

Meta thought: I think the CLD above captures some of the issues, but like most CLDs, it’s underspecified (and probably misspecified), and it can’t be formally tested. You’d need a formal model to straighten things out, but that’s tricky too: you don’t want a model that includes all the complexity of the current system, because that’s electronic concrete. You need a modestly complex model of the current system and alternatives, so you can use it to figure out how to rewrite the system.

Thyroid Dynamics: Hyper Resurgence

In my last thyroid post, I described a classic case of overshoot due to failure to account for delays. I forgot to mention the trigger for this episode.

At point B above, there was a low TSH measurement, at .05 well below the recommended floor of .4. That was taken as a signal for a dose reduction, which is qualitatively reasonable.

Let’s suppose we believe the dose-TSH response to be stable:

Then we have some puzzles. First, at 200mcg, we’d expect TSH=.15, about 3x higher. To get the observed measurement, we’d expect the dose to be more like 225mcg. Second, exactly the same reading of .05 has been observed at a much lower dose (162.5mcg), which is in the sweet spot (yellow box) we should be targeting. Third, also within that sweet spot, at 150mcg, we’ve seen TSH as high as 15 – far out of range in the opposite direction.

I think an obvious conclusion is that noise in the system is extreme, so there’s good reason to respond by discounting the measurement and retesting. But that’s not what happens in general. Here’s a plot of TSH observations (x, log scale) against subsequent dose adjustments (y, %):
There are three clusters of note.

  • The yellow-highlighted points are low TSH values that were followed by large dose reductions, exceeding guidelines.
  • The green points are large dose increases needed to restore the yellow changes, when they subsequently proved to be errors.
  • The purple points (3 total) are high TSH readings, right at the top of the recommended range, that did not induce a dose increase, even though they were accompanied by symptom complaints.

This is interesting, because the trendline seems to indicate a reasonable, if noisy, strategy of targeting TSH=1. But the operative decision rule for several of the doctors involved seems to be more like:

  • If you get a TSH measurement at the high end of the range, indicating a dose increase might be appropriate, ignore it.
  • If you get a low TSH measurement, PANIC. Cut dose drastically.
  • If you’re the doctor replacing the one just fired for screwing this up, restore the status quo.

Why is this? I think it’s an error in reasoning. Low TSH could be caused by excessive T4 levels, which could arise from (a) overtreatment of a hypothyroid patient, or (b) hyperthyroid activity in a previously hypothyroid patient. In the case described previously, evidence from T4 testing as well as the long term relationship suggested that the dose was 20-30% high, but it was ultimately reduced by 60%. But in two other cases, there was no T4 confirmation, and the dose was right in the middle of its apparent sweet spot. That rules out overtreatment, so the mental model behind a dose reduction has to be (b). But that makes no sense. It’s a negative feedback system, yet somehow the thyroid has increased its activity, in response to a reduction in the hormone that normally signals it to do so? Admittedly, there are possibilities like cancer that could explain such behavior, but no one has ever explored that possibility in N=1’s case.

I think the basic problem here is that it’s hard to keep a mechanistic model of a complex hormone signalling system in your head, which makes it easy to get fooled by delays, feedback, noise and nonlinearity. Bad information systems and TSH monomania contribute to the problem, as does ignoring dose guidelines due to overconfidence.

So what should happen in response to a low TSH measurement in patient N=1? I think it’s more like the following:

  • Don’t panic.
    • It might be a bad measurement (labs don’t correct for seasonality, time of day, and other features that could inflate variance beyond the precision of the test itself).
    • It might be some unknown source of variability driving TSH, like food, medications, or endogenous variation in upstream hormones.
  • Look at the measurement in context of other information: the past dose-response relationship, T4, and symptoms, and reference dose per unit body mass.
  • Make at most a small move, wait for the guideline-prescribed period, and retest.

Thyroid Dynamics: Dose Management Challenges

In my last two posts about thyroid dynamics, I described two key features of the information environment that set up a perfect storm for dose management:

  1. The primary indicator of the system state for a hypothyroid patient is TSH, which has a nonlinear (exponential) response to T3 and T4. This means you need to think about TSH on a log scale, but test results are normally presented on a linear scale. Information about the distribution is hard to come by. (I didn’t mention it before, but there’s also an element of the Titanic steering problem, because TSH moves in a direction opposite the dose and T3/T4.)
  2. Measurements of TSH are subject to a rather extreme mix of measurement error and driving noise (probably mostly the latter). Test results are generally presented without any indication of uncertainty, and doctors generally have very few data points to work with.

As if that weren’t enough, the physics of the system is tricky. A change in dose is reflected in T4 and T3, then in TSH, only after a delay. This is a classic “delayed negative feedback loop” situation, much like the EPO-anemia management challenge in the excellent work by Jim Rogers, Ed Gallaher & David Dingli.

If you have a model, like Rogers et al. do, you can make fairly rapid adjustments with confidence. If you don’t, you need to approach the problem like an unfamiliar shower: make small, slow adjustments. If you react two quickly, you’ll excite oscillations. Dose titration guidelines typically reflects this:

Titrate dosage by 12.5 to 25 mcg increments every 4 to 6 weeks, as needed until the patient is euthyroid.

Just how long should you wait before making a move? That’s actually a little hard to work out from the literature. I asked OpenEvidence about this, and the response was typically vague:

The expected time delay between adjusting the thyroid replacement dose and the response of thyroid-stimulating hormone (TSH) is typically around 4 to 6 weeks. This is based on the half-life of levothyroxine (LT4), which reaches steady-state levels by then, and serum TSH, which reaches its nadir at the same time.[1]

The first citation is the ATA guidelines, but when you consult the details, there’s no cited basis for the 4-6 weeks. Presumably this is some kind of 3-tau rule of thumb learned from experience. As an alternative, I tested a dose change in the Eisenberg et al. model:

At the arrow, I double the synthetic T4 dose on a hypothetical person, then observe the TSH trajectory. Normally, you could then estimate the time constant directly from the chart: 70% of the adjustment is realized at 1*tau, 85% at 2*tau, 95% at 3*tau. If you do that here, tau is about 8 days. But not so fast! TSH responds exponentially, so you need to look at this on a log-y scale:


Looking at this correctly, tau is somewhat longer: about 12-13 days. This is still potentially tricky, because the Eisenberg model is not first order. However, it’s reassuring that I get similar time constants when I estimate my own low-order metamodel.

Taking this result at face value, one could roughly say that TSH is 95% equilibrated to a dose change after about 5 weeks, which corresponds pretty well with the ATA guidelines.


This is a long setup for … the big mistake. Referring to the lettered episodes on the chart above, here’s what happened.

  • A: Dose is constant at about 200mcg (a little hard to be sure, because it was a mix of 2 products, and the equivalents aren’t well established.
  • B: New doctor orders a test, which comes out very low (.05), out of the recommended range. Given the long term dose-response range, we’d expect about .15 at this dose, so it seems likely that this was a confluence of dose-related factors and noise.
  • C: New doc orders an immediate drastic reduction of dose by 37.5% or 75mcg (3 to 6 times the ATA recommended adjustment).
  • D: Day 14 from dose change, retest is still low (.2). At this point you’d expect that TSH is at most 2/3 equilibrated to the new dose. Over extremely vociferous objections, doc orders another 30% reduction to 88mcg.
  • E: Patient feeling bad, experiencing hair loss and other symptoms. Goes off the reservation and uses remaining 125mcg pills. Coincident test is in range, though one would not expect it to remain so, because the dose changes are not equilibrated.
  • F: Suffering a variety of hypothyroid symptoms at the lower dose.
  • G: Retest after an appropriate long interval is far out of range on the high side (TSH near 7). Doc unresponsive.
  • H: Fired the doc. New doc restores dose to 125mcg immediately.
  • I: After an appropriate interval, retest puts TSH at 3.4, on the high side of the ATA range and above the NACB guideline. Doc adjusts to 175mcg, in part considering symptoms rather than test results.

This is an absolutely classic case of overshooting a goal in a delayed negative feedback system. There are really two problems here: failure to anticipate the delay, and therefore making a second adjustment before the first was stabilized, and making overly aggressive changes, much larger than guidelines recommend.

So, what’s really going on? I’ve been working with a simplified meta version of the Eisenberg model to figure this out. (The full model is hourly, and therefore impractical to run with Kalman filtering over multi-year horizons. It’s silly to use that much computation on a dozen data points.)

The problem is, the model can’t replicate the data without invoking huge driving noise – there simply isn’t any thing in the structure that can account for data points far from the median behavior. I’ve highlighted a few above. At each of these points, the model takes a huge jump, not because of any known dynamics, but because of a filter reset of the model state. This is a strong hint that there’s an unobserved state influencing the system.

If we could get docs to provide a retest at these outlier points, we could at least rule out measurement error, but that has almost never happened. Also, if docs would routinely order a full panel including T3 and T4, not just TSH, we might have a better mechanistic explanation, but that has also been hard to get. Recently, a doc ordered a full panel, but office staff unilaterally reduced the scope to TSH only, because they felt that testing T3 and T4 was “unconventional”. No doubt this is because ATA and some authors have been shouting that TSH is the only metric needed, and any nuances that arise when the evidence contradicts get lost.

For our N=1, the instability of the TSH/T4 relationship contradicts the conventional wisdom, which is that individuals have a stable set point., with the observed high population variation arising from diversity of set points across individuals:

I think the obvious explanation in our N=1 is that some individuals have an unstable set point. You could visualize that in the figure above as moving from one intersection of curves to another. This could arise from a change in the T4->TSH curve (e.g. something upstream of TSH in the hypothalamic-pituitary-adrenal axis) or the TSH->T4 relationship (intermittent secretion or conversion). Unfortunately very few treatment guidelines recognize this possibility.

Thyroid Dynamics: Chartjunk

I just ran across a funny instance of TSH nonlinearity. Check out the axis on this chart:

It’s actually not as bad as you’d think: the irregular axis is actually a decent approximation of a log-linear scale:

My main gripe is that the perceptual midpoint of the ATA range bar on the chart is roughly 0.9, whereas the true logarithmic midpoint is more like 1.6. The NACB bar is similarly distorted.

Thyroid Dynamics: Noise

A couple weeks ago I wrote about the perceptual challenges of managing thyroid stimulating hormone (TSH), which has an exponential response to the circulating thyroid hormones (T3 & T4) you’d actually like to control.

Another facet of the thyroid control problem is noise. Generally, uncertainty in measurements is not made available to users. For example, the lab results reported by MyChart have no confidence bounds: If you start looking for information on these tests, you’ll usually find precision estimates that sound pretty good – typically 5 to 7% error. (Example.) However, this understates the severity of the problem.

It’s well known that individual variation in the TSH<->T3,T4 setpoint is large, and the ATA guidelines mention this, if you read the detailed discussion. However, this is presented as a reason for the superiority of TSH measurements, “The logarithmic relationship between TSH and thyroid hormone bestows sensitivity: even if circulating T3 and T4 are in the normal range, it cannot be assumed that the subject is euthyroid. The interindividual ranges for T3 and T4 are much broader than the individual variance (), such that measuring T3 and T4 is a suboptimal way to assess thyroid status.” The control implications of variation over time within an individual are not mentioned.

The issue we face in our N=1 sample is unexplained longitudinal variation around the setpoint. In our data, this is HUGE. At a given dose, even during a long period of stability, variation in TSH is not 10%; it’s a factor of 10.

Now consider the problem facing a doc trying to titrate your dose in a 30-minute visit. They tested your TSH, and it’s 4, or .4, right at the high or low end o the recommended range. Should they adjust the dose? (The doc’s problem is actually harder than the data presented above suggests, because they never see this much data – changes in providers, labs and systems truncate the available information to just a few points.) In our experience, 3 out of 5 doctors do change the dose, even though the confidence bounds on these measurements are probably big enough to sail the Exxon Valdez through.

There is at last a paper that tackles this issue:

Individuals exhibit fluctuations in the concentration of serum thyroid-stimulating hormone (TSH) over time. The scale of these variations ranges from minutes to hours, and from months to years. The main factors contributing to the observed within-person fluctuations in serum TSH comprise pulsatile secretion, circadian rhythm, seasonality, and ageing.

I think the right response is actually the byline of this blog: don’t just do something, stand there! If one measurement potentially has enormous variation, the first thing you should probably do is leave the dose alone and retest after a modest time. On several occasions, we have literally begged for such a retest, and been denied.

The consequence of test aversion is that we have only 20 data points over 8 years, and almost none in close proximity to one another. That makes it impossible to determine whether the variation we’re seeing is measurement error (blood draw or lab methods), fast driving noise (circadian effects), or slow trends (e.g., seasonal). I’ve been fitting models to the data for several years, but this sparsity and uncertainty gives the model fits. Here’s an example:

At the highlighted point (and half a dozen others), the model finds the data completely inexplicable. The Kalman filter moves the model dramatically towards the data (the downward spike in the red curve), but only about halfway, because the estimate yields both high measurement error and high driving noise in TSH. Because the next measurement doesn’t occur for 4 months, there’s no way to sort out which is which.

This extreme noise, plus nonlinearity previously mentioned, is really a perfect setup for errors in dose management. I’ll describe one or two in a future post.

Thyroid Dynamics: Misperceptions of Nonlinearity

I’ve been working on thyroid dynamics, tracking a friend’s data and seeking some understanding with models. With only one patient to go on, it’s impossible to generalize about thyroid behavior from one time series (though there are some interesting features I’ll report on later). On the other hand, our sample size of doctors is now around 10, and I’m starting to see some persistent misperceptions leading to potentially dangerous errors. One of the big issues is simple.

The principal indicator used for thyroid diagnosis is TSH (thyroid stimulating hormone). TSH regulates production of T4 and T3, T3 being the metabolically active hormone. T4 and T3 in turn downregulate TSH (via TRH), producing a negative feedback loop. The basis for the target range for TSH in thyroid treatment is basically the distribution of TSH in the general population without a thyroid diagnosis.

The challenge with TSH is that its response is logarithmic, so its distribution is lognormal. The usual target range is 0.4 to 4 mIU/L (or .45 to 4.5, or something else, depending on which source you prefer). Anyway, suppose you test at 2.2 – bingo! right in the middle! Well, not so fast. The geometric mean of .4 and 4.4 is actually 1.6, so you’re a little high.

How high? Well, no one will tell you without a fight. For some reason, most sources insist on throwing out much of the relevant information about the distribution of “normal”. In fact, when you look at the large survey papers reporting on population health, like NHANES, it’s hard to find the distribution. For example, Thyroid Profile of the Reference United States Population: Data from NHANES 2007-2012 (Jain 2015) doesn’t have a single visualization of the data – just a bunch of tables. When you do find the distribution, you’ll often get a subset (smokers) or a linear-scaled version that makes it hard to see the left tail. (For the record, TSH=2.2 is just above the 75th percentile in the NHANES THYROD_G dataset – so already quite far from the middle.)

There are also more subtle issues. In the first NHANES thyroid survey article, I found Fig. 1:

Here we have a log scale, but bins of convenience. The breakpoints 1, 2, 3, 5, 10… happen to be roughly equally spaced on a log scale. But when you space histogram bins at these intervals, the bin width is very rough indeed – varying by almost a factor of 2. That means the shape of the distribution is distorted. One of the bins expected to be small is the 2.1-3 range, and you can actually see here that those columns look anomalously low, compared to what you’d expect of a nice bell curve.

That was 20 years ago, but things are no better with modern analytics. If you get a blood test now, your results are likely to be reported to you, and your doc, though a system like MyChart. For TSH, this means you’ll get a range plot with a linear scale:

backed up by a time series with a linear scale:

Notice that the “normal” range doesn’t match the ATA recommendation or any other source I’ve seen. Presumably it’s the lab’s +/- 2 standard deviation range or something like that. That’s bad, because the upper limit – 4.82 – is above every clinical association recommendation I’ve seen. The linear scale squashes all the variation around low values, and exaggerates the high ones.

Given that the information systems for the entire thyroid management enterprise offer biased, low-information displays of TSH stats, I think it’s not surprising that physicians have trouble overcoming the nonlinearity bias. They have hundreds of variables to think about, and can’t possibly be expected to maintain a table of log or Z transformations in their heads. Patients are probably even more baffled by the asymmetry.

It would be simple to remedy this by presenting the information in a way that minimizes the cognitive burden on the viewer. Reporting TSH on a log scale is trivial. Reporting percentiles as a complementary statistic would also be trivial, and percentiles are widely used, so you don’t have to explain them. Setting a target value rather than a target range would encourage driving without bouncing off the guardrails. I hope authors and providers can figure this out.

Believing Exponential Growth

Verghese: You were prescient about the shape of the BA.5 variant and how that might look a couple of months before we saw it. What does your crystal ball show of what we can expect in the United Kingdom and the United States in terms of variants that have not yet emerged?

Pagel: The other thing that strikes me is that people still haven’t understood exponential growth 2.5 years in. With the BA.5 or BA.3 before it, or the first Omicron before that, people say, oh, how did you know? Well, it was doubling every week, and I projected forward. Then in 8 weeks, it’s dominant.

It’s not that hard. It’s just that people don’t believe it. Somehow people think, oh, well, it can’t happen. But what exactly is going to stop it? You have to have a mechanism to stop exponential growth at the moment when enough people have immunity. The moment doesn’t last very long, and then you get these repeated waves.

You have to have a mechanism that will stop it evolving, and I don’t see that. We’re not doing anything different to what we were doing a year ago or 6 months ago. So yes, it’s still evolving. There are still new variants shooting up all the time.

At the moment, none of these look devastating; we probably have at least 6 weeks’ breathing space. But another variant will come because I can’t see that we’re doing anything to stop it.

– Medscape, We Are Failing to Use What We’ve Learned About COVID, Eric J. Topol, MD; Abraham Verghese, MD; Christina Pagel, PhD

Mask Mandates and One Study Syndrome

The evidence base for Montana’s new order promoting parental opt-out from school mask mandates relies heavily on two extremely weak studies.

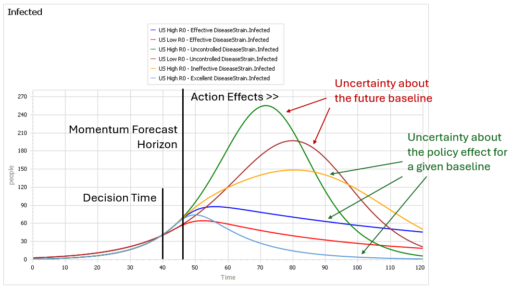
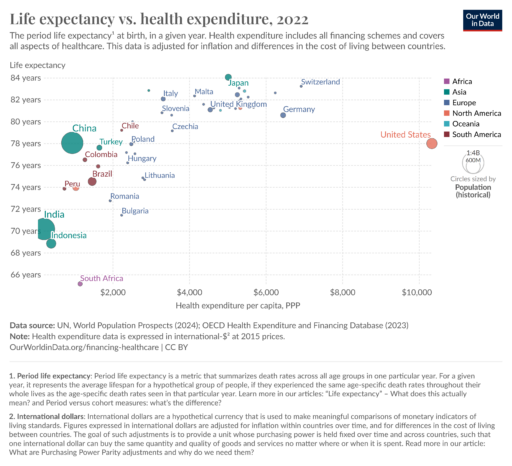
Montana Governor Gianforte just publicized a new DPHHS order requiring schools to provide a parental opt-out for mask requirements.

Underscoring the detrimental impact that universal masking may have on children, the rule cites a body of scientific literature that shows side effects and dangers from prolonged mask wearing.

The order purports to be evidence based. But is the evidence any good?

Mask Efficacy

The order cites:

The scientific literature is not conclusive on the extent of the impact of
masking on reducing the spread of viral infections. The department understands
that randomized control trials have not clearly demonstrated mask efficacy against
respiratory viruses, and observational studies are inconclusive on whether mask use
predicts lower infection rates, especially with respect to children.1

The supporting footnote is basically a dog’s breakfast,

1 See, e.g., Guerra, D. and Guerra, D., Mask mandate and use efficacy for COVID-19 containment in
US States, MedRX, Aug. 7, 2021, https://www.medrxiv.org/content/10.1101/2021.05.18.21257385v2
(“Randomized control trials have not clearly demonstrated mask efficacy against respiratory viruses,
and observational studies conflict on whether mask use predicts lower infection rates.”). Compare
CDC, Science Brief: Community Use of Cloth Masks to Control the Spread of SARS-CoV-2, last
updated May 7, 2021, https://www.cdc.gov/coronavirus/2019-ncov/science/science-briefs/masking-
science-sars-cov2.html, last visited Aug. 30, 2021 (mask wearing reduces new infections, citing
studies) ….

(more stuff of declining quality)

This is not an encouraging start; it’s blatant cherry picking. Guerra & Guerra is an observational statistical test of mask mandates. The statement DPHHS quotes, “Randomized control trials have not clearly demonstrated mask efficacy…” isn’t even part of the study; it’s merely an introductory remark in the abstract.

Much worse, G&G isn’t a “real” model. It’s just a cheap regression of growth rates against mask mandates, with almost no other controls. Specifically, it omits NPIs, weather, prior history of the epidemic in each state, and basically every other interesting covariate, except population density. It’s not even worth critiquing the bathtub statistics issues.

G&G finds no effects of mask mandates. But is that the whole story? No. Among the many covariates they omit is mask compliance. It turns out that matters, as you’d expect. From Leech et al. (one of many better studies DPHHS ignored):

Across these analyses, we find that an entire population wearing masks in public leads to a median reduction in the reproduction number R of 25.8%, with 95% of the medians between 22.2% and 30.9%. In our window of analysis, the median reduction in R associated with the wearing level observed in each region was 20.4% [2.0%, 23.3%]1. We do not find evidence that mandating mask-wearing reduces transmission. Our results suggest that mask-wearing is strongly affected by factors other than mandates.

We establish the effectiveness of mass mask-wearing, and highlight that wearing data, not mandate data, are necessary to infer this effect.

Meanwhile, the DPHHS downplays its second citation, the CDC Science Brief, which cites 65 separate papers, including a number of observational studies that are better than G&G. It concludes that masks work, by a variety of lines of evidence, including mechanistic studies, CFD simulations and laboratory experiments.

Verdict: Relying on a single underpowered, poorly designed regression to make sweeping conclusions about masks is poor practice. In effect, DPHHS has chosen the one earwax-flavored jellybean from a bag of more attractive choices.

Mask Safety

The department order goes on,

The department
understands, however, that there is a body of literature, scientific as well as
survey/anecdotal, on the negative health consequences that some individuals,
especially some children, experience as a result of prolonged mask wearing.2

The footnote refers to Kisielinski et al. – again, a single study in a sea of evidence. At least this time it’s a meta-analysis. But was it done right? I decided to spot check.

K et al. tabulate a variety of claims conveniently in Fig. 2:

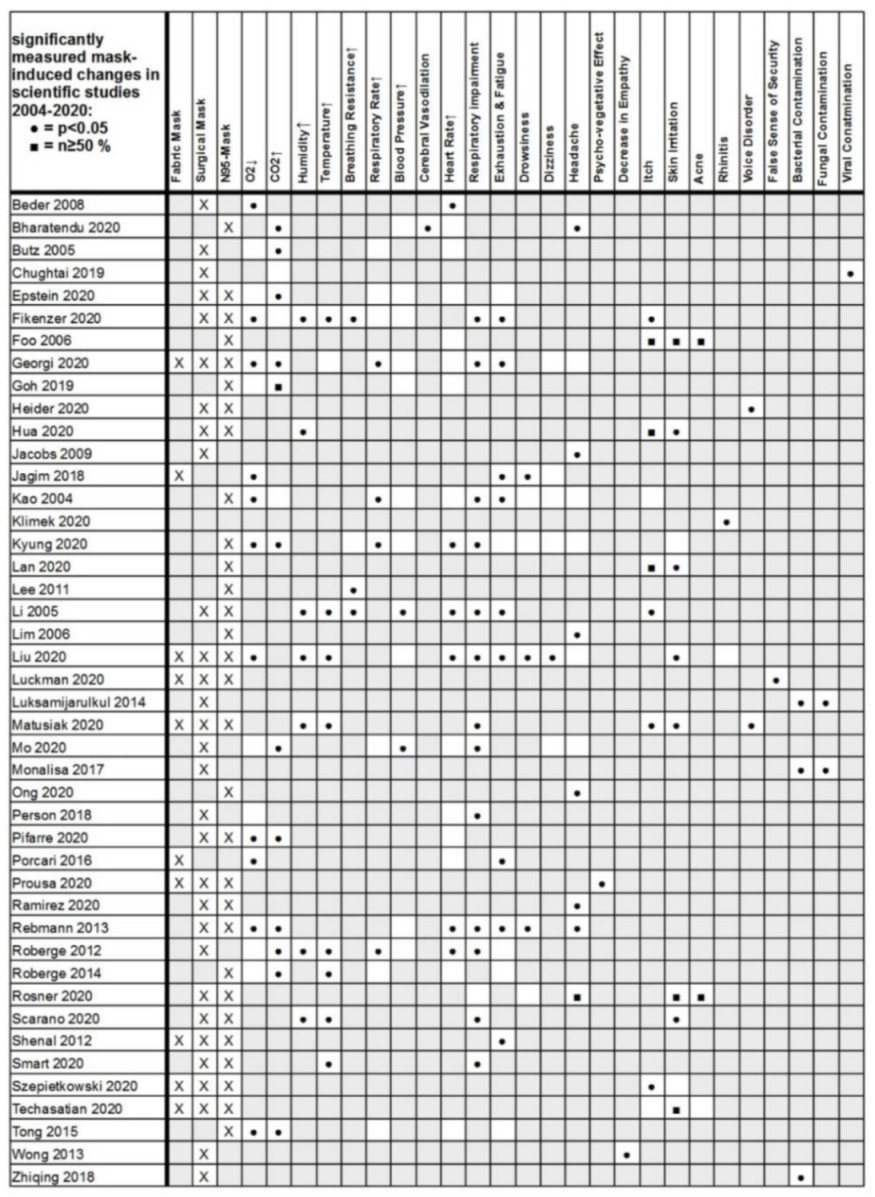
The first claim assessed is that masks reduce O2, so I followed those citations.

Citation Claim Assessment/Notes
Beder 2008 Effect Effect, but you can’t draw any causal conclusion because there’s no control group.
Butz 2005 No effect PhD Thesis, not available for review
Epstein 2020 No effect No effect (during exercise)
Fikenzer 2020 Effect Effect
Georgi 2020 Effect Gray literature, not available for review
Goh 2019 No effect No effect; RCT n~=100 children
Jagim 2018 Effect Not relevant – this concerns a mask designed for elevation training, i.e. deliberately impeding O2
Kao 2004 Effect Effect. End stage renal patients.
Kyung 2020 Effect Dead link. Flaky journal? COPD patients.
Liu 2020 Effect Small effect – <1% SpO2. Nonmedical conference paper, so dubious peer review. N=12.
Mo 2020 No effect No effect. Gray lit. COPD patients.
Person 2018 No effect No effect. 6 minute walking test.
Pifarre 2020 Effect Small effect. Tiny sample (n=8). Questionable control of order of test conditions. Exercise.
Porcari 2016 Effect Irrelevant – like Jagim, concerns an elevation training mask.
Rebmann 2013 Effect No effect. “There were no changes in nurses’ blood pressure, O2 levels, perceived comfort, perceived thermal comfort, or complaints of visual difficulties compared with baseline levels.” Also, no control, as in Beder.
Roberge 2012 No effect No effect. N=20.
Roberge 2014 No effect No effect. N=22. Pregnancy.
Tong 2015 Effect Effect. Exercise during regnancy.

If there’s a pattern here, it’s lots of underpowered small sample studies with design defects. Morover, there are some blatant errors in assessment of relevance (Jagim, Porcari) and inclusion of uncontrolled studies (Beder, Rebmann, maybe Pifarre). In other words, this is 30% rubbish, and the rubbish is all on the “effect” side of the scale.

If the authors did a poor job assessing the studies they included, I also have to wonder whether they did a bad screening job. That turns out to be hard to determine without more time. But a quick search does reveal that there has been an explosion of interest in the topic, with a number of new studies in high-quality journals with better control designs. Regrettably, sample sizes still tend to be small, but the results are generally not kind to the assertions in the health order:

Mapelli et al. 2021:

Conclusions Protection masks are associated with significant but modest worsening of spirometry and cardiorespiratory parameters at rest and peak exercise. The effect is driven by a ventilation reduction due to an increased airflow resistance. However, since exercise ventilatory limitation is far from being reached, their use is safe even during maximal exercise, with a slight reduction in performance.

Chan, Li & Hirsch 2020:

In this small crossover study, wearing a 3-layer nonmedical face mask was not associated with a decline in oxygen saturation in older participants. Limitations included the exclusion of patients who were unable to wear a mask for medical reasons, investigation of 1 type of mask only, Spo2 measurements during minimal physical activity, and a small sample size. These results do not support claims that wearing nonmedical face masks in community settings is unsafe.

Lubrano et al. 2021:

This cohort study among infants and young children in Italy found that the use of facial masks was not associated with significant changes in Sao2 or Petco2, including among children aged 24 months and younger.

Shein et al. 2021:

The risk of pathologic gas exchange impairment with cloth masks and surgical masks is near-zero in the general adult population.

A quick trip to PubMed or Google Scholar provides many more.

Verdict: a sloppy meta-analysis is garbage-in, garbage-out.

Bottom Line

Montana DPHHS has failed to verify its sources, ignores recent literature and therefore relies on far less than the best available science in the construction of its flawed order. Its sloppy work will fan the flames of culture-war conspiracies and endanger the health of Montanans.

Confusing the decision rule with the system

In the NYT:

To avoid quarantining students, a school district tries moving them around every 15 minutes.

Oh no.

To reduce the number of students sent home to quarantine after exposure to the coronavirus, the Billings Public Schools, the largest school district in Montana, came up with an idea that has public health experts shaking their heads: Reshuffling students in the classroom four times an hour.

The strategy is based on the definition of a “close contact” requiring quarantine — being within 6 feet of an infected person for 15 minutes or more. If the students are moved around within that time, the thinking goes, no one will have had “close contact” and be required to stay home if a classmate tests positive.

For this to work, there would have to be a nonlinearity in the dynamics of transmission. For example, if the expected number of infections from 2 students interacting with an infected person for 10 minutes each were less than the number from one student interacting with an infected person for 20 minutes, there might be some benefit. This would be similar to a threshold in a dose-response curve. Unfortunately, there’s no evidence for such an effect – if anything, increasing the number of contacts by fragmentation makes things worse.

Scientific reasoning has little to do with the real motivation:

Greg Upham, the superintendent of the 16,500-student school district, said in an interview that contact tracing had become a huge burden for the district, and administrators were looking for a way to ease the burden when they came up with the movement idea. It was not intended to “game the system,” he said, but rather to encourage the staff to be cognizant of the 15-minute window.

Regardless of the intent, this is absolutely an example of gaming the system. However, you game rules, but you can’t fool mother nature. The 15-minute window is a decision rule for prioritizing contact tracing, invented in the context of normal social mixing. Administrators have confused it with a physical phenomenon. Whether or not they intended to game the system, they’re likely to get what they want: less contact tracing. This makes the policy doubly disastrous: it increases transmission, and it diminishes the preventive effects of contact tracing and quarantine. In short order, that means more infections. A few doublings of cases will quickly overwhelm any reduction in contact tracing burden from shuffling students around.

I think the administrators who came up with this might want to consider adding systems thinking to the curriculum.