Claims by AI chatbots, engineers and Nobel prize winners notwithstanding, absence of correlation does not prove absence of causation, any more than presence of correlation proves presence of causation. Bard outlines several reasons from noise and nonlinearity, but missed a key one: bathtub statistics.
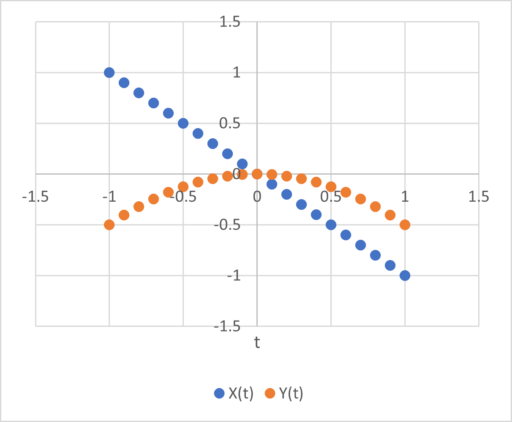
Here’s a really simple example of how this reasoning can go wrong. Consider a system with a stock Y(t) that integrates a flow X(t):
X(t) = -t
Y(t) = ∫X(t)dt
We don’t need to simulate to solve for Y(t) = -1/2*t^2 +C.
Over the interval t=[-1,1] the X and Y time series look like this:
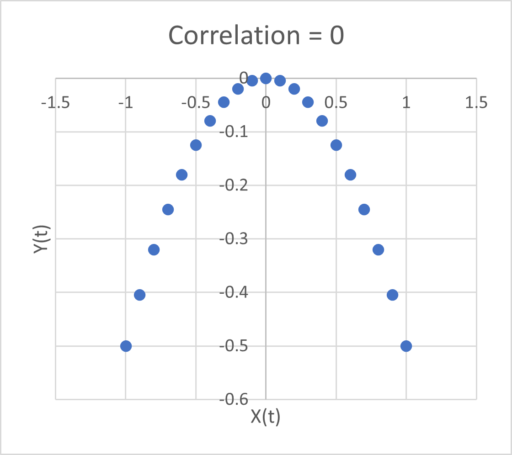
The X-Y relationship is parabolic, with correlation zero:
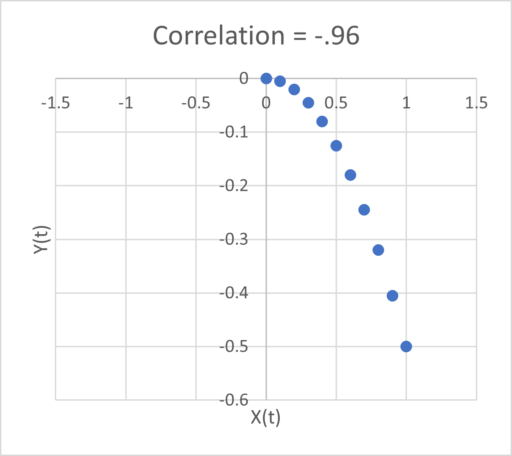
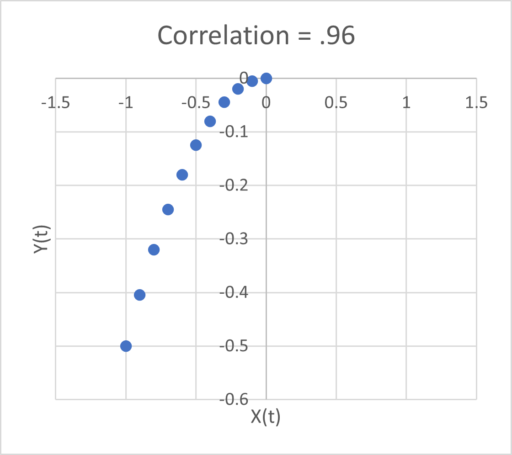
Zero correlation can’t mean “not causal” because we constructed the system to be causal. Even worse, the sign of the relationship depends on the subset of the interval you examine:
This is not the only puzzling case. Consider instead:
X(t) = 1
Y(t) = ∫X(t)dt = t + C
In this case, X(t) has zero variance. But Corr(X,Y) = Cov(X,Y)/σ(X)σ(Y) which is 0/0. What are we to make of that?
This pathology can also arise from feedback. Consider a thermostat that controls a heater that operates in two states (on or off). If the heater is fast, and the thermostat is sensitive with a narrow temperature band, then σ(temperature) will be near 0, even though the heater is cycling with σ(heater state)>0.