November 2019 - MetaSD

Seven Deadly Sins of SD Structure

Obey these simple rules to avoid garbage-in->garbage-out.

There’s a lot of art to modeling, and more generally to managing complex systems. But there’s also some craft to it: simple, mechanical steps that must be followed, almost without exception. Woodworkers know that when you’re using a chisel or plane, you cut with the grain, not across it. Knowing that isn’t sufficient to make a nice-looking chair, but at least your funny-looking chair won’t have ugly tearout.

So what are the rules for classic System Dynamics? Here are a few:

Unbalanced or missing units. It’s possible to build a correct model without units, but most people (including me) are unlikely to manage it. Even if the model is right in some sense, without units it’s still unintelligible to others.
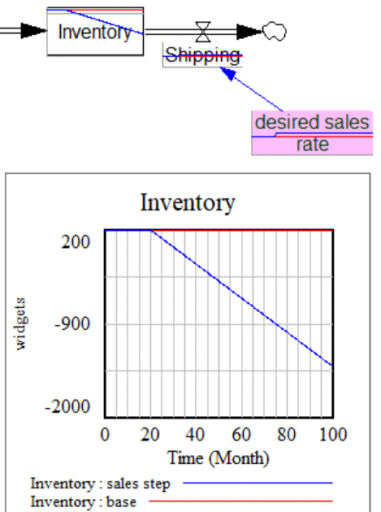
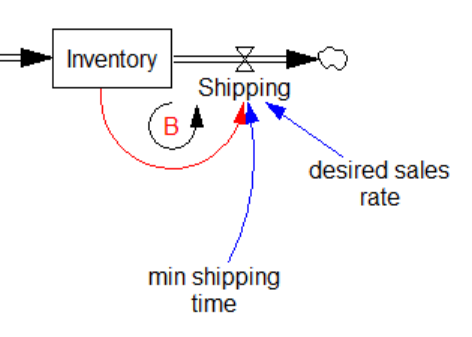
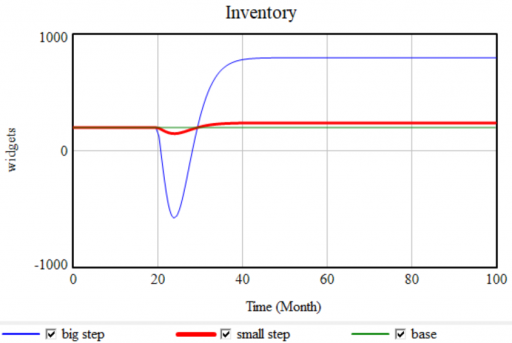
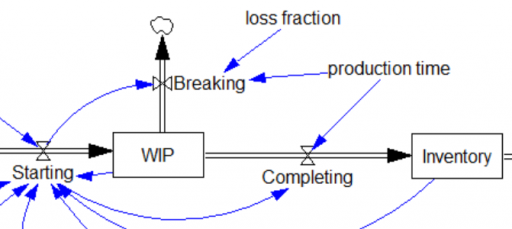
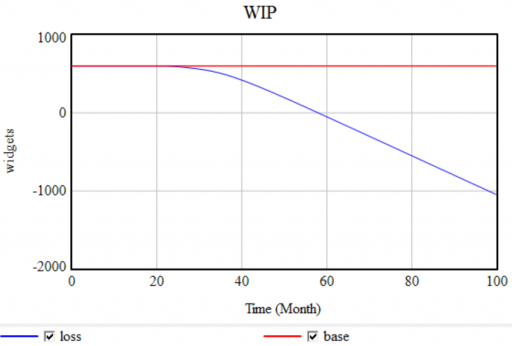
No FONFOO. Every physical stock needs First-Order Negative Feedback On the Outflows. This means the equations ensure that the outflow goes to 0 as the stock goes to 0 – not after a while, but now and forever. This ensures conservation of stuff: no inventory -> no sales. Nonphysical stocks often require this treatment as well, unless negative values are permitted by definition.
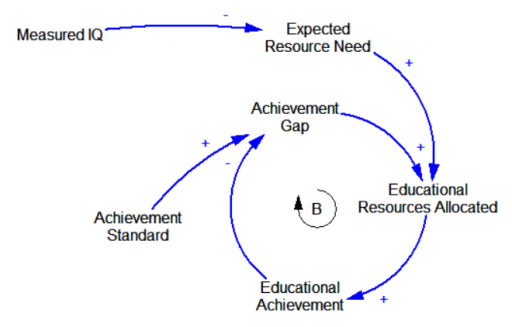
Embedded parameters. A colleague just found an equation in a spreadsheet model reading something like =A2*EXP(-C4/C1) + 4. The “4” was just an arbitrary fudge factor on the answer. This should never happen; anything more complex than the 1 in 1/x should always be exposed as a distinct, named variable with appropriate units.
- Corollary: the embedded parameter often represents an implicit goal. For example, in inventory adjustment = (1000-inventory)/inventory adj time, the goal of 1000 units should be made explicit.
Discrete time. Generally, your model should be independent of the TIME STEP and simulation method. Decision rules should integrate information smoothly, not at arbitrary point lags.
Discrete logic. Sometimes I see equations that involve big cascades of logical statements: IF THEN ELSE( inventory < 100 :AND: price > 2, do x, IF THEN ELSE( inventory > 200 :AND: expected sales > inventory/desired coverage, do y, IF THEN ELSE( … Constructions like this are hard to read and hard to debug, and they often fail important reality checks. They might be appropriate in tactical cases where reality has discernible, discrete rules. But they’re seldom helpful in strategic models involving the aggregate behavior of many agents or objects.
Overuse of delays. Every feedback loop must include a stock. This is a consequence of “time is what keeps everything from happening at once.” If there’s no integration in a loop, then feedback would run infinitely fast. Sometimes, confronted with an apparently simultaneous loop, modelers just insert a SMOOTHI or similar function that contains a stock. This may not be good enough; the stock in the loop can’t be arbitrary; it has to have real meaning.
- It’s also possible to commit the opposite sin: underuse of delays. Perceptions lag reality, and people often underestimate the extent to which this is true. Decision rules in your model should reflect this, but I think it’s more a matter of art than craft.
Taking the cream out of the coffee. Suppose you have a stock of people, with a coflow of money used to keep track of the average wealth of people in the stock. It’s then tempting to handle a thought experiment like, “ok, what if all the rich people leave the country?” by siphoning off a greater-than-average share of the money alongside each departing person. This violates the assumption that a stock is the complete representation of system state. What if, for example, the rich people already left, so that the remainder are uniformly poor? If the distinction is important, you simply must disaggregate the people into classes.

Like all rules, these are made to be broken, but exceptions are rare, and require that you really know what you’re doing. They are important because they ensure compliance with Reality Checks that should remain inviolate for strong reasons. If your population model isn’t conserving people, you have a problem.

Incidentally, at least half of these are mentioned in Appendix O of Industrial Dynamics, “Beginners’ Difficulties.” However, these are not just tricks for beginners: everyone can benefit from keeping them in mind, just as professional pilots rely on checklists.

I’m eager to hear your thoughts in the comments. What rules did I miss?

The importance of FONFOO

Every physical stock needs First Order Negative Feedback On Outflows.

I’ve been approached several times recently with questions about stocks behaving badly. All involved a construction something like the following:

This is a simple inventory control system, in which I’ve short-circuited the production start feedback by making Starting exogenous and equal to the desired sales rate. Therefore, there are really only two interesting equations:

Shipping=desired sales rate
Units: widgets/Month

Completing=DELAY3( Starting, production time )
Units: widgets/Month

Notice that there’s a violation of standard practice here, in that there’s a flow-to-flow connection from Starting to Completing. This is due to the DELAY3 function, which is shorthand for an explicit 3rd-order delay:

The 3rd-order delay is often a realistic compromise between a 1st-order system, in which the first completions arrive too quickly after Starting, and a pipeline delay or conveyor, which has too little dispersion to represent an aggregation of many items. (See the Delay Sandbox and Erlang models for examples.)

So, how can we break this model?

I always like to start with some tests in Synthesim. A good one is to stress the system with a step in the desired sales rate, here from 100 to 120. You can immediately spot a problem:

Inventory goes negative, because Shipping proceeds, even when inventory is exhausted. That can’t happen in reality, but it happens here because Shipping is not a function of Inventory. There’s a simple fix:

Shipping=MIN(desired sales rate, Inventory/min shipping time)
Units: widgets/Month

Above, min shipping time is a time constant representing the minimum time needed to deplete inventory. It’s common to set min shipping time = TIME STEP in situations where you want to prevent negative inventory, and the precise dynamics of inventory exhaustion are not central to the model. (If it matters, see Dynamics of the Last Twinkie.)

This is FONFOO. The “first order negative feedback” refers to the balancing loop created by the Inventory/min shipping time term in the fixed equation:

The tricky thing about this situation is that if Starting had been endogenous, the negative inventory problem would have been much harder to spot. Here’s the same model with a simple decision rule for Starting that maintains Inventory and WIP and desired levels:

Now, a modest step in sales doesn’t cause negative inventory, as long as the production process can replenish it in time. It takes a huge step (from 100 to 400 widgets/month) to reveal the problem:

This means that experiments on a model as a whole may not reveal problems that lurk in the details of the model, unless they’re quite extreme. I recommend extreme tests, but prevention is more important. Simply make it a habit to implement FONFOO everywhere, and you won’t have problems. (Note that we could automate this in Vensim, but we don’t, because doing so can easily mask other formulation problems, fall short of the control that’s really needed, or impede situations in which nonphysical stocks are intentionally negative.)

Now let’s take a look at the 3rd-order production delay surrounding WIP. As presented above, it works fine – it’s mathematically equivalent to the explicit 3rd-order aging chain. However, there are consistency issues to be aware of. Consider the following augmentation of the structure, representing stock losses (the flow of Breaking) from WIP:

Completing=DELAY3( Starting, production time )
Units: widgets/Month
Breaking=DELAY3(Starting*loss fraction,production time)
Units: widgets/Month

Completing is still a delayed function of Starting. But Completing is not directly aware of WIP and therefore unaware of the consequences of Breaking. This is a violation of FONFOO because the DELAY3 function contains internal states that are independent of the WIP stock. Consider what happens if the loss fraction is nonzero. In equilibrium, the output of DELAY3 is equal to the inflow. So, the outflow from WIP would be Breaking+Completing, which equals Starting+Starting*loss fraction, which is of course greater than starting for any nonzero loss.

A step in the loss function from 0 to 0.2 causes WIP to go negative:

Again, the remedy is simple. In most cases, you can keep the DELAY function if you ensure that the inflows and outflows are conserved. For example, adding a term:

Completing=DELAY3( Starting*(1-loss fraction), production time )
 Units: widgets/Month
 Breaking=DELAY3(Starting*loss fraction,production time)
 Units: widgets/Month

In some situations, it may be desirable to switch to an explicit aging chain in order to handle an idiosyncratic distribution of losses across the WIP process, or other complexities. Often arrays are useful for such purposes.

You may encounter the DELAY1 function in similar circumstances. DELAY1 is just like DELAY3, except that it’s first order. So, the system:

inflow = 10 ~ widgets/month
stock = INTEG(inflow-outflow, inflow*tau) ~ widgets
outflow = stock/tau ~ widgets/month
tau = 6 ~ months

is identical to the system:

inflow = 10 ~ widgets/month
stock = INTEG(inflow-outflow, inflow*tau) ~ widgets
outflow = DELAY1(inflow,tau) ~ widgets/month
tau = 6 ~ months

In this case, there’s really no reason to use the DELAY1 – it just obfuscates the first-order stock dynamics. However, there’s still a potential pitfall, which also applies to DELAY3. The initialization is important. The DELAY functions generally initialize their internal stocks in equilibrium, as if the inflow had been at its initial level historically. Therefore the stock above needs to be initialized the same way, to inflow*tau. If you want to use some other value, like zero, you need to use DELAY3i (or its equivalent) to set the stock and delay function to a consistent set of assumptions.

In reviewing other models, you may also find hybrid approaches, like:

inflow = 10 ~ widgets/month
stock = INTEG(inflow-outflow, inflow*tau) ~ widgets
outflow = DELAY1(stock/tau,tau) ~ widgets/month
tau = 6 ~ months

This is another FONFOO violation. The outflow is indeed a function of the stock, which ensures that the outflow eventually goes to zero when the stock is exhausted. But this does not create a 1st-order negative feedback loop; the DELAY1 contains an additional stock. So, this is SONFOO (second order negative feedback on the outflow), which might be useful for creating an oscillator, but won’t solve your supply chain problems.

If you make FONFOO a habit, you’ll have one less thing to worry about when you start exploring the interesting, complex behaviors of your models.

Eugenics rebooted – what could go wrong?

Does DNA IQ testing create a meritocracy, or merely reinforce existing biases?

Technology Review covers new efforts to use associations between DNA and IQ.

… Intelligence is highly heritable and predicts important educational, occupational and health outcomes better than any other trait. Recent genome-wide association studies have successfully identified inherited genome sequence differences that account for 20% of the 50% heritability of intelligence. These findings open new avenues for research into the causes and consequences of intelligence using genome-wide polygenic scores that aggregate the effects of thousands of genetic variants.

The new genetics of intelligence

Robert Plomin and Sophie von Stumm

I have no doubt that there’s much to be learned here. However, research is not all they’re proposing:

IQ GPSs will be used to predict individuals’ genetic propensity to learn, reason and solve problems, not only in research but also in society, as direct-to-consumer genomic services provide GPS information that goes beyond single-gene and ancestry information. We predict that IQ GPSs will become routinely available from direct-to-consumer companies along with hundreds of other medical and psychological GPSs that can be extracted from genome-wide genotyping on SNP chips. The use of GPSs to predict individuals’ genetic propensities requires clear warnings about the probabilistic nature of these predictions and the limitations of their effect sizes (BOX 7).

Although simple curiosity will drive consumers’ interests, GPSs for intelligence are more than idle fortune telling. Because intelligence is one of the best predictors of educational and occupational outcomes, IQ GPSs will be used for prediction from early in life before intelligence or educational achievement can be assessed. In the school years, IQ GPSs could be used to assess discrepancies between GPSs and educational achievement (that is, GPS-based overachievement and underachievement). The reliability, stability and lack of bias of GPSs make them ideal for prediction, which is essential for the prevention of problems before they occur. A ‘precision education’ based on GPSs could be used to customize education, analogous to ‘precision medicine’

There are two ways “precision education” might be implemented. An egalitarian model would use information from DNA IQ measurements to customize resource allocations, so that all students could perform up to some common standard:

An efficiency model, by contrast, would use IQ measurements to set achievement expectations for each student, and customize resources to ensure that students who are underperforming relative to their DNA get a boost:

This latter approach is essentially a form of tracking, in which DNA is used to get an early read on who’s destined to flip bonds, and who’s destined to flip burgers.

One problem with this scheme is noise (as the authors note, seemingly contradicting their own abstract’s claim of reliability and stability). Consider the effect of a student receiving a spuriously low DNA IQ score. Under the egalitarian scheme, they receive more educational resources (enabling them to overperform), while under the efficiency scheme, resources would be lowered, leading self-fulfillment of the predicted low performance. The authors seem to regard this as benign and self-correcting:

By contrast, GPSs are ‘less dangerous’ because they are intrinsically probabilistic, not hardwired and deterministic like single-gene disorders. It is important to recall here that although all complex traits are heritable, none is 100% heritable. A similar logic can be applied to IQ scores: although they have great predictive validity for key life outcomes, IQ is not deterministic but probabilistic. In short, an individual is always more than the sum of their genes or their IQ scores.

I think this might be true when you consider the local effects on the negative loops governing resource allocation. But I don’t think that remains true when you put it in context. Education is a nest of positive feedbacks. This creates path dependence that amplifies errors in resource allocation, whether they come from subjective teacher impressions or DNA measurements.

In a perfect world, DNA-IQ provides an independent measurement that’s free of those positive feedbacks. In that sense, it’s perfectly meritocratic:

But how do you decide what to measure? Are the measurements good, or just another way to institutionalize bias? This is hotly contested. Let’s suppose that problems of gender and race/ethnicity bias have been, or can be solved. There are still questions about what measurements correlate with better individual or societal outcomes. At some point, implicit or explicit choices have to be made, and these are not value-free. They create reinforcing feedbacks:

I think it’s inevitable that, like any other instrument, DNA IQ scores are going to reflect the interests of dominant groups in society. (At a minimum, I’d be willing to bet that IQ tests don’t measure things that would result in low scores for IQ test designers.) If that means more Einsteins, Bachs and Ghandis, maybe it’s OK. But I don’t think that’s guaranteed to lead to a good outcome. First, there’s no guarantee that a society composed of apparently high-performing individuals is in itself high-performing. Second, the dominant group may be dominant, not by virtue of faster CPUs in their heads, but something less appetizing.

I think there’s no guarantee that DNA IQ will not reflect attributes that are dysfunctional for society. We would hate to inadvertently produce more Stalins and Mengeles by virtue of inadvertent correlations with high achievement of less virtuous origin. And certainly, like any instrument used for high-stakes decisions, the pressure to distort and manipulate results will increase with use.

Note that if education is really egalitarian, the link between Measured IQ and Educational Resources Allocated reverses polarity, becoming negative. Then the positive loops become negative loops, and a lot of these problems go away. But that’s not often a choice societies make, presumably because egalitarian education is in itself contrary to the interests of dominant groups.

I understand researchers’ optimism for this technology in the long run. But for now, I remain wary, due to the decided lack of systems thinking about the possible side effects. In similar circumstances, society has made poor choices about teacher value added modeling, easily negating any benefits it might have had. I’m expecting a similar outcome here.