Most System Dynamics software includes a pair of TREND and FORECAST functions. For historic reasons, these are typically the simplest possible first-order structure, which is fine for continuous, deterministic models, but not the best for applications with noise or real data. The waters are further muddied by the fact that Excel has a TREND function that’s really FORECASTing, plus newer FORECAST functions with methods that may differ from typical SD practice. Business Dynamics describes a third-order TREND function that’s considerably better for real-world applications.
As a result of all this variety, I think trend measurement and forecasting remain unnecessarily mysterious, so I built the model below to compare several approaches.
Goal
The point of TREND and FORECAST functions is to model the formation of expectations in a way that closely matches what people in the model are really doing.
This could mean a wide variety of things. In many cases, people aren’t devoting formal thought to observing and predicting the phenomenon of interest. In that case, adaptive expectations may be a good model. The implementation in SD is the SMOOTH function. Using a SMOOTH to set expectations says that people expect the future to be like the past, and they perceive changes in conditions only gradually. This is great if the forecasted variable is in fact stationary, or at least if changes are slow compared to the perception time. On the other hand, for a fast-evolving situation like COVID19, delay can be fatal – literally.
For anything that is in fact changing (or that people perceive to be changing), it makes sense to project changes into the future with some kind of model. For a tiny fraction of reality, that might mean a sophisticated model: multiple regression, machine learning, or some kind of calibrated causal model, for example. However, most things are not subject to that kind of sophisticated scrutiny. Instead, expectations are likely to be formed by some kind of simple extrapolation of past trends into the future.
In some cases, things that are seemingly modeled in a sophisticated way may wind up looking a lot like extrapolation, due to human nature. The forecasters form a priori expectations of what “good” model projections look like, based on fairly naive adaptive-extrapolative expectations and social processes, and use those expectations to filter the results that are deemed acceptable. This makes the sophisticated results look a lot like extrapolation. However, the better the model, the harder it is for this to happen.
The goal, by the way, is generally not to use trend-like functions to make a forecast. Extrapolation may be perfectly reasonable in some cases, particularly where you don’t care too much about the outcome. But generally, you’re better off with a more sophisticated model – the whole point of SD and other methods is to address the feedback and nonlinearities that make extrapolation and other simpleminded methods go wrong. On the other hand, simple extrapolation may be great for creating a naive or null forecast to use as a benchmark for comparison with better approaches.
Basics
So, let’s suppose you want to model the expectations for something that people perceive to be (potentially) steadily increasing or decreasing. You can visit St. Louis FRED and find lots of economic series like this – GDP, prices, etc. Here’s the spot price of West Texas Intermediate crude oil:
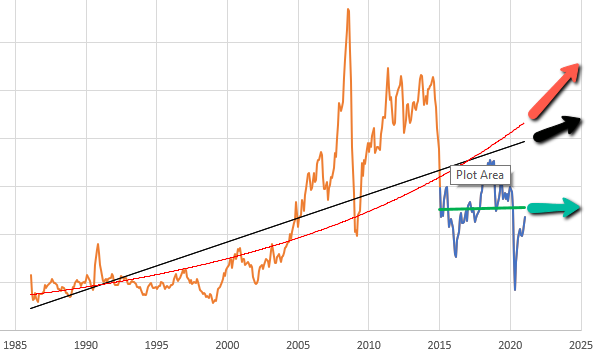
Given this data, there are immediately lots of choices. Thinking about someone today making an investment conditional on future oil prices, should they extrapolate linearly (black and green lines) or exponentially (red line)? Should they use the whole series (black and red) or just the last few years (green)? Each of these implies a different forecast for the future.
Suppose we have some ideas about the forecast horizon, desired sensitivity to noise, etc. How do we actually establish a trend? One option is linear regression, which is just a formal way of eyeballing a straight line that fits some data. It works well, but has some drawbacks. First, it assigns equal weight to all the data throughout the interval, and zero weight to anything outside the interval. That may be a poor model for perceptual processes, where the most recent data has the greatest salience to the decision maker. Second, it’s computation- and storage-intensive: you have to do a lot of math, and keep track of every data point within the window of interest. That’s fine if it resides in a spreadsheet, but not if it resides in someone’s head.
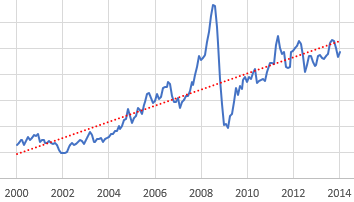
The trend-like functions make an elegant simplification that addresses the drawbacks of regression. It’s based on the following observation:*
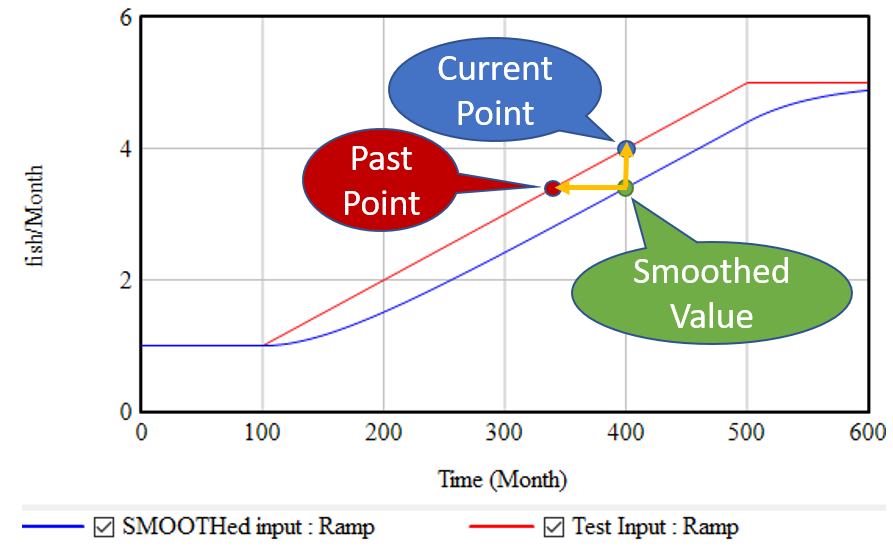
If, as above, you take a growing input (red line) and smooth it exponentially (using the SMOOTH function, or an equivalent first order goal-gap structure), you get the blue line: another ramp, that lags the input with a delay equal to the smoothing time. This means that, at month 400, we know two points: the current value of the input, and the current value of the smoothed input. But the smoothed value represents the past value of the input, in this case 60 months previous. So, we can use these two points to determine the slope of the red line:
(1) slope = (current - smoothed) / smoothing time
This is the slope in terms of input units per time. It’s often convenient to compute the fractional slope instead, expressing the growth as a fractional increase in the input per unit time:
(2) fractional slope = (current - smoothed) / smoothed / smoothing time
This is what the simple TREND functions in SD software typically report. Note that it blows up if the smoothed quantity reaches 0, while the linear method (1) does not.
If we think the growth is exponential, rather than a linear ramp, we can compute the growth rate in continuous time:
(3) fractional growth rate = LN( current / smoothed ) / smoothing time
This has pros and cons. Obviously, if a quantity is really growing exponentially, it should be measured that way. But if we’re modeling how people actually think, they may extrapolate linearly when the underlying behavior is exponential, thereby greatly underestimating future growth. Note that the very idea of forecasting exponentially assumes that the values involved are positive.
Once you know the slope of the (estimated) line, you can extrapolate it into the future via a method that corresponds with the measurement:
(1b) future value = current + slope * forecast horizon (2b) future value = current * (1 + fractional slope * forecast horizon) (3b) future value = current * EXP( fractional growth rate * forecast horizon )
Typical FORECAST functions use (2b).
*There’s a nice discussion of this in Appendix L of Industrial Dynamics, around figure L-3.
Refinements
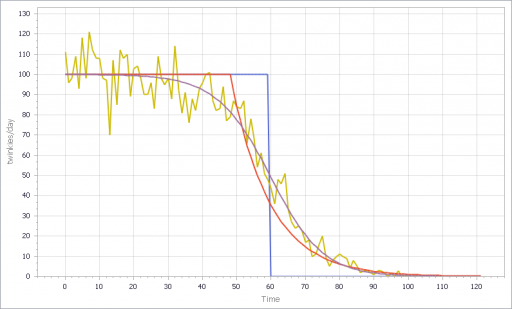
The strategy above has the virtue of great simplicity: you only need to keep track of one extra stock, and the computation needed to extrapolate is minimal. It works great for continuous models. Unfortunately, it’s not very resistant to noise and discontinuities. Consider what happens if the input is not a smooth line, but a set of noisy points scattered around the line:
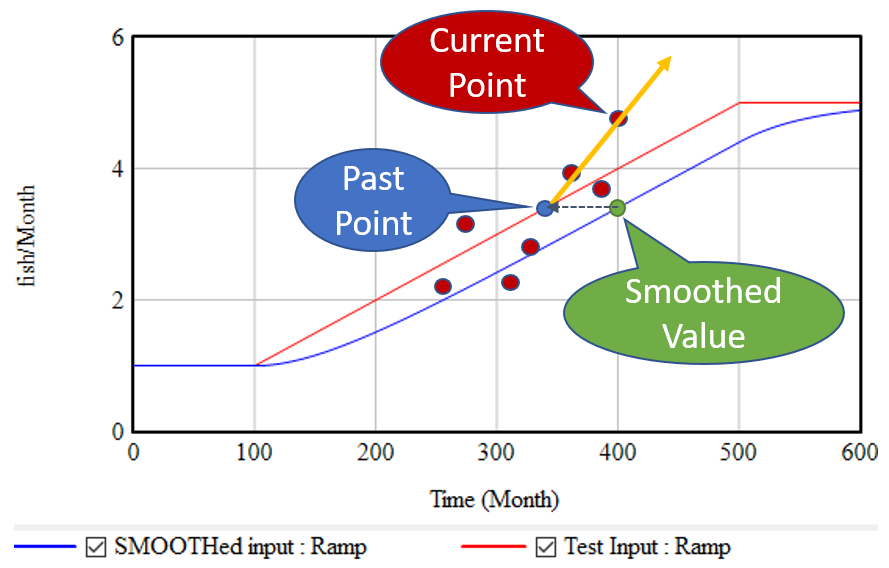
The SMOOTH function filters the data, so the past point (blue) may still be pretty close to the underlying input trend (red line). However, the extrapolation (orange line) relies only on the past point and the single current point. Any noise or discontinuity in the current point therefore can dramatically influence the slope estimate and future projections. This is not good.
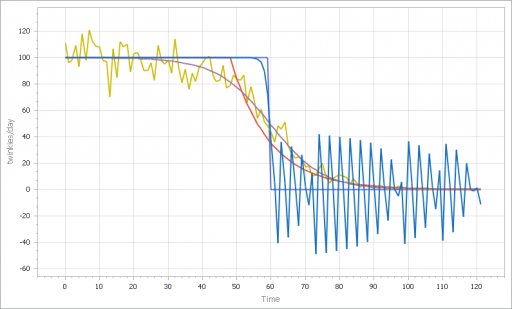
Similar perverse behaviors happen if the input is a pulse or step function. For example:
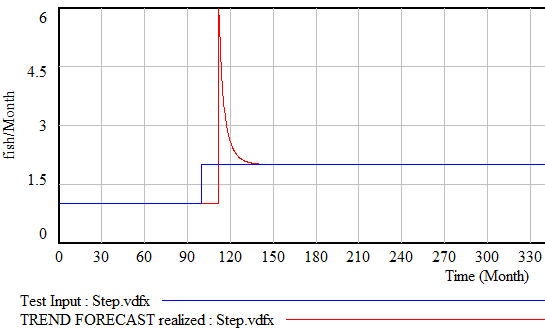
Fortunately, simple functions can be saved. In Expectation Formation in Behavioral Simulation Models, John Sterman describes an alternative third-order TREND function that improves robustness and realism. The same structure can be found in the excellent discussion of expectations in Business Dynamics, Chapter 16.
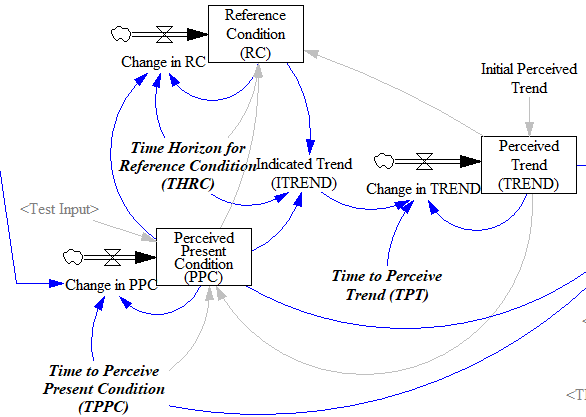
I’ll leave the details to the article, but the basic procedure is:
- Recognize that the input is not perceived instantaneously, but only after some delay (represented by smoothing). This might capture the fact that formal accounting procedures only report results with a lag, or that you only see the price of cheese at the supermarket intermittently.
- Track a historic point (the Reference Condition), by smoothing, as in the simpler methods.
- Measure the Indicated Trend as the fractional slope between the Perceived Present Condition and the Reference Condition.
- Smooth the Indicated Trend again to form the final Perceived Trend. The smoothing prevents abrupt changes in the indicated trend from causing dramatic overshoots or undershoots in the trend estimate and extrapolations that use it.
There’s an intermediate case that’s actually what I’m most likely to reach for when I need something like this: second-order smoothing. There are actually several very similar approaches (see double exponential smoothing for example) in the statistical literature. You have to be a little cautious, because these are often expressed in discrete time and therefore require a little thought to adapt to continuous time and/or unequal data intervals.
The version I use does the following:
(4) smoothed input = SMOOTH( input, smoothing time ) (5) linear trend = (input-smoothed input) / smoothing time (6) smoothed trend = SMOOTH( linear trend, trend smoothing time ) (7) forecast = smoothed input + smoothed trend*(smoothing time + forecast horizon)
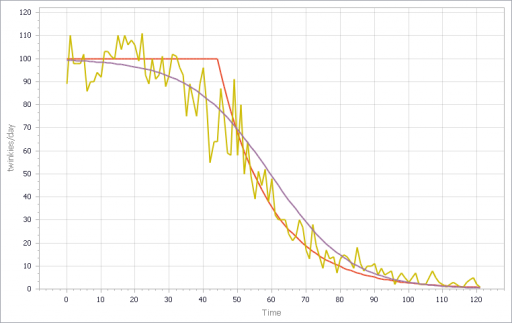
This provides most of what you want in a simple extrapolation method. It largely ignores a PULSE disturbance. Overshoot is mild when presented with a STEP input (as long as the smoothing times are long enough). It largely rejects noise, but still tracks a real RAMP accurately.
Back to regression
SD models typically avoid linear regression, for a reasons that are partly legitimate (as mentioned above). But it’s also partly cultural, as a reaction to incredibly stupid regressions that passed for models in other fields around the time of SD’s inception. We shouldn’t throw the baby out with that bathwater.
Fortunately, while most software doesn’t make linear regression particularly accessible, it turns out to be easy to implement an online regression algorithm with stocks and flows with no storage of data vectors required. The basic insight is that the regression slope (typically denoted beta) is given by:
(8) slope = covar(x,y) / var(x)
where x is time and y is the input to be forecasted. But var() and covar() are just sums of squares and cross products. If we’re OK with having exponential weighting of the regression, favoring more recent data, we can track these as moving sums (analogous to SMOOTHs). As a further simplification, as long as the smoothing window is not changing, we can compute var(x) directly from the smoothing window, so we only need to track the mean and covariance, yielding another second-order smoothing approach.
If the real decision makers inspiring your model are actually using linear regression, this may be a useful way to implement it. The implementation can be extended to equal weighting over a finite interval if needed. I find the second-order smoothing approach more intuitive, and it performs just as well, so I tend to prefer that in most cases.
Extensions
Most of what I’ve described above is linear, i.e. it assumes linear growth or decline of the quantity of interest. For a lot of things, exponential growth will be a better representation. Equations (3) and (3b) assume that, but any of the other methods can be adapted to assume exponential behavior by operating on the logarithm of the input, and then inverting that with exp(…) to form the final output.
All the models described here share one weakness: cyclical inputs.
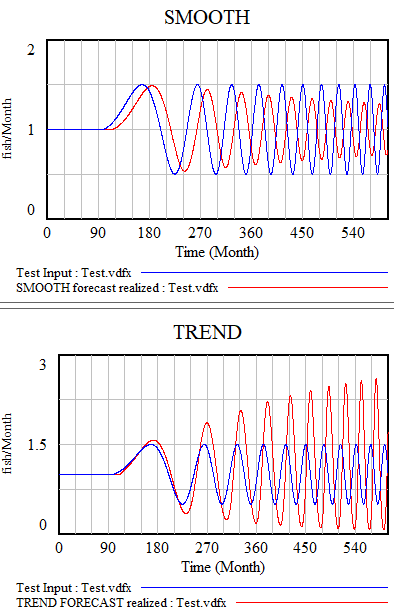
When presented with a sin wave, the simplest approach – smoothing – just bulldozes through. The higher the frequency, the less of the signal passes into the forecast. The TREND function can follow a wave if the period is longer than the smoothing time. If the dynamics are faster, it starts to miss the turning points and overshoot dramatically. The higher-order methods are better, but still not really satisfactory. The bottom line is that your projection method must use a model capable of representing the signal, and none of the methods above embodies anything about cyclical behavior.
There are lots of statistical approaches to detection of seasonality, which you can google. Many involve binning techniques, similar to those described in Appendix N of Industrial Dynamics, Self Generated Seasonal Cycles.
The model
The Vensim model, with changes (.cin) files implementing some different experiments:
I developed this in DSS and forgot to test PLE before uploading. If you have issues, please comment and I’ll adapt it to work.
A Ventity version is on the way.