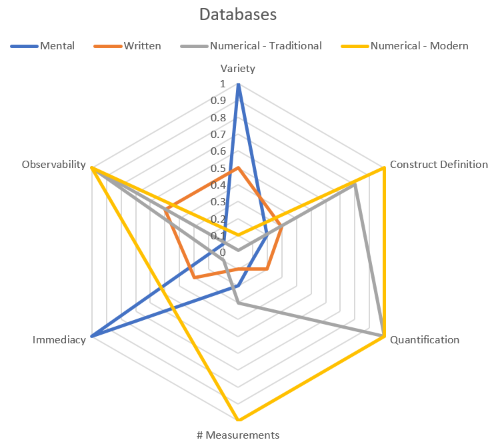
I like Jay Forrester’s “Next 50 Years” reflection, except for his perspective on data:
I believe that fitting curves to past system data can be misleading.
OK, I’ll grant that fitting “curves” – as in simple regressions – may be a waste of time, but that’s a bit of a strawdog. The interesting questions are about fitting good dynamic models that pass all the usual structural tests as well as fitting data.
Also, the mere act of fitting a simple model doesn’t mislead; the mistake is believing the model. Simple fits can be extremely useful for exploratory analysis, even if you later discard the theories they imply.
Having a model give results that fit past data curves may impress a client.
True, though perhaps this is not the client you’d hope to have.
However, given a model with enough parameters to manipulate, one can cause any model to trace a set of past data curves.
This is Von Neumann’s elephant. He’s right, but I roll my eyes every time I hear this repeated – it’s a true but useless statement, like all models are wrong. Nonlinear dynamic models that pass SD quality checks usually don’t have anywhere near the degrees of freedom needed to reproduce arbitrary behaviors.
Doing so does not give greater assurance that the model contains the structure that is causing behavior in the real system.
On the other hand, if the model can’t fit the data, why would you think it does contain the structure that is causing the behavior in the real system?
Furthermore, the particular curves of past history are only a special case. The historical curves show how the system responded to one particular combination of random events impinging on the system. If the real system could be rerun, but with a different random environment, the data curves would be different even though the system under study and its essential dynamic character are the same.
This is certainly true. However, the problem is that the particular curve of history is the only one we have access to. Every other description of behavior we might use to test the model is intuitively stylized – and we all know how reliable intuition in complex systems can be, right?
Exactly matching a historical time series is a weak indicator of model usefulness.
Definitely.
One must be alert to the possibility that adjusting model parameters to force a fit to history may push those parameters outside of plausible values as judged by other available information.
This problem is easily managed by assigning strong priors to known parameters in the model calibration process.
Historical data is valuable in showing the characteristic behavior of the real system and a modeler should aspire to have a model that shows the same kind of behavior. For example, business cycle studies reveal a large amount of information about the average lead and lag relationships among variables. A business-cycle model should show similar average relative timing. We should not want the model to exactly recreate a sample of history but rather that it exhibit the kinds of behavior being experienced in the real system.
As above, how do we know what kinds of behavior are being experienced, if we only have access to one particular history? I think this comment implies the existence of intuitive data from other exemplars of the same system. If that’s true, perhaps we should codify those as reference modes and treat them like data.
Again, yielding to what the client wants may be the easy road, but it will undermine the powerful contributions that system dynamics can make.
This is true in so many ways. The client often wants too much detail, or too many scenarios, or too many exogenous influences. Any of these can obstruct learning, or break the budget.
These pages are full of data-free conceptual models that I think are valuable. But I also love data, so I have a different bottom line:
- Data and calibration by themselves can’t make the model worse – you’re adding additional information to the testing process, which is good.
- However, time devoted to data and calibration has an opportunity cost, which can be very high. So, you have to weigh time spent on the data against time spent on communication, theory development, robustness testing, scenario exploration, sensitivity analysis, etc.
- That time spent on data is not all wasted, because it’s a good excuse to talk to people about the system, may reveal features that no one suspected, and can contribute to storytelling about the solution later.
- Data is also a useful complement to talking to people about the system. Managers say they’re doing X. Are they really doing Y? Such cases may be revealed by structural problems, but calibration gives you a sharper lens for detecting them.
- If the model doesn’t fit the data, it might be the data that is wrong or misinterpreted, and this may be an important insight about a measurement system that’s driving the system in the wrong direction.
- If you can’t reproduce history, you have some explaining to do. You may be able to convince yourself that the model behavior replicates the essence of the problem, superimposed on some useless noise that you’d rather not reproduce. Can you convince others of this?
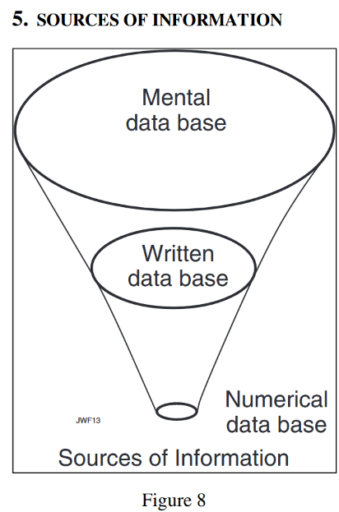 I think the diagram, or at least the concept, is much older than that.
I think the diagram, or at least the concept, is much older than that.