As promised, here’s my solution to the escalator problem … several, actually.
Before getting into the models, a point about simulation vs. analytic solutions. You can solve this problem on pencil and paper with simple algebra. This has some advantages. First, you can be completely data free, by using symbols exclusively. You don’t need to know the height of the stair or a person’s climbing speed, because you can call these Hs and Vc and solve the problem for all possible values. A simulation, by contrast, needs at least notional values for these things. Second, you may be able to draw general conclusions about the solution from its structure. For example, if it takes the form t = H/V, you know there’s some kind of singularity at V=0. With a simulation, if you don’t think to test V=0, you might miss an important special case. It’s easy to miss these special cases in a parameter space with many dimensions.
On the other hand, if there are many dimensions, this may imply that the problem will be difficult or impossible to solve analytically, so simulation may be the only fallback. A simulation also makes it easier to play with the model interactively (e.g., Vensim’s Synthesim mode) and to incorporate features like model-data comparisons and optimization. The ability to play invites experimentation with parameter values you might not otherwise think of. Also, drawing a stock-flow diagram may allow you to access other forms of visual thinking, or analogies with structurally similar systems in different domains.
With that prelude, here’s how I conceived of the problem:
- You’re in a building, at height=0 (feet in my model, but the particular unit doesn’t matter as long as you have and check units).
- Stairs rise to height=100.
- There’s an escalator from 100 to 200 ft.
- Then stairs resume, to infinite height.
- The escalator ascends at 1ft/sec and the climber at 1ft/sec whether on stairs or not.
- At some point, the climber rests for 60sec, at which point their rate of climb is 0, but they continue to ascend if on the escalator.
Of course all the numbers can be changed on the fly, but these concepts at least have to exist.
I think of this as a problem of pure accumulation, with height as a stock. But it turned out that I still needed some feedback to determine where the climber was – on the stairs, or on the escalator:
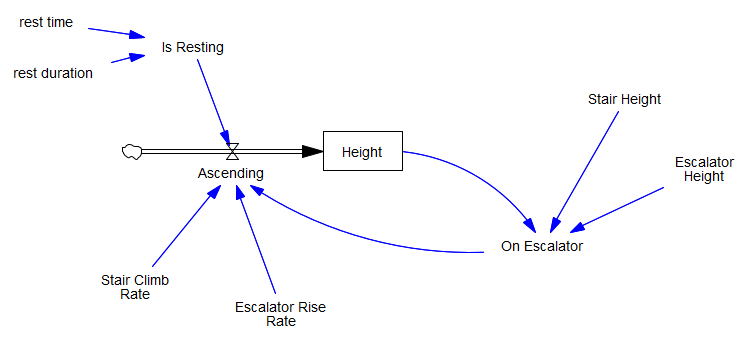
At first it struck me that this was “fake” feedback – an accounting artifact – and that it might go away with an alternate conception. Here’s my implementation of Pradeesh Kumar’s idea, from the SDS Discussion Group on Facebook, with the height to be climbed on the stairs and escalator as a stock, with an outflow as climbing is accomplished: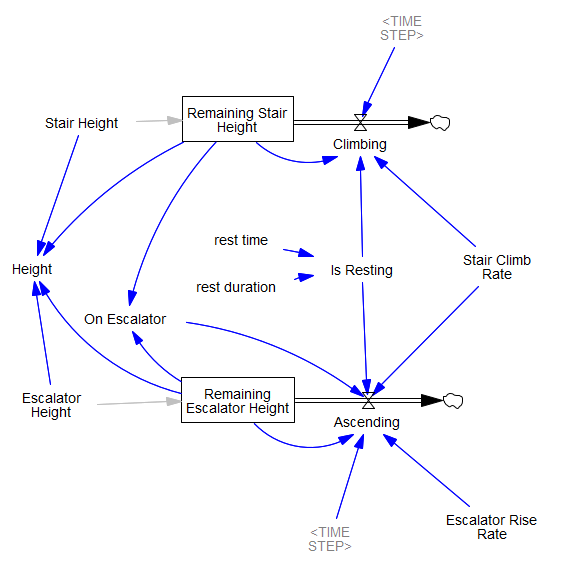 The logical loop is still there, and the rest of the accounting is more complex, so I think it’s inevitable.
The logical loop is still there, and the rest of the accounting is more complex, so I think it’s inevitable.
Finally, I built the same model in Ventity, so I could use multiple entities to quickly store and replicate several scenarios:
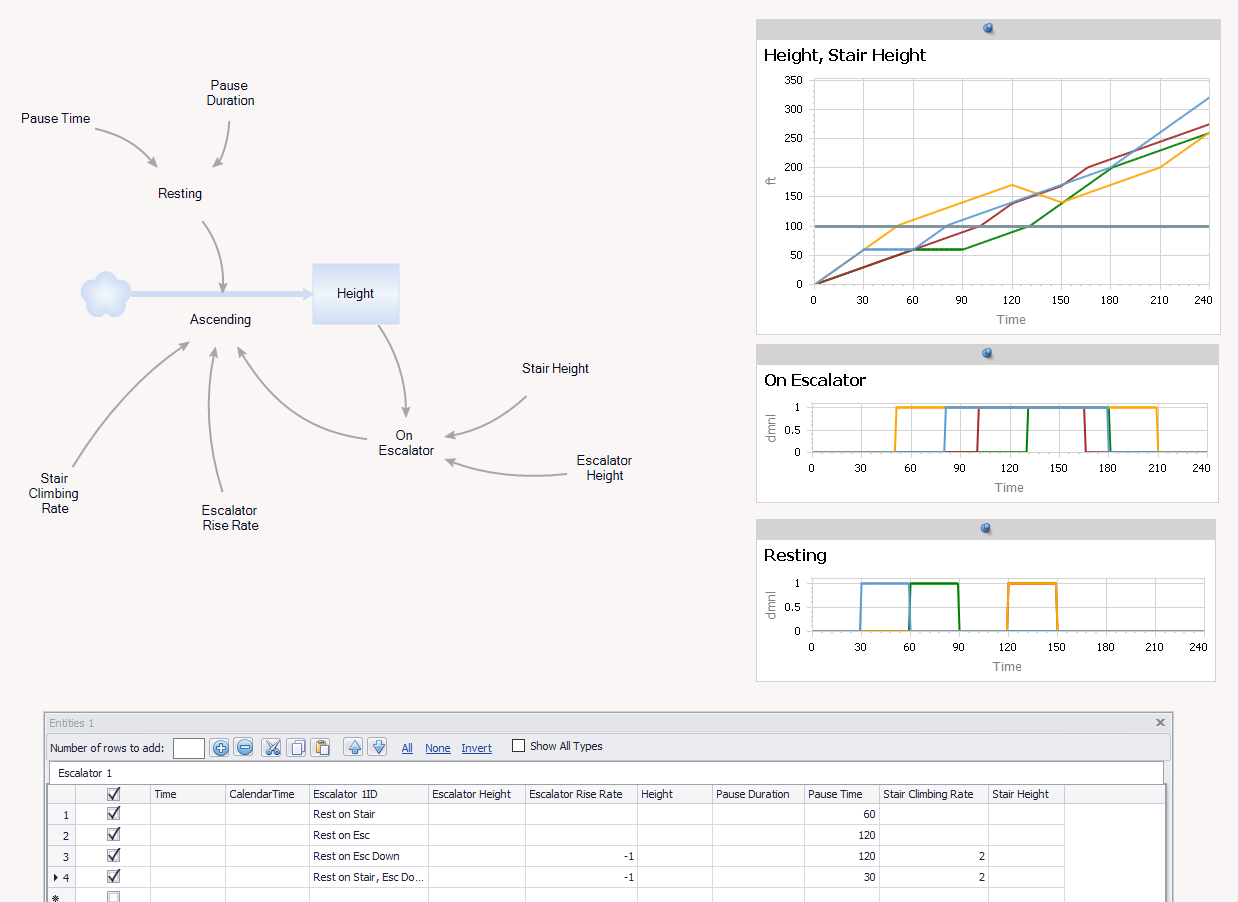
Looking at the Ventity output, resting on the escalator is preferable:
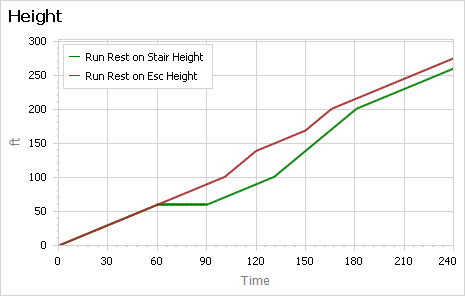
While resting on the stairs, nothing happens. While resting on the escalator, you continue to make gains.
There’s an unstated assumption present in all the twitter answers I’ve seen: the escalator is the up escalator. I actually prefer to go up the down escalator, though it attracts weird looks. If you do that, resting on the escalator is catastrophic, because you lose ground that you previously gained:
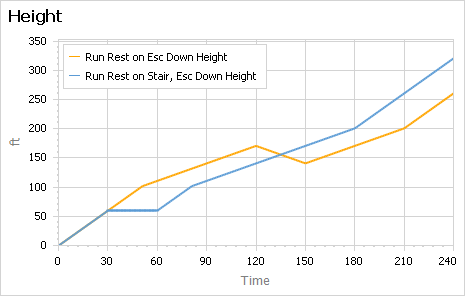
I suspect there are other interesting edge cases to explore.
The models:
Vensim (any version): Escalator 1.mdl
Vensim, alternate conception: Escalator 1 alt.mdl
Vensim Pro/DSS/Model Reader – subscripted for multiple experiments: escalator 2.mdl
Ventity: Escalator 1.zip
JJ Lauble has also created a version, posted at the Vensim forum. I haven’t had a chance to explore it yet, but it looks like he may have used Vensim to explore the algebraic solution, with the time axis as a way to scan the solution space with Synthesim overrides.