Biology Archives

Biological Dynamics of Stress Response

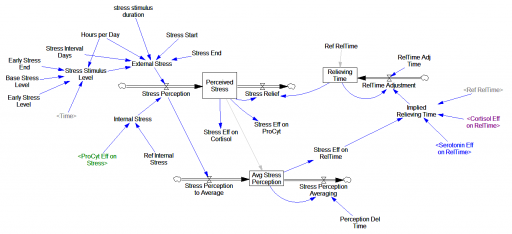
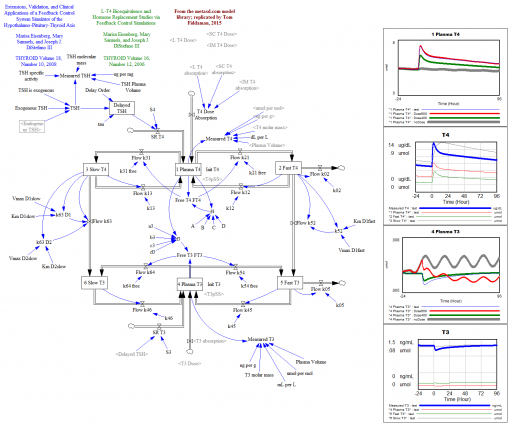
At ISDC 2018, we gave the Dana Meadows Award for best student paper to Gizem Aktas, for Modeling the Biological Mechanisms that Determine the Dynamics of Stress Response of the Human Body (with Yaman Barlas). This is a very interesting paper that elegantly synthesizes literature on stress, mood, and hormone interactions. I plan to write more about it later, but for the moment, here’s the model for your exploration.

The dynamic stress response of the human body to stressors is produced by nonlinear interactions among its physiological sub-systems. The evolutionary function of the response is to enable the body to cope with stress. However, depending on the intensity and frequency of the stressors, the mechanism may lose its function and the body can go into a pathological state. Three subsystems of the body play the most essential role in the stress response: endocrine, immune and neural systems. We constructed a simulation model of these three systems to imitate the stress response under different types of stress stimuli. Cortisol, glucocorticoid receptors, proinflammatory cytokines, serotonin, and serotonin receptors are the main variables of the model. Using both qualitative and quantitative physiological data, the model is structurally and behaviorally well-validated. In subsequent scenario runs, we have successfully replicated the development of major depression in the body. More interestingly, the model can present quantitative representation of some very well acknowledged qualitative hypotheses about the stress response of the body. This is a novel quantitative step towards the comprehension of stress response in relation with other disorders, and it provides us with a tool to design and test treatment methods.

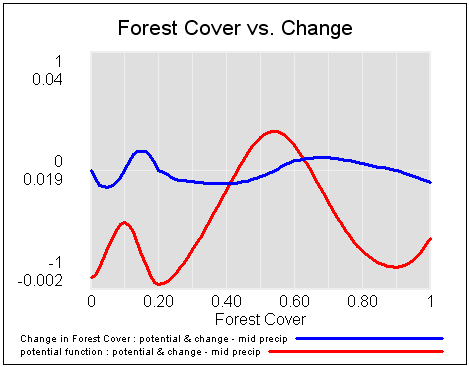
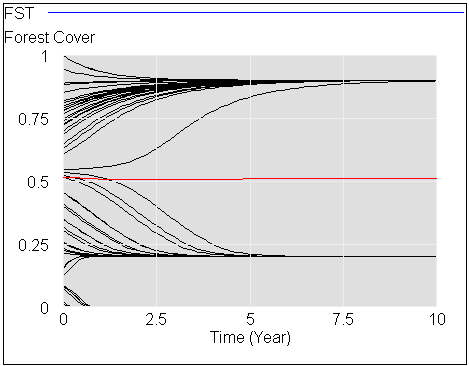
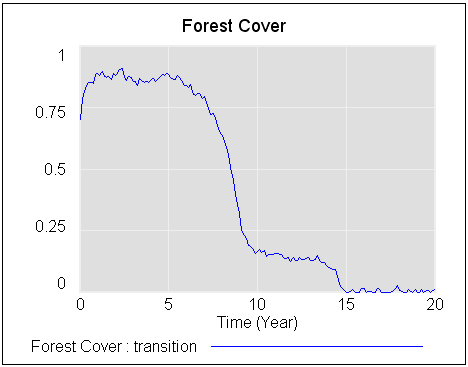
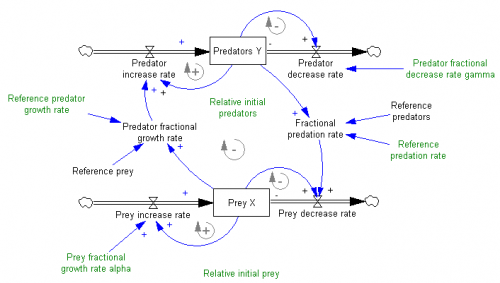
The original is a STELLA model; here I’ve translated it to Vensim and made some convenience upgrades. I used the forthcoming XMILE translation in Vensim to open the model. You get an ugly diagram (due to platform differences and XMILE’s lack of support for flow-clouds), but it’s functional enough to browse. I cleaned up the diagrams and moved them into multiple views to take better advantage of Vensim’s visual approach.

Continue reading “Biological Dynamics of Stress Response”

Thyroid Dynamics

Quite a while back, I posted about the dynamics of the thyroid and its interactions with other systems.

That was a conceptual model; this is a mathematical model. This is a Vensim replication of:

Marisa Eisenberg, Mary Samuels, and Joseph J. DiStefano III

Extensions, Validation, and Clinical Applications of a Feedback Control System Simulator of the Hypothalamo-Pituitary-Thyroid Axis

Background:We upgraded our recent feedback control system (FBCS) simulation model of human thyroid hormone (TH) regulation to include explicit representation of hypothalamic and pituitary dynamics, and up-dated TH distribution and elimination (D&E) parameters. This new model greatly expands the range of clinical and basic science scenarios explorable by computer simulation.

Methods: We quantified the model from pharmacokinetic (PK) and physiological human data and validated it comparatively against several independent clinical data sets. We then explored three contemporary clinical issues with the new model: …

… These results highlight how highly nonlinear feedback in the hypothalamic-pituitary-thyroid axis acts to maintain normal hormone levels, even with severely reduced TSH secretion.

THYROID
Volume 18, Number 10, 2008
DOI: 10.1089=thy.2007.0388

This version is a superset of the authors’ earlier 2006 model, and closely reproduces that with a few parameter changes.

L-T4 Bioequivalence and Hormone Replacement Studies via Feedback Control Simulations

THYROID
Volume 16, Number 12, 2006

The model is used in:

TSH-Based Protocol, Tablet Instability, and Absorption Effects on L-T4 Bioequivalence

THYROID
Volume 19, Number 2, 2009
DOI: 10.1089=thy.2008.0148

This works with any Vensim version:

thyroid 2008 d.mdl

thyroid 2008 d.vpm

Environmental Homeostasis

Replicated from

The Emergence of Environmental Homeostasis in Complex Ecosystems

The Earth, with its core-driven magnetic field, convective mantle, mobile lid tectonics, oceans of liquid water, dynamic climate and abundant life is arguably the most complex system in the known universe. This system has exhibited stability in the sense of, bar a number of notable exceptions, surface temperature remaining within the bounds required for liquid water and so a significant biosphere. Explanations for this range from anthropic principles in which the Earth was essentially lucky, to homeostatic Gaia in which the abiotic and biotic components of the Earth system self-organise into homeostatic states that are robust to a wide range of external perturbations. Here we present results from a conceptual model that demonstrates the emergence of homeostasis as a consequence of the feedback loop operating between life and its environment. Formulating the model in terms of Gaussian processes allows the development of novel computational methods in order to provide solutions. We find that the stability of this system will typically increase then remain constant with an increase in biological diversity and that the number of attractors within the phase space exponentially increases with the number of environmental variables while the probability of the system being in an attractor that lies within prescribed boundaries decreases approximately linearly. We argue that the cybernetic concept of rein control provides insights into how this model system, and potentially any system that is comprised of biological to environmental feedback loops, self-organises into homeostatic states.

See my related blog post for details.

Continue reading “Environmental Homeostasis”

Forest Cover Tipping Points

This is a model of forest stability and transitions, inspired by:

Global Resilience of Tropical Forest and Savanna to Critical Transitions

Marina Hirota, Milena Holmgren, Egbert H. Van Nes, Marten Scheffer

It has been suggested that tropical forest and savanna could represent alternative stable states, implying critical transitions at tipping points in response to altered climate or other drivers. So far, evidence for this idea has remained elusive, and integrated climate models assume smooth vegetation responses. We analyzed data on the distribution of tree cover in Africa, Australia, and South America to reveal strong evidence for the existence of three distinct attractors: forest, savanna, and a treeless state. Empirical reconstruction of the basins of attraction indicates that the resilience of the states varies in a universal way with precipitation. These results allow the identification of regions where forest or savanna may most easily tip into an alternative state, and they pave the way to a new generation of coupled climate models.

The paper is worth a read. It doesn’t present an explicit simulation model, but it does describe the concept nicely. I built the following toy model as a loose interpretation of the dynamics.

Some things to try:

Use a Synthesim override to replace Forest Cover with a ramp from 0 to 1 to see potentials and vector fields (rates of change), then vary the precipitation index to see how the stability of the forest, savanna and treeless states changes:

Start the system at different levels of forest cover (varying init forest cover), with default precipitation, to see the three stable attractors at zero trees, savanna (20% tree cover) and forest (90% tree cover):

Start with a stable forest, and a bit of noise (noise sd = .2 to .3), then gradually reduce precipitation (override the precipitation index with a ramp from 1 to 0) to see abrupt transitions in state:

There’s a more detailed discussion on my blog.

forest savanna treeless 1f.mdl (requires an advanced version of Vensim, or the free Model Reader)

forest savanna treeless 1f.vpm (ditto; includes a sensitivity file for varying the initial forest cover)

Lotka-Volterra predator-prey system

The Lotka-Volterra equations, which describe a predator-prey system, must be one of the more famous dynamic systems. There are many generalizations and applications outside of biology.

Wikipedia has a nice article, which I used as the basis for this simple model.

Continue reading “Lotka-Volterra predator-prey system”

A System Zoo

I just picked up a copy of Hartmut Bossel’s excellent System Zoo 1, which I’d seen years ago in German, but only recently discovered in English. This is the first of a series of books on modeling – it covers simple systems (integration, exponential growth and decay), logistic growth and variants, oscillations and chaos, and some interesting engineering systems (heat flow, gliders searching for thermals). These are high quality models, with units that balance, well-documented by the book. Every one I’ve tried runs in Vensim PLE so they’re great for teaching.

I haven’t had a chance to work my way through the System Zoo 2 (natural systems – climate, ecosystems, resources) and System Zoo 3 (economy, society, development), but I’m pretty confident that they’re equally interesting.

You can get the models for all three books, in English, from the Uni Kassel Center for Environmental Systems Research – it’s now easy to find a .zip archive of the zoo models for the whole series, in Vensim .mdl format, on CESR’s home page: www2.cesr.de/downloads.

To tantalize you, here are some images of model output from Zoo 1. First, a phase map of a bistable oscillator, which was so interesting that I built one with my kids, using legos and neodymium magnets:

Continue reading “A System Zoo”

Fibonacci Rabbits

This is a small, discrete time model that explores the physical interpretation of the Fibonacci sequence. See my blog post about this model for details.

Fibonacci2.vpm This runs with Vensim PLE, but users might want to use the Model Reader in order to load the included .cin file with non-growing eigenvector settings.

Bifurcating Salmon

A nifty paper on nonlinear dynamics of salmon populations caught my eye on ArXiv.org today. The math is straightforward and elegant, so I replicated the model in Vensim.

A three-species model explaining cyclic dominance of pacific salmon

Authors: Christian Guill, Barbara Drossel, Wolfram Just, Eddy Carmack

Abstract: The four-year oscillations of the number of spawning sockeye salmon (Oncorhynchus nerka) that return to their native stream within the Fraser River basin in Canada are a striking example of population oscillations. The period of the oscillation corresponds to the dominant generation time of these fish. Various – not fully convincing – explanations for these oscillations have been proposed, including stochastic influences, depensatory fishing, or genetic effects. Here, we show that the oscillations can be explained as a stable dynamical attractor of the population dynamics, resulting from a strong resonance near a Neimark Sacker bifurcation. This explains not only the long-term persistence of these oscillations, but also reproduces correctly the empirical sequence of salmon abundance within one period of the oscillations. Furthermore, it explains the observation that these oscillations occur only in sockeye stocks originating from large oligotrophic lakes, and that they are usually not observed in salmon species that have a longer generation time.

The paper does a nice job of connecting behavior to structure, and of relating the emergence of oscillations to eigenvalues in the linearized system.

Units balance, though I had to add a couple implicit scale factors to do so.

The general results are qualitatitively replicable. I haven’t tried to precisely reproduce the authors’ bifurcation diagram and other experiments, in part because I couldn’t find a precise specification of numerical methods used (time step, integration method), so I wouldn’t expect to succeed.

Unlike most SD models, this is a hybrid discrete-continuous system. Salmon, predator and zooplankton populations evolve continuously during a growing season, but with discrete transitions between seasons.

The model uses SAMPLE IF TRUE, so you need an advanced version of Vensim to run it, or the free Model Reader. (It should be possible to replace the SAMPLE IF TRUE if an enterprising person wanted a PLE version). It would also be a good candidate for an application of SHIFT IF TRUE if someone wanted to experiment with the cohort age structure.

sockeye.vmf

For a more policy-oriented take on salmon, check out Andy Ford’s work on smolt migration.

Logistic Chaos

This is an implementation of the logistic model – a very simple example of discrete time chaotic behavior. It’s sometimes used to illustrate chaotic dynamics of insect populations.

There’s a nice description here, and the other top links on google tend to be good.

Note that this version corrects an equation error in previous versions.

Logistic (Vensim .vpm)

Logistic (Vensim .vmf)

Ultradian Oscillations of Insulin and Glucose

Citation: Jeppe Sturis, Kenneth S. Polonsky, Erik Mokilde, and Eve van Cauter. Computer Model for Mechanisms Underlying Ultradian Oscillations of Insulin and Glucose. Am. J. Physiol. 260 (Endocrinol. Metab. 23): E801-E809, 1991.

Source: Replicated by Hank Taylor

Units: No Yes!

Format: Vensim

Ultradian Oscillations of Insulin and Glucose (Vensim .vpm)

Update, 10/2017:

Refreshed, with units defined (mathematically the same as before): ultradia2.vpm ultradia2.mdl

Further refined, for initialization in equilibrium (insulin by analytic expression; glucose by parameter). Glucose infusion turned on by default. Graphs added.

ultradia-enhanced-3.mdl ultradia-enhanced-3.vpm