There are warning signs when the active structure of a system is changing. But a new paper shows that they may not always be helpful for averting surprise catastrophes.
Catastrophic Collapse Can Occur without Early Warning: Examples of Silent Catastrophes in Structured Ecological Models (PLOS ONE – open access)
Catastrophic and sudden collapses of ecosystems are sometimes preceded by early warning signals that potentially could be used to predict and prevent a forthcoming catastrophe. Universality of these early warning signals has been proposed, but no formal proof has been provided. Here, we show that in relatively simple ecological models the most commonly used early warning signals for a catastrophic collapse can be silent. We underpin the mathematical reason for this phenomenon, which involves the direction of the eigenvectors of the system. Our results demonstrate that claims on the universality of early warning signals are not correct, and that catastrophic collapses can occur without prior warning. In order to correctly predict a collapse and determine whether early warning signals precede the collapse, detailed knowledge of the mathematical structure of the approaching bifurcation is necessary. Unfortunately, such knowledge is often only obtained after the collapse has already occurred.
To get the insight, it helps to back up a bit. (If you haven’t read my posts on bifurcations and 1D vector fields, they’re good background for this.)
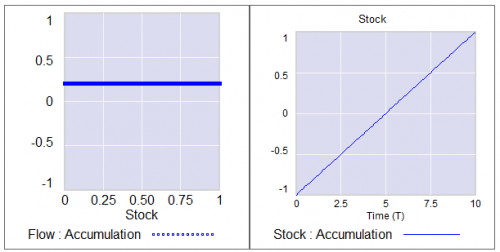
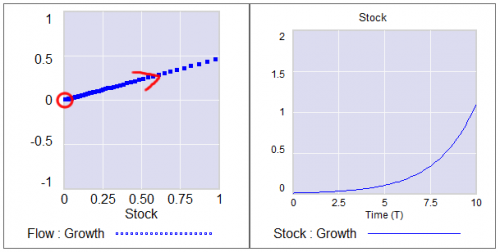
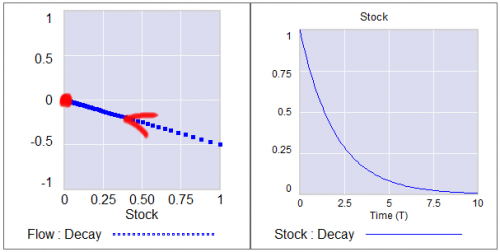
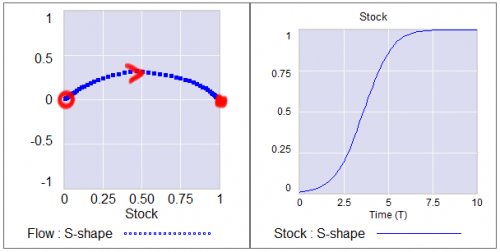
Consider a first order system, with a flow that is a sinusoid, plus noise:
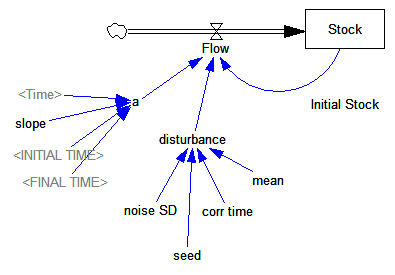
Flow=a*SIN(Stock*2*pi) + disturbance
For different values of a, and disturbance = 0, this looks like:
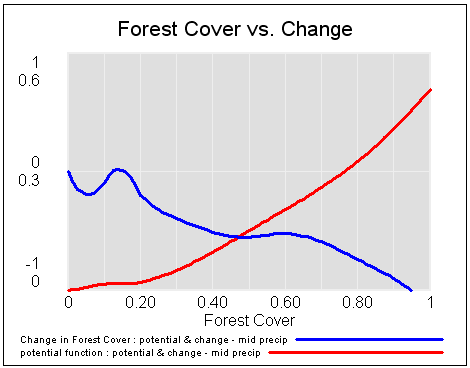
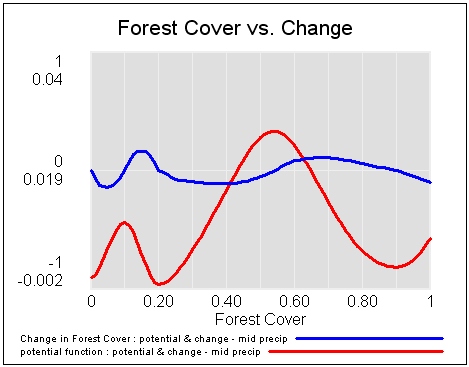
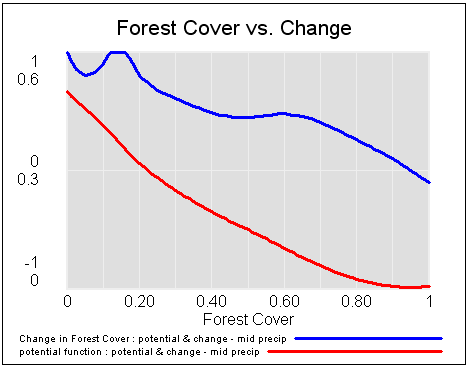
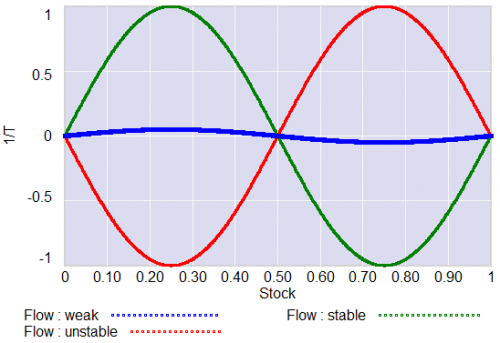 For a = 1, the system has a stable point at stock=0.5. The gain of the negative feedback that maintains the stable point at 0.5, given by the slope of the stock-flow phase plot, is strong, so the stock will quickly return to 0.5 if disturbed.
For a = 1, the system has a stable point at stock=0.5. The gain of the negative feedback that maintains the stable point at 0.5, given by the slope of the stock-flow phase plot, is strong, so the stock will quickly return to 0.5 if disturbed.
For a = -1, the system is unstable at 0.5, which has become a tipping point. It’s stable at the extremes where the stock is 0 or 1. If the stock starts at 0.5, the slightest disturbance triggers feedback to carry it to 0 or 1.
For a = 0.04, the system is approaching the transition (i.e. bifurcation) between stable and unstable behavior around 0.5. The gain of the negative feedback that maintains the stable point at 0.5, given by the slope of the stock-flow phase plot, is weak. If something disturbs the system away from 0.5, it will be slow to recover. The effective time constant of the system around 0.5, which is inversely proportional to a, becomes long for small a. This is termed critical slowing down.
For a=0 exactly, not shown, there is no feedback and the system is a pure random walk that integrates the disturbance.
The neat thing about critical slowing down, or more generally the approach of a bifurcation, is that it leaves fingerprints. Here’s a run of the system above, with a=1 (stable) initially, and ramping to a=-.33 (tipping) finally. It crosses a=0 (the bifurcation) at T=75. The disturbance is mild pink noise.
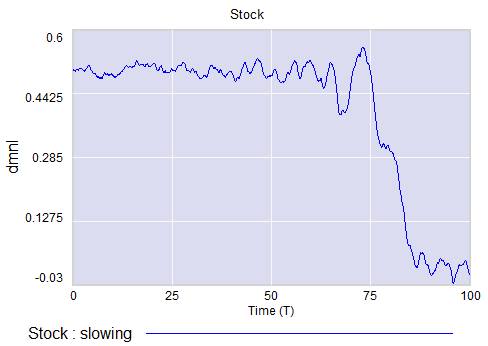
Notice that, as a approaches zero, particularly between T=50 and T=75, the variance of the stock increases considerably.
This means that you can potentially detect approaching bifurcations in time series without modeling the detailed interactions in the system, by observing the variance or similar, better other signs. Such analyses indicate that there has been a qualitative change in Arctic sea ice behavior, for example.
Now, back to the original paper.
It turns out that there’s a catch. Not all systems are neatly one dimensional (though they operate on low-dimensional manifolds surprisingly often).
In a multidimensional phase space, the symptoms of critical slowing down don’t necessarily reveal themselves in all variables. They have a preferred orientation in the phase space, associated with the eigenvectors of the eigenvalue that’s changing at the bifurcation.
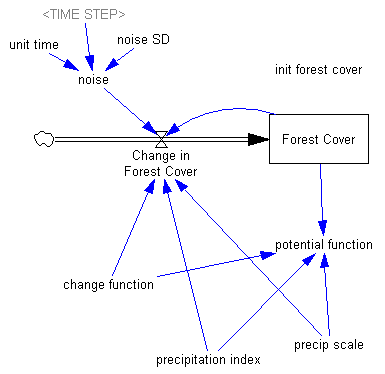
The authors explore a third-order ecological model with juvenile and adult prey and a predator:
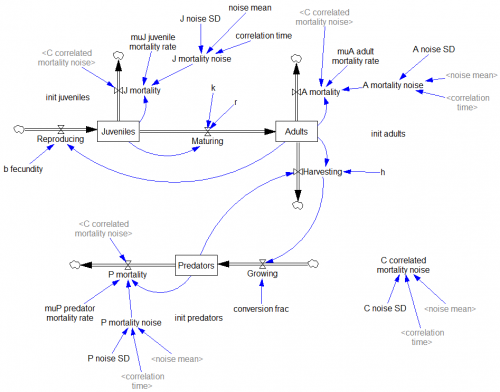
Predators undergo a collapse when their mortality rate exceeds a critical value (.553). Here, I vary the mortality rate gradually from .55 to .56, with the collapse occurring around time 450:
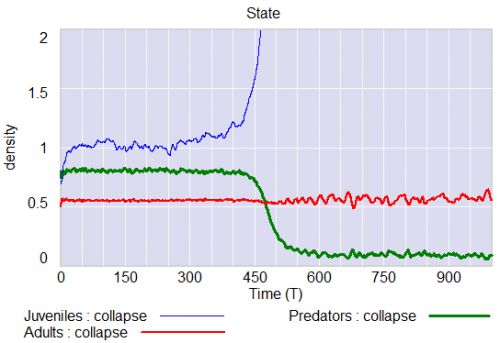
Note that the critical value of the mortality rate is actually passed around time 300, so it takes a while for the transient collapse to occur. Also notice that the variance of the adult population changes a lot post-collapse. This is another symptom of qualitative change in the dynamics.
The authors show that, in this system, approaching criticality of the predator mortality rate only reveals itself in increased variance or autocorrelation if noise impacts the juvenile population, and even then you have to be able to see the juvenile population.
We have shown three examples where catastrophic collapse can occur without prior early warning signals in autocorrelation or variance. Although critical slowing down is a universal property of fold bifurcations, this does not mean that the increased sensitivity will necessarily manifest itself in the system variables. Instead, whether the population numbers will display early warning will depend on the direction of the dominant eigenvector of the system, that is, the direction in which the system is destabilizing. This theoretical point also applies to other proposed early warning signals, such as skewness [18], spatial correlation [19], and conditional heteroscedasticity [20]. In our main example, early warning signal only occurs in the juvenile population, which in fact could easily be overlooked in ecological systems (e.g. exploited, marine fish stocks), as often only densities of older, more mature individuals are monitored. Furthermore, the early warning signals can in some cases be completely absent, depending on the direction of the perturbations to the system.
They then detail some additional reasons for lack of warning in similar systems.
In conclusion, we propose to reject the currently popular hypothesis that catastrophic shifts are preceded by universal early warning signals. We have provided counterexamples of silent catastrophes, and we have pointed out the underlying mathematical reason for the absence of early warning signals. In order to assess whether specific early warning signals will occur in a particular system, detailed knowledge of the underlying mathematical structure is necessary.
In other words, critical slowing down is a convenient, generic sign of impending change in a time series, but its absence is not a reliable indicator that all is well. Without some knowledge of the system in question, surprise can easily occur.
I think one could further strengthen the argument against early warning by looking at transients. In my simulation above, I’d argue that it takes at least 100 time units to detect a change in the variance of the juvenile population with any confidence, after it passes the critical point around T=300 (longer, if someone’s job depends on not seeing the change). The period of oscillations of the adult population in response to a disturbance is about 20 time units. So it seems likely that early warning, even where it exists, can only be established on time scales that are long with respect to the natural time scale of the system and environmental changes that affect it. Therefore, while signs of critical slowing down might exist in principle, they’re not particularly useful in this setting.
The models are in my library.
Catastrophic Collapse Can Occur without Early Warning: Examples of Silent Catastrophes in Structured Ecological Models


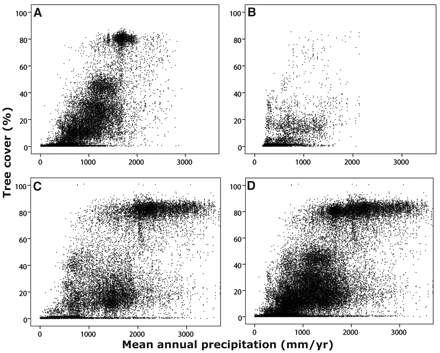
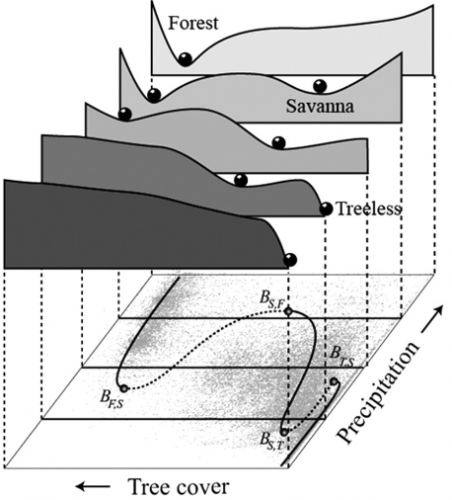
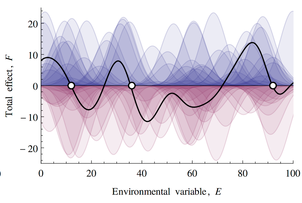 If this looks familiar, there’s a reason. What’s happening along the E dimension is a lot like what happens along the time dimension in
If this looks familiar, there’s a reason. What’s happening along the E dimension is a lot like what happens along the time dimension in 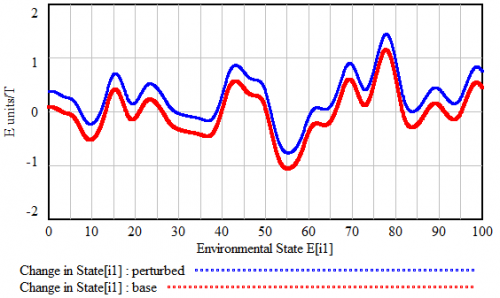
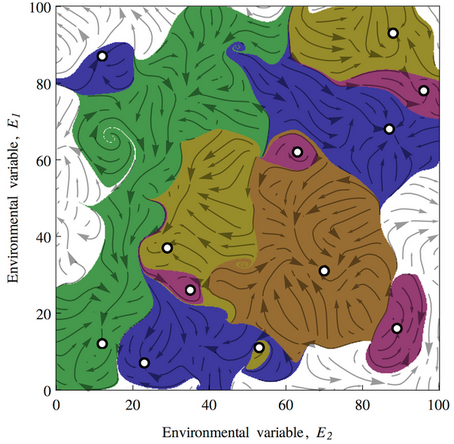 This leads to a variety of conclusions about ecological stability, for which I encourage you to have a look at the full paper. It’s interesting to ponder the applicability and implications of this conceptual model for social systems.
This leads to a variety of conclusions about ecological stability, for which I encourage you to have a look at the full paper. It’s interesting to ponder the applicability and implications of this conceptual model for social systems.




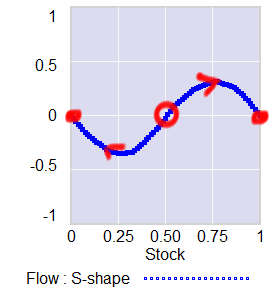
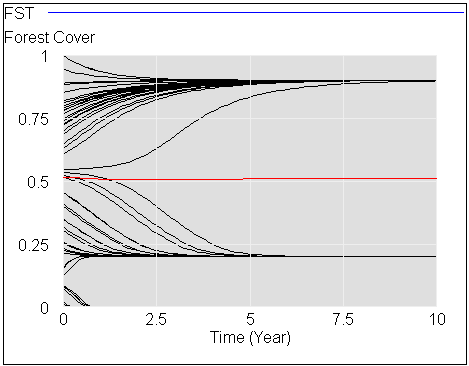
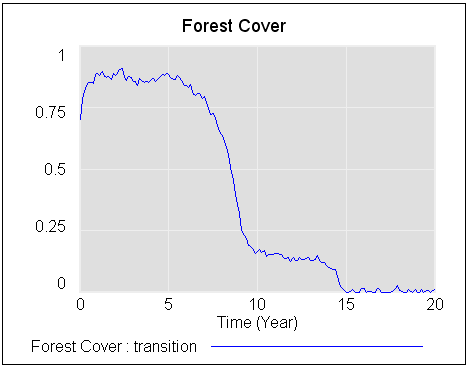
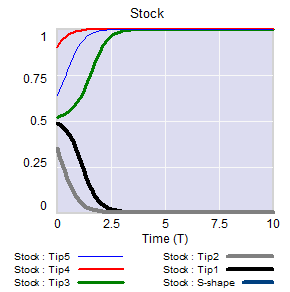 If the stock starts out near 1, it will stay there fairly robustly, because feedback will restore that state from any excursion. But if some intervention or noise pushes the stock below 0.5, feedback will then draw it toward 0. Once there, it will be fairly robustly stuck again. This behavior can be surprising and disturbing if 1=good and 0=bad.
If the stock starts out near 1, it will stay there fairly robustly, because feedback will restore that state from any excursion. But if some intervention or noise pushes the stock below 0.5, feedback will then draw it toward 0. Once there, it will be fairly robustly stuck again. This behavior can be surprising and disturbing if 1=good and 0=bad.
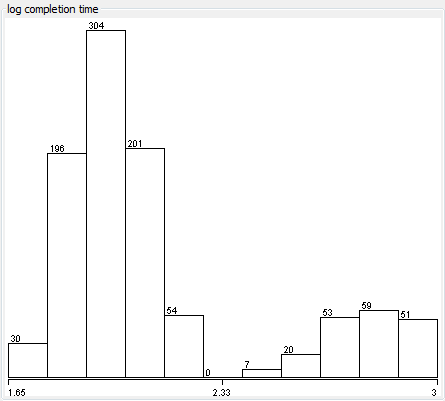

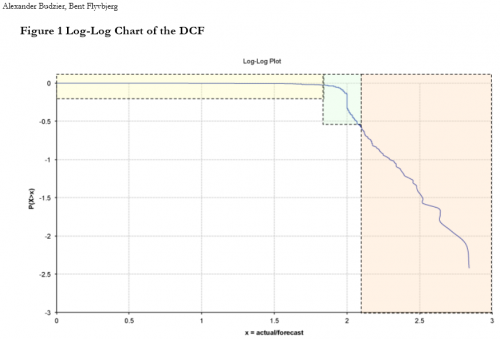
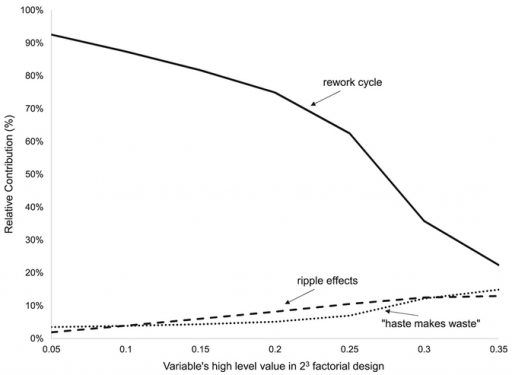
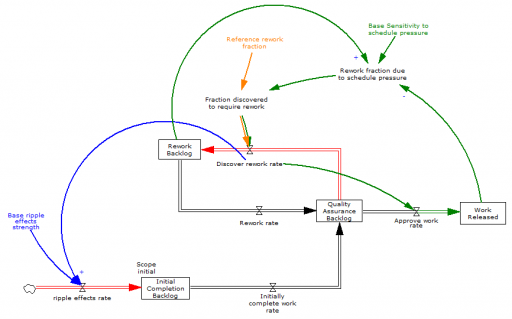
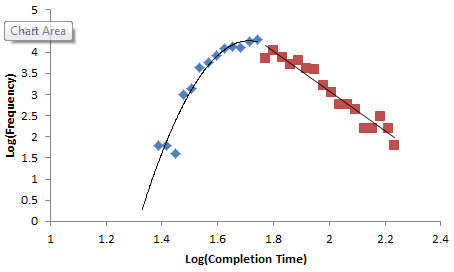 Normal+uniformly-distributed uncertainty in project estimation, productivity and ripple/rework effects generates a lognormal-ish left tail (parabolic on the log-log axes above) and a heavy Power Law right tail.
Normal+uniformly-distributed uncertainty in project estimation, productivity and ripple/rework effects generates a lognormal-ish left tail (parabolic on the log-log axes above) and a heavy Power Law right tail.