Don't just do something, stand there! Reflections on the counterintuitive behavior of complex systems, seen through the eyes of System Dynamics, Systems Thinking and simulation.
In this case, I think it’s quite literally Normal a.k.a. Gaussian:
Here’s what I think is happening. On windless days with powder, the snow dribbles off the edge of the roof (just above the center of the hump). Flakes drift down in a random walk. The railing terminates the walk after about four feet, by which time the distribution of flake positions has already reached the Normal you’d expect from the Central Limit Theorem.
Enough of the geek stuff; I think I’ll go ski the field.
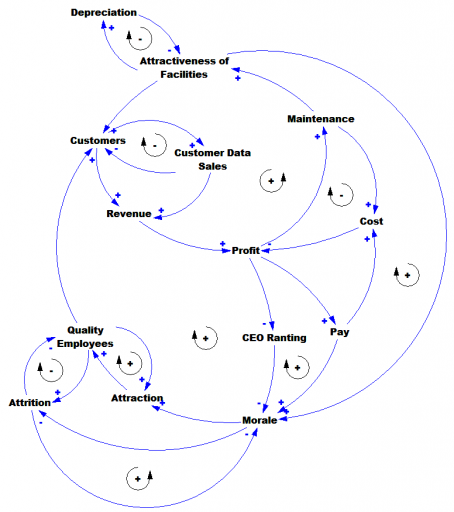
I just published three short videos with sample models, illustrating representation of discrete and random events in Vensim.
Jay Forrester‘s advice from Industrial Dynamics is still highly relevant. Here’s an excerpt:
Chapter 5, Principles for Formulating Models
5.5 Continuous Flows
In formulating a model of an industrial operation, we suggest that the system be treated, at least initially, on the basis of continuous flows and interactions of the variables. Discreteness of events is entirely compatible with the concept of information-feedback systems, but we must be on guard against unnecessarily cluttering our formulation with the detail of discrete events that only obscure the momentum and continuity exhibited by our industrial systems.
In beginning, decisions should be formulated in the model as if they were continuously (but not implying instantaneously) responsive to the factors on which they are based. This means that decisions will not be formulated for intermittent reconsideration each week, month or year. For example, factory production capacity would vary continuously, not by discrete additions. Ordering would go on continuously, not monthly when the stock records are reviewed.
There are several reasons for recommending the initial formulation of a continuous model:
These comments should never be construed as suggesting that the model builder should lack interest in the microscopic separate events that occur in a continuous-flow channel. The course of the continuous flow is the course of the separate events in it. By studying individual events we get a picture of how decisions are made and how the flows are delayed. The study of individual events is on of our richest sources of information about the way the flow channels of the model should be constructed. When a decision is actually being made regularly on a periodic basis, like once a month, the continuous-flow equivalent channel should contain a delay of half the interval; this represents the average delay encountered by information in the channel.
The preceding comments do not imply that discreteness is difficult to represent, nor that it should forever be excluded from a model. At times it will become significant. For example, it may create a disturbance that will cause system fluctuations that can be mistakenly interreted as externally generated cycles (…). When a model has progressed to the point where such refinements are justified, and there is reason to believe that discreteness has a significant influence on system behavior, discontinuous variables should then be explored to determine their effect on the model.
[Ellipses added – see the original for elaboration.]
A conversation about infrastructure, with Carter Williams of iSelect and me:
The $3 Trillion Problem: Solving America’s Infrastructure Crisis
I can’t believe I forgot to mention one of the most obvious System Dynamics insights about infrastructure:
There are two ways to fill a leaky bucket – increase the inflow, or plug the outflows. There’s always lots of enthusiasm for increasing the inflow by building new stuff. But there’s little sense in adding to the infrastructure stock if you can’t maintain what you have. So, plug the leaks first, and get into a proactive maintenance mode. Then you can have fun building new things – if you can afford it.
Sears Roebuck & Co. was a big part of my extended family at one time. My wife’s grandfather started in the mail room and worked his way up to executive, through the introduction of computers and the firebombing in Caracas. Sadly, its demise appears imminent.
Business Insider has an interesting article on the dynamics of Sears’ decline. Here’s a quick causal loop diagram summarizing some of the many positive feedbacks that once drove growth, but now are vicious cycles:
h/t @johnrodat
CLD corrected, 1/9/17.