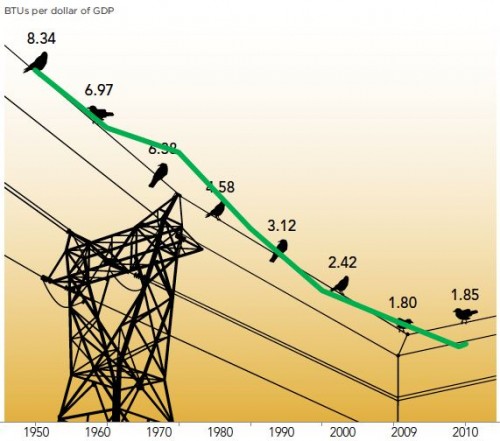
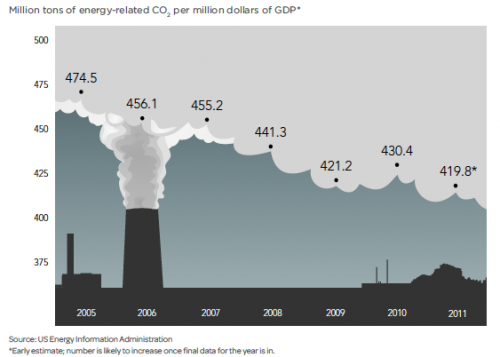
The President said, in the State of the Union Address,
We have a supply of natural gas that can last America nearly one hundred years, and my Administration will take every possible action to safely develop this energy.
The 100 year figure presumably comes straight from EIA:
According to the EIA Annual Energy Outlook 2011, the United States possesses 2,543 trillion cubic feet (Tcf) of potential natural gas resources. Natural gas from shale resources, considered uneconomical just a few years ago, accounts for 862 Tcf of this resource estimate. At the 2010 rate of U.S. consumption (about 24.1 Tcf per year), 2,543 Tcf of natural gas is enough to supply over 100 years of use.
100 years is the static reserve life index (SRLI). It’s well known that the SRLI is a misleading metric (this figured prominently in Limits to Growth, for example). Exponential growth in consumption violates the basic assumption of the SRLI, which is that consumption remains constant. Even a small amount of growth greatly erodes the actual lifetime of a resource:
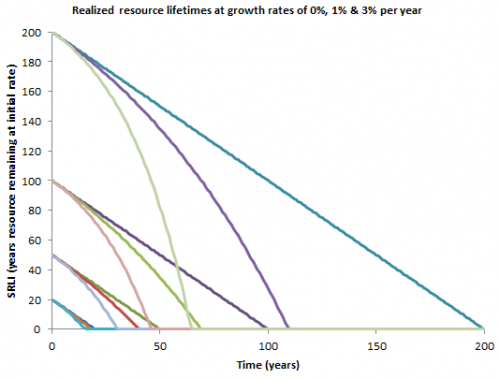 Growth at 3% per year reduces the SRLI of gas from 100 years to a realized lifetime of 45 years, which is not nearly so comfortable. This ought to be intuitive even if you can’t integrate exponentials in your head, because gas consumption would have to roughly double to replace coal (and that doubling would have to happen quickly to meet job claims), so clearly “100 years at current rates” isn’t going to happen.
Growth at 3% per year reduces the SRLI of gas from 100 years to a realized lifetime of 45 years, which is not nearly so comfortable. This ought to be intuitive even if you can’t integrate exponentials in your head, because gas consumption would have to roughly double to replace coal (and that doubling would have to happen quickly to meet job claims), so clearly “100 years at current rates” isn’t going to happen.
Update: EIA just lowered shale gas resource estimates by nearly half, taking another big bite out of the SRLI:
In the AEO2012 Reference case, the estimated unproved technically recoverable resource (TRR) of shale gas for the United States is 482 trillion cubic feet, substantially below the estimate of 827 trillion cubic feet in AEO2011.