A question about sigmoid functions prompted me to collect a lot of small models that I’ve used over the years.
A sigmoid function is just a function with a characteristic S shape. (OK, you have to use your imagination a bit to get the S.) These tend to arise in two different ways:
- As a nonlinear response, where increasing the input initially has little effect, then considerable effect, then saturates with little effect. Neurons, and transfer functions in neural networks, behave this way. Advertising is also thought to work like this: too little, and people don’t notice. Too much, and they become immune. Somewhere in the middle, they’re responsive.
- Dynamically, as the behavior over time of a system with shifting dominance from growth to saturation. Examples include populations approaching carrying capacity and the Bass diffusion model.
Correspondingly, there are (at least) two modeling situations that commonly require the use of some kind of sigmoid function:
- You want to represent the kind of saturating nonlinear effect described above, with some parameters to control the minimum and maximum values, the slope around the central point, and maybe symmetry features.
- You want to create a simple scenario generator for some driver of your model that has logistic behavior, but you don’t want to bother with an explicit dynamic structure.
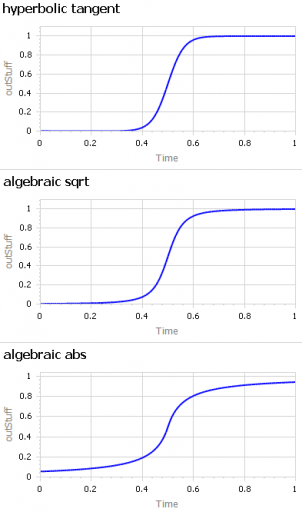
The examples in this model address both needs. They include:
- logistic and generalized logistic dynamic structures and functions
- normalization of lookups
- scaling and range-setting
- use of a Beta-like distribution to construct a sigmoid
- hyperbolic tangent and other simple functions
- functions defined from (0,0) to (1,1)
I’m sure there are still a lot of alternatives I omitted. Cubic splines and Bezier curves come to mind. I’d be interested to hear of any others of interest, or just alternative parameterizations of things already here.
The model:
Vensim: sigmoids 1.mdl (works in PLE, Pro, DSS)
Ventity: Sigmoids 1.zip
