The following models are replicated from Steven Strogatz’ excellent text, Nonlinear Dynamics and Chaos.
These are just a few of the many models in the text. They illustrate bifurcations in one-dimensional systems (saddle node, transcritical, pitchfork) and one two-dimensional system (Hopf). The pitchfork bifurcation is closely related to the cusp catastrophe in the climate model recently posted.
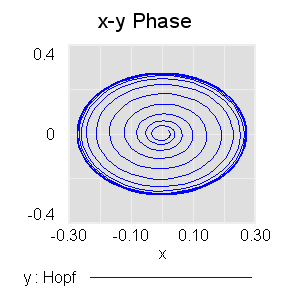
Spiral from a point near the unstable fixed point at the origin to a stable limit cycle after a Hopf bifurcation (mu=.075, r0 = .025)
These are in support of an upcoming post on bifurcations and tipping points, so I won’t say more at the moment. I encourage you to read the book. If you replicate more of the models in it, I’d love to have copies here.
These are systems in normal form and therefore dimensionless and lacking in physical interpretation, though they certainly crop up in many real-world systems.
3-1 saddle node bifurcation.mdl
3-2 transcritical bifurcation.mdl
Update: A related generic model illustrating critical slowing down:

2 thoughts on “Bifurcations from Strogatz’ Nonlinear Dynamics and Chaos”