An interesting article in PLOS one explores the consequences of a system of random feedbacks:
The Emergence of Environmental Homeostasis in Complex Ecosystems
The Earth, with its core-driven magnetic field, convective mantle, mobile lid tectonics, oceans of liquid water, dynamic climate and abundant life is arguably the most complex system in the known universe. This system has exhibited stability in the sense of, bar a number of notable exceptions, surface temperature remaining within the bounds required for liquid water and so a significant biosphere. Explanations for this range from anthropic principles in which the Earth was essentially lucky, to homeostatic Gaia in which the abiotic and biotic components of the Earth system self-organise into homeostatic states that are robust to a wide range of external perturbations. Here we present results from a conceptual model that demonstrates the emergence of homeostasis as a consequence of the feedback loop operating between life and its environment. Formulating the model in terms of Gaussian processes allows the development of novel computational methods in order to provide solutions. We find that the stability of this system will typically increase then remain constant with an increase in biological diversity and that the number of attractors within the phase space exponentially increases with the number of environmental variables while the probability of the system being in an attractor that lies within prescribed boundaries decreases approximately linearly. We argue that the cybernetic concept of rein control provides insights into how this model system, and potentially any system that is comprised of biological to environmental feedback loops, self-organises into homeostatic states.
To get a handle on how this works, I replicated the model (see my library).
The basic mechanism of the model is rein control, in which multiple unidirectional forces on a system act together to yield bidirectional feedback control. By analogy, the reins on a horse can only pull in one direction, but with a pair of reins, it’s possible to turn both left and right.
In the model, there’s a large random array of reins, consisting of biotic feedbacks that occur near a particular system state. In the simple one-dimensional case, when you add a bunch of these up, you get a 1D vector field that looks like this:
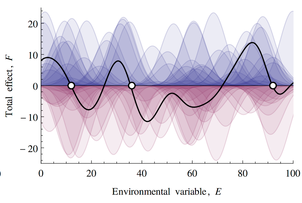 If this looks familiar, there’s a reason. What’s happening along the E dimension is a lot like what happens along the time dimension in pink noise: at any given point, the sum of a lot of random impulses yield a wiggly net response, with a characteristic scale yielded by the time constant (pink noise) or niche width of biotic components (rein control).
If this looks familiar, there’s a reason. What’s happening along the E dimension is a lot like what happens along the time dimension in pink noise: at any given point, the sum of a lot of random impulses yield a wiggly net response, with a characteristic scale yielded by the time constant (pink noise) or niche width of biotic components (rein control).
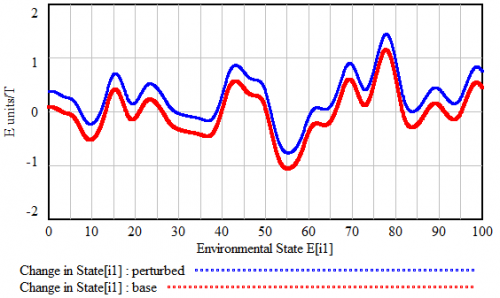
What this yields is an alternating series of unstable (tipping) points and stable equilibria. When the system is perturbed by some external force, the disturbance shifts the aggregate response, as below. Generally, a few stable points may disappear, but the large features of the landscape are preserved, so the system resists the disturbance.
 With a higher-dimensional environmental state, this creates convoluted basins of attraction:
With a higher-dimensional environmental state, this creates convoluted basins of attraction:
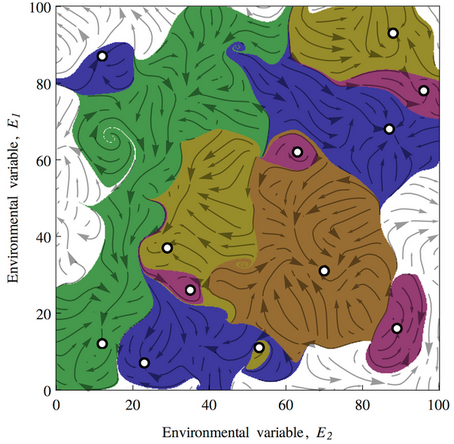 This leads to a variety of conclusions about ecological stability, for which I encourage you to have a look at the full paper. It’s interesting to ponder the applicability and implications of this conceptual model for social systems.
This leads to a variety of conclusions about ecological stability, for which I encourage you to have a look at the full paper. It’s interesting to ponder the applicability and implications of this conceptual model for social systems.

Nice find Tom.
“It’s interesting to ponder the applicability and implications of this conceptual model for social systems.”
Indeed, just look that the instability we’ve seen with a shrinking pool of people participating in politics!
On the topic of politics, this is an interesting model:
http://www.pnas.org/content/104/18/7351.abstract