The vision of teacher value added modeling (VAM) is a good thing: evaluate teachers based on objective measures of their contribution to student performance. It may be a bit utopian, like the cybernetic factory, but I’m generally all for substitution of reason for baser instincts. But a prerequisite for a good control system is a good model connected to adequate data streams. I think there’s reason to question whether we have these yet for teacher VAM.
The VAM models I’ve seen are all similar. Essentially you do a regression on student performance, with a dummy for the teacher, and as many other explanatory variables as you can think of. Teacher performance is what’s left after you control for demographics and whatever else you can think of. (This RAND monograph has a useful summary.)
Right away, you can imagine lots of things going wrong. Statistically, the biggies are omitted variable bias and selection bias (because students aren’t randomly assigned to teachers). You might hope that omitted variables come out in the wash for aggregate measurements, but that’s not much consolation to individual teachers who could suffer career-harming noise. Selection bias is especially troubling, because it doesn’t come out in the wash. You can immediately think of positive-feedback mechanisms that would reinforce the performance of teachers who (by mere luck) perform better initially. There might also be nonlinear interaction affects due to classroom populations that don’t show up as the aggregate of individual student metrics.
On top of the narrow technical issues are some bigger philosophical problems with the measurements. First, they’re just what can be gleaned from standardized testing. That’s a useful data point, but I don’t think I need to elaborate on its limitations. Second, the measurement is a one-year snapshot. That means that no one gets any credit for building foundations that enhance learning beyond a single school year. We all know what kind of decisions come out of economic models when you plug in a discount rate of 100%/yr.
The NYC ed department claims that the models are good:
Q: Is the value-added approach reliable?
A: Our model met recognized standards for validity and reliability. Teachers’ value-added scores were positively correlated with school Progress Report scores and principals’ evaluations of teacher effectiveness. A teacher’s value-added score was highly stable from year to year, and the results for teachers in the top 25 percent and bottom 25 percent were particularly stable.
That’s odd, because independent analysis by Gary Rubinstein of FOI released data indicates that scores are highly unstable. I found that hard to square with the district’s claims about the model, above, so I did my own spot check:
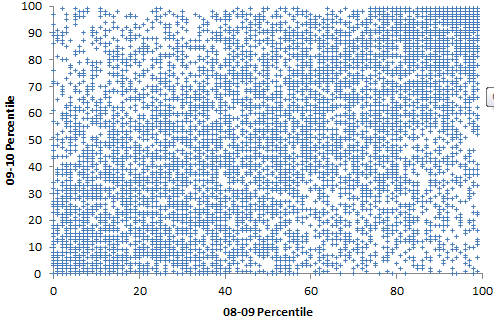 Percentiles are actually not the greatest measure here, because they throw away a lot of information about the distribution. Also, the points are integers and therefore overlap. Here are raw z-scores:
Percentiles are actually not the greatest measure here, because they throw away a lot of information about the distribution. Also, the points are integers and therefore overlap. Here are raw z-scores:
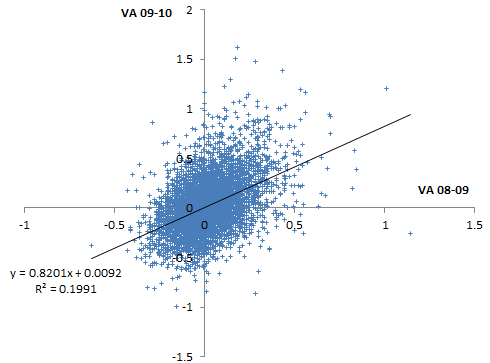 Some things to note here:
Some things to note here:
- There is at least some information here.
- The noise level is very high.
- There’s no visual evidence of the greater reliability in the tails cited by the district. (Unless they’re talking about percentiles, in which case higher reliability occurs almost automatically, because high ranks can only go down, and ranking shrinks the tails of the distribution.)
The model methodology is documented in a memo. Unfortunately, it’s a typical opaque communication in Greek letters, from one statistician to another. I can wade through it, but I bet most teachers can’t. Worse, it’s rather sketchy on model validation. This isn’t just research, it’s being used for control. It’s risky to put a model in such a high-stakes, high profile role without some stress testing. The evaluation of stability in particular (pg. 21) is unsatisfactory because the authors appear to have reported it at the performance category level rather than the teacher level, when the latter is the actual metric of interest, upon which tenure decisions will be made. Even at the category level, cross-year score correlations are very low (~.2-.3) in English and low (~.4-.6) in math (my spot check results are even lower).
What’s really needed here is a full end-to-end model of the system, starting with a synthetic data generator, replicating the measurement system (the 3-tier regression), and ending with a population model of teachers. That’s almost the only way to know whether VAM as a control strategy is really working for this system, rather than merely exercising noise and bias or triggering perverse side effects. The alternative (which appears to be underway) is the vastly more expensive option of experimenting with real $ and real people, and I bet there isn’t adequate evaluation to assess the outcome properly.
Because it does appear that there’s some information here, and the principle of objective measurement is attractive, VAM is an experiment that should continue. But given the uncertainties and spectacular noise level in the measurements, it should be rolled out much more gradually. It’s bonkers for states to hang 50% of a teacher’s evaluation on this method. It’s quite ironic that states are willing to make pointed personnel decisions on the basis of such sketchy information, when they can’t be moved by more robust climate science.
Really, the thrust here ought to have two prongs. Teacher tenure and weeding out the duds ought to be the smaller of the two. The big one should be to use this information to figure out what makes better teachers and classrooms, and make them.

While I agree in the abstract with all of your statistical concerns and tend to agree with your Burkean notion that the rollout should be more gradual, it seems like what’s sorely missing from the assessments is model comparison: do human raters (with baser instincts) not suffer from omitted variable bias? And are their ratings more consistent across years? Are people actually performing this comparison?
Good discussion.
Because I work in arts education, I am acutely aware of the reification of scores on standardized tests in evaluating students and teachers. Such tests are designed to sample learning that conforms to standards. Of course, the fidelity of tests to the standards under consideration is not really questioned very often. I understand that the alignment of tests with standards is really low (see Andrew Porter’s work). In any case, standardized tests in just a few subjects are being treated as if prototypes for all subjects. And, all value-added measures support outcome-based rationales for education, as if resources available for teaching did not matter, and as if the relative advantages of some students can be fully counted, nicely weighted, and factored into algorithms (or given the status of a random variation).
A preoccupation with the niceties of statistics is blinding a lot of people to the distortions of educational processes, products, and contexts that these number-crunching exercises require and are propagating. Among these distortions are such huge investments in time and money for testing that teaching is becoming ancillary to gathering information that can be crunched, squeezed, distilled, reduced to a number.
In value-added measures of teacher quality, statisticians assume that everything worth knowing about teaching and learning can be accounted for, or if not, treated as if randomly distributed. These fictions are also sustained in observation protocols that portray “highly effective” teachers as hired hands who succeed in delivering instruction in a pre-determined sequence and at a rate that brings every student into the mythic realm of being “at or above grade level” in less than nine months…consistently, from year to year.
In any case, it would be useful and truthful for persons who are promoting “value-added” estimates of teacher quality to affirm that these statistical models migrated into the center of educational policies from studies of genetic engineering in agriculture. The studies and stats in that field are typically used to propagate superior traits through selective breeding, to accelerate genetic improvements, and to engineer transformations with new features (e.g., capacity to resist disease), or new functions (e.g., terminator seeds that grow sterile plants).
Although the educational uses of these statistical methods are of unproven value, they are being deployed for re-engineering education along similar lines, from teacher education programs and recruitment strategies, to dismissing teachers who resist a regime of education preoccupied with measures of cost-effectiveness, cost-efficiency, and such.
Of course, the technologies of genetic engineering also have unintended consequences. Among major risks are: disturbing a thriving ecological system, doing harm to strengths in existing species, unexpected and toxic reactions to changes introduced into reproductive systems, and the development of resistance to engineered interventions. Other concerns bear on unhealthy concentrations of traits by inbreeding, and the irreversibility of these processes. Although consequences such as these do have counterparts in education, too little attention is being given to them.
The early twentieth century “cult of efficiency” that developed around the machinations of mechanical engineer Frederick W. Taylor has returned; now under the auspices of William L. Sanders, who has promoted his use of statistical methods suitable for genetic engineering in agriculture to educators and policy-makers. Others have assisted in this marketing campaign, but without addressing the implications of making value-added measures a centerpiece of federal policy and treating teachers as no different from corn plants or sows, and students as if they are the proxies for test scores.
Rather than dwelling on marginal differences in models and calculations, I think far more attention should be given to genetic engineering as a source of methods for judging effective teachers and as the underlying metaphor for current efforts to improve educational outcomes.
The origin of these statistical measurement methods considerably predates genetic engineering, and can count many successes as well as failures. I’d hate to give up GPS and return to an era of seat-of-the-pants medicine, with homunculi and spontaneous generation, for example.
However, your point about unintended consequences still stands. The problem is not the measurement methods per se, but misapplication. If you don’t understand how the thing you measure (test scores) relates to the thing you want (learning) systemically, it’s highly likely that there will be perverse side effects.
Personally, as a small-scale, part-time educator of home-schooled kids, I find it inconceivable that one-size-fits-all test scores are a good metric or goal for kids who are, in all likelihood, diverse in talent and developing at wildly different rates. Testing is useful information, but shouldn’t be the central pillar of education.
It seems to me that much of the obsession with testing and Darwinian selection of teachers is dodging the fundamental problem, that doing the job better in aggregate will take more resources than we now devote to education.
@John – I quite agree. The common problem of the two approaches is that there’s little understanding of how either test scores or human ratings correlate with the actual underlying learning that we’re seeking.
There was a pretty convincing paper demonstrating that value added scores (generated by a slightly different model than the one NYC used) of elementary school teachers were positively correlated with desirable life outcomes for their students (graduating high school, going to college, not getting pregnant too early, etc.) after controlling for the usual suspect potential confounding variables. Here’s the link: http://obs.rc.fas.harvard.edu/chetty/value_added.pdf
Interesting. Thanks for the link. There’s a lot to this. A couple quick observations:
Their estimate of the effect of noise on measurement seems to imply a clearer signal than I see in the NY data.
They cite a novel policy-resistance effect: their positive results about VAM are contingent on not using it for evaluation. When it’s used for evaluation, pathologies like cheating emerge that may distort the signal. (Alarmingly, they have to clip out the top 2% of teachers for suspected cheating.)
Their persistence effect (that teacher effects fall to about 1/3 of their original value, then remain at that level) has an interesting implication for tracking: students unlucky enough to have a few bad teachers could end up in lower course tracks. This would serve to amplify the single-teacher effects (i.e., it’s a positive loop – success to the successful – applied to noisy initial conditions).