Tag: endogenous

Closing loops – practicalities

Hybrid models are the solution to blending endogenous elegance with practicality.

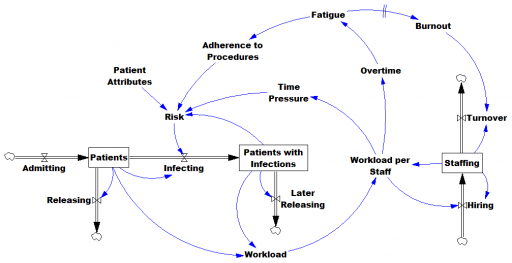
My last post probably sounds like I disagree with Jack Homer’s recommendation to tolerate some exogenous drivers and consideration of policy feasibility. Actually I don’t. In fact, we at Ventana probably do more data-intensive SD than anyone. I build hybrid models all the time.

When philosophizing about the best way to change the world, it’s easy to lose sight of some practical considerations that influence choices:

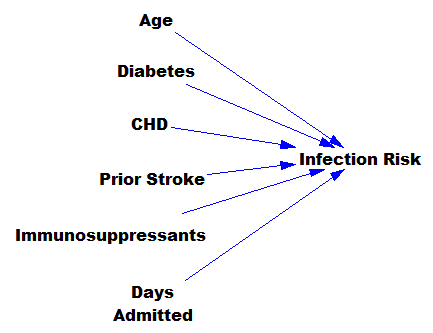
  • Cost. It’s expensive to develop an elegant, endogenous theory for things like interest rates that you might normally think of as exogenous to a firm. On the other hand, it’s also expensive to collect and use data – often 1/3 of project cost in our experience.
  • Clarity. Exogenous variables complicate the analysis of a model, because you have driven behavior on top of the model’s endogenous dynamics. I think this makes it harder to understand the basic behavior, because you lose the insight you might gain from starting a model in equilibrium and perturbing it with policies.
  • Calibration. On the other hand, using exogenous drivers increases your ability to gain insight from comparison of model behavior to data. This is not a definitive test, but you can definitely use it to estimate uncertain parameters and weed out certain dumb ideas.
  • Client. You have to meet people where they are. If, historically, they think R^2 is the definitive measure of success, you’d better deliver. You can explain why that’s a bad metric and present a more endogenous view of the situation later, after you’ve established trust.

I think there’s no clear answer – the extent to which endogenous or exogenous elements are preferred has to be a situation-specific decision. In my own work, I often use a two-pronged approach, and two ways to structure that have emerged:

  • Build a single, large, calibrated model with some exogenous drivers. Build endogenous submodels or metamodels for equilibrium experiments and to  explain key features of the big model.
  • Build a single, elegant endogenous model, with few drivers. Use smaller exogenous models, or statistical and machine learning tools, to understand local features of the data, incorporating those insights into the endogenous model without using the data directly.

Prediction, in context

I’m increasingly running into machine learning approaches to prediction in health care. A common application is identification of risks for (expensive) infections or readmission. The basic idea is to treat patients like a function approximation problem.

The hospital compiles a big dataset on patient demographics, health status, exposure to procedures, and infection outcomes. A vendor slurps this up and turns some algorithm loose on the data, seeking the risk factors associated with the infection. It might look like this:

… except that there might be 200 predictors, not six – more than you can handle by eyeballing scatter plots or control charts. Once you have a risk model, you know which patients to target for mitigation, and maybe also which associated factors to pursue further.

However, this is only half the battle. Systems thinkers will recognize this model as a dead buffalo: a laundry list with unidirectional causality. The real situation is rich in feedback, including a lot of things that probably don’t get measured, and therefore don’t end up in the data for consideration by the algorithm. For example:

Infections aren’t just a random event for the patient; they happen for reasons that are larger than the patient. Even worse, there are positive feedbacks that can make prevention of infections, and errors more generally, hard to manage. For example, as the number of patients with infections rises, workload goes up, which creates time pressure and fatigue. That induces shortcuts and errors that create risk for patients, leading to more infections. Infections spread to other patients. Fatigued staff burn out and turn over faster, which dilutes the staff experience that might otherwise mitigate risk. (Experience, like many other dynamics, is not shown above.)

An algorithm that predicts risk in this context is certainly useful, because anything that reduces risk helps to diminish the gain of the vicious cycles. But it’s no longer so clear what to do with the patient assessments. Time spent on staff education and action for risk mitigation has to come from somewhere, and therefore might have unintended consequences that aren’t assessed by the algorithm. The algorithm is actually blind in two ways: it can’t respond to any input (like staff fatigue or skill) that isn’t in the data, and it probably  isn’t statistically smart enough to deal with the separation of cause and effect in time and space that arises in a feedback system.

Deep learning systems like Alpha Go Zero might learn to deal with dynamics. But so far, high performance requires very large numbers of exemplars for reinforcement learning, and that’s never going to happen in a community hospital dataset. Then again, we humans aren’t too good at managing dynamic complexity either. But until the machines take over, we can build dynamic models to sort these problems out. By taking an endogenous point of view, we can put machine learning in context, refine our understanding of leverage points, and redesign systems for greater performance.