Bernoulli asks, “how long have we been here?” Poisson replies, “I have no idea.”
Bad joke aside, memoryless behavior is a key component of a toy model of car rentals I made a while ago. I recently noticed that I was a bit lazy in my choice of RANDOM functions, so I’ve produced an update.
The difference is in the use of Poisson and Binomial distribution functions. In the original, I used the Poisson distribution everywhere to represent arrival processes. That’s reasonable in the limit, where a large number of candidate arrivals are realized with a small probability, such that the expected arrivals occur at some finite rate.
Think of a lemonade stand on a busy street – there’s a very large population of potential lemonade buyers, but only a small fraction actually stop for a drink. Normally, we don’t want to model the street and the traffic generation process, so it’s reasonable to assume independent arrivals from a large pool at some rate that we can measure, using the Poisson distribution. This is similar to using a cloud in SD to indicate a source or sink that we aren’t modeling.
In the car rental model, the arrival of customers is a good example of this. But other processes in the model are not. Consider the servicing of returned vehicles:
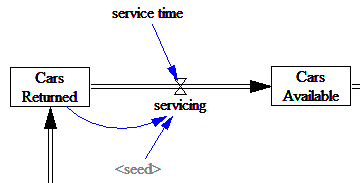
Here, the company is not servicing all vehicles in the universe at a finite rate, but instead they’re servicing a known queue (the stock of cars returned) with some expected time for each. If servicing time is exponentially distributed (the equivalent of the continuous stock draining process), the probability of any individual car getting serviced in the next time step is inversely proportional to the service time. So, this is a Binomial distribution, i.e. a series of Bernoulli trials with n=cars returned and p=TIME STEP/service time.
Does the difference matter? Normally, not much. As long as the arrival rate is a smallish fraction of the stock of potential arrivals, the Poisson distribution will be a close approximation of the Binomial. But the Poisson distribution fails a key reality check: it can generate an arbitrarily large number of arrivals at any time. The probability of this occurring becomes significant if the service time is short with respect to TIME STEP. The Binomial distribution, on the other hand, is properly bounded above by the number of candidate arrivals (Cars Returned).
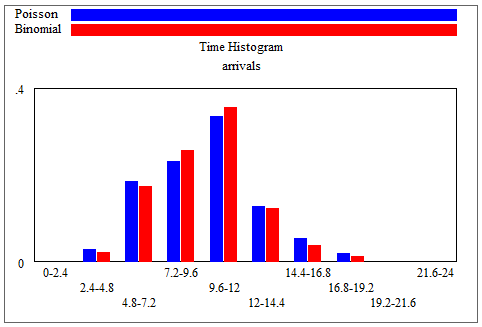
Here’s an example. With Binomial n = 100 and p = 1/10, or equivalently Poisson arrivals of 10 per time, the distributions are practically identical:
But with n = 10 and p = 1/2 (i.e. service time = 2*TIME STEP), the similar Poisson distribution with arrivals = 5 per time yields rare instances with 11, 12 or 13 out of 10 cars arriving in this sample of 1000 times:
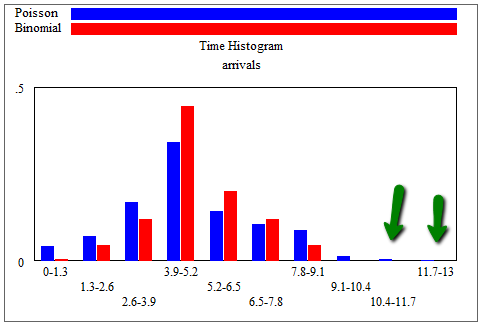
That’s not good!
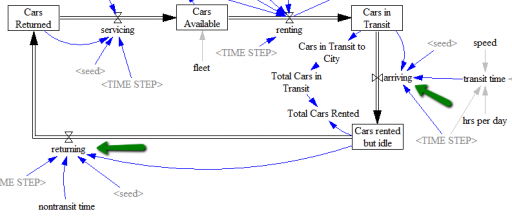
There’s another limitation of my toy model that I haven’t addressed. The Binomial arrivals are memoryless for individual cars in the service or intercity arrival queues. That assumes that the probability that a car arrives in the next moment is independent of its residence time in the queue. That’s fine for exponential decay, but for real world processes it’s usually not quite right. There’s a certain minimum time required to service a car or drive from city A to city B.
The solution is to decompose the process into multiple steps. This is essentially the same thought process as choosing a delay order. For servicing, for example, you could represent the minimum time needed to clean and fuel a car as a pipeline delay, then add randomness to describe additional delays that occur as employees take breaks, equipment fails, etc. Similarly, for the delay between rental and return, you could modify the existing structure to treat arriving as a discrete delay (representing the time required to get from A to B), plus an additional random delay before returning, representing variation from traffic congestion and sightseeing.
See also:
This is a pretty typical example of doing discrete event simulation in Vensim. Vensim is really targeted at continuous time and values, but with minimal extra work it can handle a lot of discrete cases. There’s a video covering the basics at vensim.com.
