So far, I’ve established that the qualitative results of Rahmstorf (R) and Grinsted (G) can be reproduced. Exact replication has been elusive, but the list of loose ends (unresolved differences in data and so forth) is long enough that I’m not concerned that R and G made fatal errors. However, I haven’t made much progress against the other items on my original list of questions:
- Is the Grinsted et al. argument from first principles, that the current sea level response is dominated by short time constants, reasonable?
- Is Rahmstorf right to assert that Grinsted et al.’s determination of the sea level rise time constant is shaky?
- What happens if you impose the long-horizon paleo constraint to equilibrium sea level rise in Rahmstorf’s RC figure on the Grinsted et al. model?
At this point I’ll reveal my working hypotheses (untested so far):
- I agree with G that there are good reasons to think that the sea level response occurs over multiple time scales, and therefore that one could make a good argument for a substantial short-time-constant component in the current transient.
- I agree with R that the estimation of long time constants from comparatively short data series is almost certainly shaky.
- I suspect that R’s paleo constraint could be imposed without a significant degradation of the model fit (an apparent contradiction of G’s results).
- In the end, I doubt the data will resolve the argument, and we’ll be left with the conclusion that R and G agree on: that the IPCC WGI sea level rise projection is an underestimate.
I’ll elaborate on the 3rd point. Consider G’s Moberg fit. The estimate identifies a short time constant (208 years), and a small value for a (1.29 meters/C). R objects that the slope (given by a) is far less than the long-term slope one would expect from paleo constraints (roughly 20 meters/C). At the same time, G’s combination of parameters yields a high sensitivity (a/tau) of 6.3 mm/yr/C vs. R’s 3.4 mm/yr/C. From G’s figure 5, it appears that the data tightly constrain the value of a (top row, second panel):
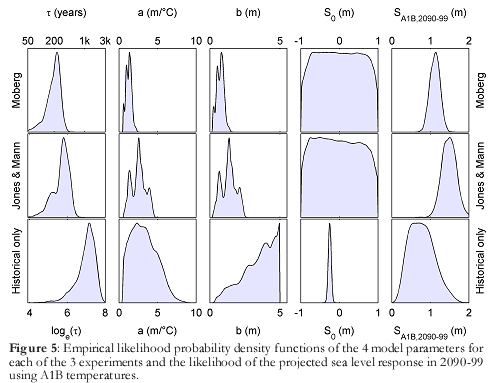
I suspect that this is an artifact of the presentation. I’ll bet that the payoff surface with respect to a and tau is an off-axis ellipse, like the following: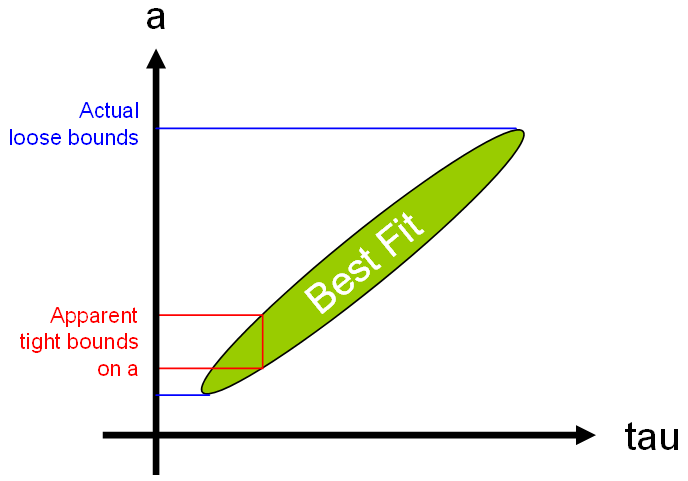
The region of a and tau yielding the best fit to data is elliptical, because the ratio a/tau largely determines the transient response (as we showed in the first installment). A wide variety of values of a might fit the data reasonably well, as long as a corresponding tau (within the green region) is chosen. Moving away from the ellipse along its minor axis, on the other hand, corresponds to a change in a/tau, which quickly diminishes the fit. My guess is that G’s figure 5 represents the red transect through the ellipse – that is, an experiment with a while holding tau constant. That yields a narrow confidence interval, because it changes a/tau. However, that confidence bound is an underestimate of the true multivariate bounds on a (blue).
To get the right answer, you have to explore the whole hypervolume (remembering that we’re actually working in 4 dimensions, not 2). Assuming good behavior, one might get away with local exploration around the best fit, to find the principle axes of the ellipse. Either way, it’s a bit of a pain (and will be for me too – Vensim’s default payoff sensitivity evaluation calculates the red bounds, not the blue, and thus is not immediately helpful).
I haven’t actually run this experiment yet, so next installment we’ll find out if I’m right. To do that, I’ll first set up the model to run with Kalman Filtering, in order to get a better picture of the payoff surface.

Tom —
Great work digging into this area. Should help clear up some of the confusion we run into out there as we talk about sea level rise scenarios.
D