Sloppy System Dynamics

This post should be required reading for all modelers. And no, I’m not going to reproach sloppy modeling practices. This is much more interesting than that.

Sloppy models are an idea that formalizes a statement Jay Forrester made long ago, in Industrial Dynamics (13.5):

The third and least important aspect of a model to be considered in judging its validity concerns the values for its parameters (constant coefficients). The system dynamics will be found to be relatively insensitive to many of them. They may be chosen anywhere within a plausible range. The few sensitive parameters will be identified by model tests, and it is not so important to know their past values as it is to control their future values in a system redesign.

This remains true when you’re interested in estimation of parameters from data. At Ventana, we rely on the fact that structure and parameters for which you have no measurements will typically reveal themselves in the dynamics, if they’re dynamically important. (There are always pathological cases, where a nonlinearity makes something irrelevant in the past important in the future, but that’s why we don’t base models solely on formal data.)

Now, the required part. 

James Sethna and colleagues at Cornell have formalized Forrester’s observation, and call the insensitivity phenomenon “sloppiness.” What follows is a brief summary, but I encourage you to follow the links to the originals.

What is sloppiness?

It’s long been known that many multiparameter models are loosely constrained, or ill conditioned: many parameter sets can exhibit the same behavior. When we were exploring some problems in systems biology, though, we were startled by the giant ranges of parameters that could still fit the data. Each of the parameters in our model could vary by at least a factor of fifty, and many by factors of thousands (left) without changing the behavior. And yet, the model was useful – these widely varying parameters sets agreed for many important predictions.

Calling a model like this “loosely constrained” is like calling the ocean wet. We call these sloppy models. We emphasize, though, that one should think of sloppiness not as a failure of the model! Some of the most precise calculations in physics (variational wavefunctions used in quantum Monte Carlo for high-accuracy molecular energy calculations) are sloppy. We shall see that sloppiness is often compatible with good predictive power, for most everything of interest except the parameters.

What are sloppy models?

What are Sloppy Models? We claim that many if not most models with several fitting parameters (say, more than five) are sloppy. Sloppy models are called ‘poorly constrained’ and ‘ill-conditioned’ because it is difficult to use experimental data to figure out what their parameters are. …

Is sloppiness special to biological systems? Apparently not! We’ve found sloppiness in multiparameter models spanning many fields, from models of insect flight, to interatomic potentials, to accelerator design – every multiparameter model that we have studied so far appears to be sloppy.

This resonates with my own experience with many different kinds of models, including climate, supply chains, traffic, projects and pharmaceuticals marketing.

As they show with some examples, sloppiness arises from the shape of the cost function, i.e. the payoff function that measures fit to data as a function of parameters.

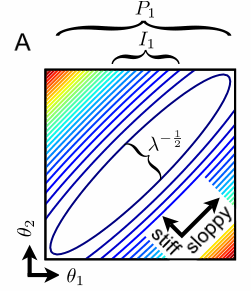
Near enough to the best fit, we almost always will find that the cost contour surfaces form ellipsoids – stretched long along sloppy directions, and pinched in along the stiff directions. These ellipsoids can be described by the eigenvalues and eigenvectors of the Hessian … of the cost near the best fit. The eigenvectors point along the different axes of the ellipse; we call these parameter combinations eigenparameters, as opposed to the bare parameters that we originally chose to write our model in terms of. …

Some directions in the parameter space are stiff, causing large changes in the goodness of fit metric, while others are sloppy, causing small changes. Along sloppy directions, you can’t use the data to measure the parameters, because different combinations yield behavior that is practically indistinguishable. However, the insensitivity of the behavior to these parameter combinations also means that (policy) predictions are robust to their uncertainty.

Why is science possible?

So, physics, systems biology, and presumably much of the rest of science all rely on a kind of information compression about the system rules. The collective system behavior in each case relies on only a few ‘stiff’ combinations of parameters from the many variables in the full microscopic description. In physics, we have systematic methods for extracting these emergent, collective theories from the microscopic complexity. In other fields, we don’t have such tools — but the theories show the same kind of independence from the microscopic details

Climate provides one example of this. In the Schneider Thompson model (and other energy balance models), three parameters are strongly entangled: climate sensitivity, ocean heat transfer, and the magnitude of historic aerosol forcing. You can get similar global temperature trajectories with high sensitivity and fast heat transfer, or low sensitivity and slow heat transfer. This is a sloppy direction. On the other hand, you can quickly rule out combinations in the stiff perpendicular direction, like high sensitivity with slow heat transfer, because they produce implausible temperatures. If you’re interested in temperature, and not the parameter values per se, then the sloppiness doesn’t matter much. You get similar future transient temperature responses for this century with any combination of parameters that produces plausible historic temperatures.

Aerosols are entangled the same way – high historic aerosols imply that some warming has been suppressed, and therefore that the sensitivity-transfer combination must also be larger. But this is a little trickier, because we may vary aerosols independently from greenhouse gases in the future, so we have some intrinsic interest in their behavior. Temperature measurements can’t help us with this; we need other kinds of models and data to tackle the aerosol dimension independently. Failing that, we need to account for the uncertainty in predictions.

Do parameters matter?

One can of course design special experiments to measure one parameter at a time (avoiding the collective behavior of the model as a whole). If we did measure all of the parameters …, and the model still fit the data, then we could be far more confident that the model was really correct – that there were no important missing links or reaction pathways, that were fit by fiddling (or renormalizing) the existing model parameters.

…

Is measuring parameters useful? In particular, suppose (as is usually the case) it is not feasible to measure every last parameter. Can one extract predictions from models when only half of the parameters are measured? How about all but one parameter? Indeed, for sloppy models, one might expect that even one missed parameter could make for drastic problems.

…

Our conclusion? Sloppy systems have a weird connection between parameters and model behavior. Not only can’t you use the behavior of the model to determine the parameters, but conversely a partial knowledge of the parameters is useless at making predictions about model behavior. The biologists are right: measuring parameters is boring, if your system is sloppy.

Sethna et al. go on to explore the differential geometry of the problem and a variety of applications. They also suggest a protocol for experimental design in sloppy systems.

I think there’s much to be gained by cross-fertilization of thinking here.