Coronavirus Curve-fitting OverConfidence

This is a follow-on to The Normal distribution is a bad COVID19 model.

I understand that the IHME model is now more or less the official tool of the Federal Government. Normally I’m happy to see models guiding policy. It’s better than the alternative: would you fly in a plane designed by lawyers? (Apparently we have been.)

However, there’s nothing magic about a model. Using flawed methods, bad data, the wrong boundary, etc. can make the results GIGO. When a bad model blows up, the consequences can be just as harmful as any other bad reasoning. In addition, the metaphorical shrapnel hits the rest of us modelers. Currently, I’m hiding in my foxhole.

On top of the issues I mentioned previously, I think there are two more problems with the IHME model:

First, they fit the Normal distribution to cumulative cases, rather than incremental cases. Even in a parallel universe where the nonphysical curve fit was optimal, this would lead to understatement of the uncertainty in the projections.

Second, because the model has no operational mapping of real-world concepts to equation structure, you have no hooks to use to inject policy changes and the uncertainty associated with them. You have to construct some kind of arbitrary index and translate that to changes in the size and timing of the peak in an unprincipled way. This defeats the purpose of having a model.

For example, from the methods paper:

A covariate of days with expected exponential growth in the cumulative death rate was created using information on the number of days after the death rate exceeded 0.31 per million to the day when different social distancing measures were mandated by local and national government: school closures, non-essential business closures including bars and restaurants, stay-at-home recommendations, and travel restrictions including public transport closures. Days with 1 measure were counted as 0.67 equivalents, days with 2 measures as 0.334 equivalents and with 3 or 4 measures as 0.

This postulates a relationship that has only the most notional grounding. There’s no concept of compliance, nor any sense of the effect of stringency and exceptions.

In the real world, there’s also no linear relationship between “# policies implemented” and “days of exponential growth.” In fact, I would expect this to be extremely nonlinear, with a threshold effect. Either your policies reduce R0 below 1 and the epidemic peaks and shrinks, or they don’t, and it continues to grow at some positive rate until a large part of the population is infected. I don’t think this structure captures that reality at all.

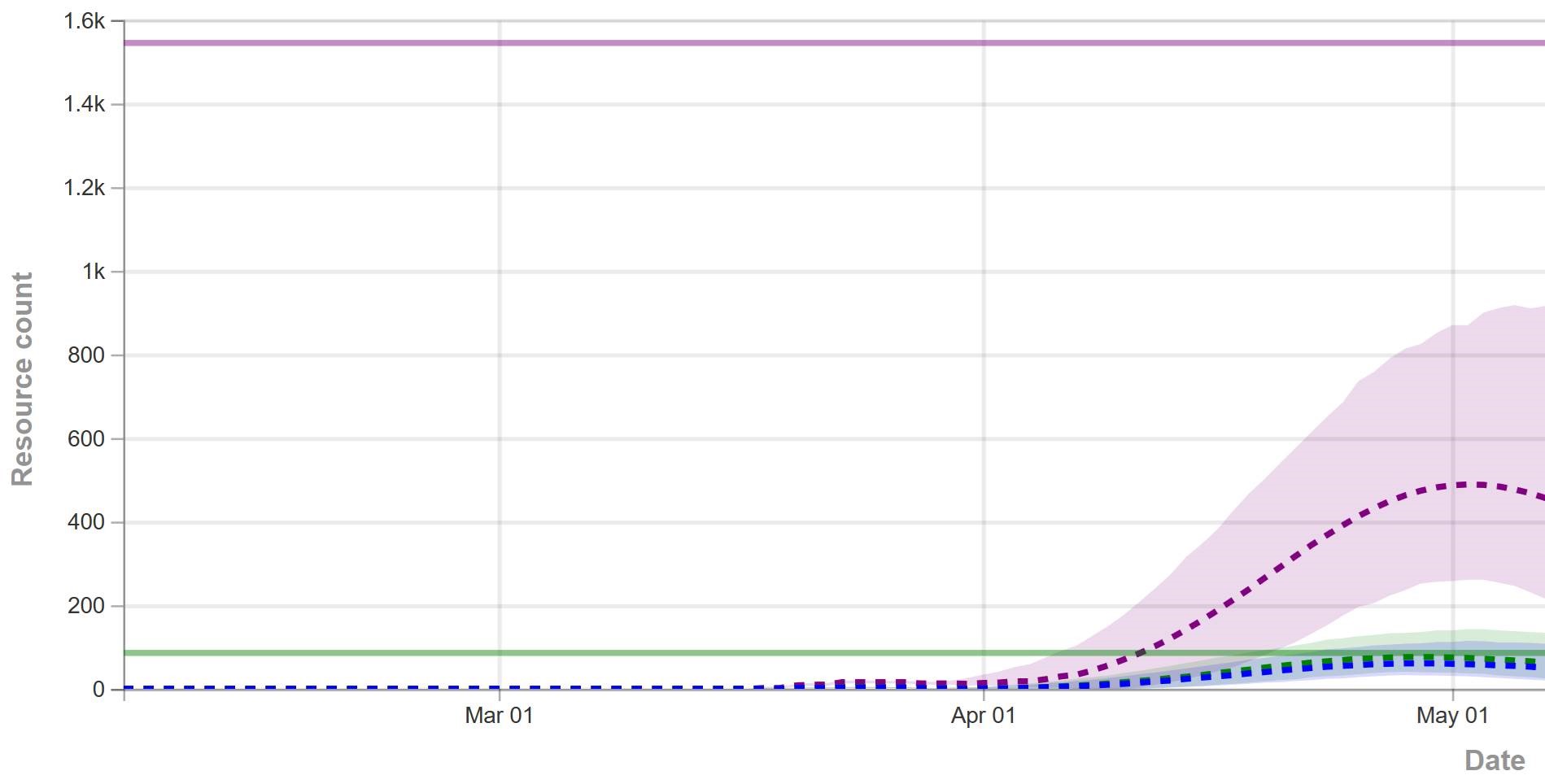
That’s why, in the IHME figure above (retrieved yesterday), you don’t see any scenarios in which the epidemic fizzles, because we get lucky and warm weather slows the virus, or there are many more mild cases than we thought. You also don’t see any runaway scenarios in which measures fail to bring R0 below 1, resulting in sustained growth. Nor is there any possibility of ending measures too soon, resulting in an echo.

For comparison, I ran some sensitivity runs my model for North Dakota last night. I included uncertainty from fit to data (for example, R0 constrained to fit observations via MCMC) and some a priori uncertainty about effectiveness and duration of measures, and from the literature about fatality rates, seasonality, and unobserved asymptomatics.

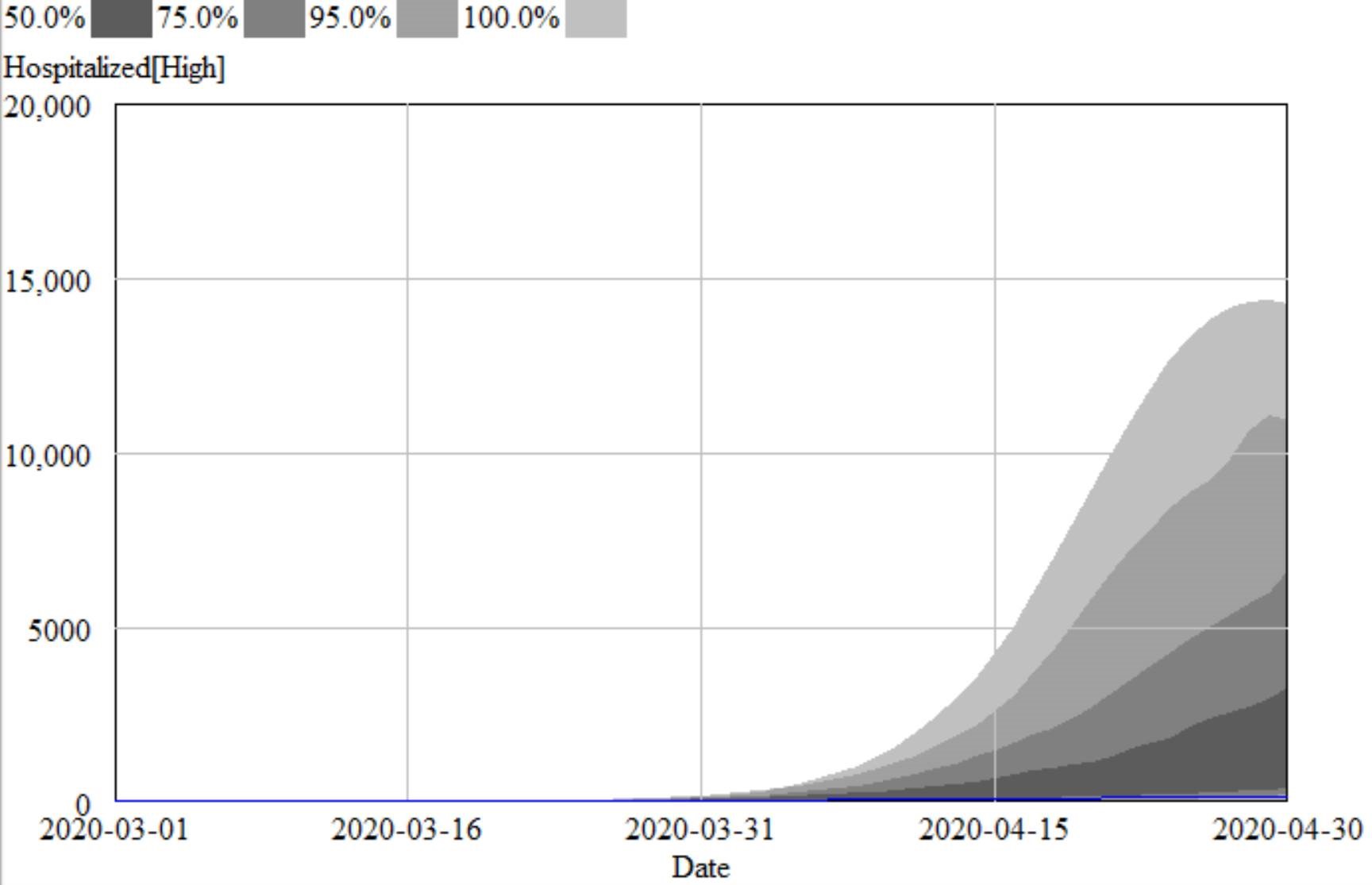
I found that I couldn’t exclude the IHME projections from my confidence bounds, so they’re not completely crazy. However, they understate the uncertainty in the situation by a huge margin. They forecast the peak at a fairly definite time, plus or minus a factor of two. With my hybrid-SEIR model, the 95% bounds include variation by a factor of 10. The difference is that their bounds are derived only from curve fitting, and therefore omit a vast amount of structural uncertainty that is represented in my model.

Who is right? We could argue, but since the IHME model is statistically flawed and doesn’t include any direct effect of uncertainty in R0, prevalence of unobserved mild cases, temperature sensitivity of the virus, effectiveness of measures, compliance, travel, etc., I would not put any money on the future remaining within their confidence bounds.