Failure to account for bathtub dynamics is a basic misperception of system structure, that occurs even in simple systems that lack feedback. Research shows that pattern matching, a common heuristic, leads even highly educated people to draw incorrect conclusions about systems as simple as the entry and exit of people in a store.
This can occur in any stock-flow system, which means that it’s ubiquitous. Here’s the basic setup:
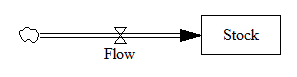Replace “Flow” and “Stock” with your favorite concepts – income and bank balance, sales rate and installed base, births and rabbits, etc. Obviously the flow causes the stock – by definition, the flow rate is the rate of change of the stock level. There is no feedback here; just pure integration, i.e. the stock accumulates the flow.
The pattern matching heuristic attempts to detect causality, or make predictions about the future, by matching the temporal patterns of cause and effect. So, naively, a pattern matcher expects to see a step in the stock in response to a step in the flow. But that’s not what happens:
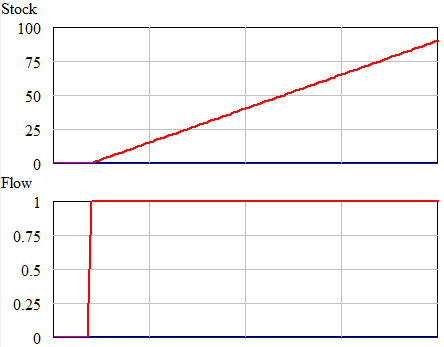Pattern matching fails because we shouldn’t expect the patterns to match through an integration. Above, the integral of the step ( flow = constant ) is a ramp ( stock = constant * time ). Other patterns are possible. For example, a monotonically decreasing cause (flow) can yield an increasing effect (stock), or even nonmonotonic behavior if it crosses zero:
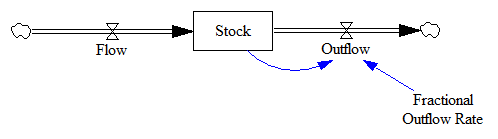
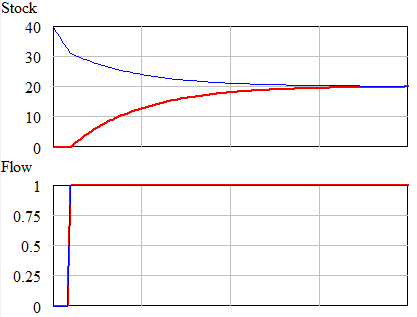
If you add simple outflow feedback, there are even more possibilities. Here, we have our flow and stock, with an additional outflow that is a fraction of the stock per unit time:
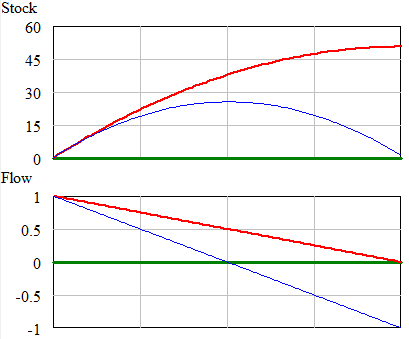
In this case, with the same step up Flow pattern the stock can go up or down, depending on whether its initial level is such that the outflow exceeds the inflow, or not:
To ensure that the universe is as confusing as possible, there are some cases where pattern matching seems to work. For example, in steady state growth, where a flow grows exponentially at a constant rate, its associated stock will grow exponentially at the same rate (because the integral of e^x is e^x). Similarly, the integral of a ramp (c*time) is a parabola (c/2*time^2), which is approximately linear (i.e. resembling a ramp) over short time horizons. So, it’s not uncommon to see vehicle sales (flow) and fleet (stock) plotted together appear to have the same trend (especially with nonzero scales on the axes), or to see a consistent relationship between deficits (flow) and debts (stock). Pattern matching also works when a stock has time to come into equilibrium with the flows driving it. If the time horizon over which one observes the behavior is long with respect to the time constant of the stock’s dynamics, one sees the equilibrium relationship, stock = f(flow), relatively unobscured by integration.
My favorite example of bathtub misperceptions comes from Erling Moxnes work with renewable resource problems. In experiments with managing simulated reindeer herds, dependent on stocks of lichen for grazing, many participants adopt an inappropriately static mental model – that is, they ignore the dynamics of accumulation. They start with a reindeer herd that is too large, so that the flow of grazing depletes the stock of lichen. Taking corrective action, they reduce the reindeer herd, but not enough, so that the lichen stock continues to decline. At this point, they have some data: grazing has gone down, and lichen has gone down. Some question the static model and course-correct in the right direction (but not fast enough), but a subset of participants instead take pattern matching to its absurd logical end. They conclude that if grazing down->lichen down works, it follows that the way to increase lichen is to increase grazing. You can imagine how that works out.
Next up: the extension of all this to naive statistical comparisons.
Nice post–illuminating, and not overly complicated.
Thanks – that’s what I was shooting for.
Whenever I open up my worn copy of “Business Dynamics” by John Sterman (2000), I cringe looking at p. 194, where Sterman shows “four equivalent representations” of (a) stock and flow structure (consisting of just an inflow and an outflow from and into clouds without any other flows), which explicitly shows the bathtub (hydraulic) metaphor. There he even writes “The bathtub and stock and flow diagrams may appear to be less rigorous than the integral of differential equation representations, but they are precisely (sic!) equivalent and contain exactly (sic!) the same information.”
Maybe my understanding of “precisely” and “exactly” are off but for one, the differential equation is not given as a couplet of an algebraic initial equation (e.g., Stock(t0) = Initial Value of Stock) plus a differential equation, and the statement is thus already off, since the integral equation given has an explicit Stock(t0). [Just as a side node: I fail to see any place where Sterman talks about the true nature of a state “variable”, which is that of a “function”—that evil thing is never mentioned, is it?]
Moving on to compare the SFD with the “Hydraulic Metaphor” (e.g., the bathtub being filled and drained by two pipes with valves) we note that the SFD has also no notation of an initial amount of substance contained in the stock. But the arguably greatest mistake in my opinion is that the whole field is not able to move away from a very false physical analogy, which confuses people, who have not flunked physics in school.
1. The bathtub is shown with some current amount of water in it, so it does maybe not include the initial value information as claimed? (If the “snapshot” was taken at t = t0, then we should not be able to see any water flowing …)
2. Stocks can in general become negative—a bathtub cannot contain anti-matter and thus the precise equivalence is violated again.
3. Since we can see water flowing (at least in Sterman’s bathtub picture), we can deduce the current rates of in- and outflow, which is not possible in equations and SFD given on p. 194. [Interestingly, the example also makes the “snapshot” test less convincing imho.]
4. SFDs use the valve symbol (probably from control- and process engineering), which seems to come from Forrester’s “decision function” notion. But
a) Flows in social and other sciences need not be governed by “decisions” nor need they be subject to “control” in a stricter sense. They are just explanatory processes (“mechanisms”) that tell us how states (=attributes of systems) change, which may sometimes be controlled.
b) Valves pretty much exclusively control a flow that is not “caused” by them, e.g., by opening or closing the faucet to fill the bathtub, we can set the flow to any value between 0 and MAX_RATE OF FLOW, which is determined by the utility company (that information link is missing). The valve for the outflow can also only limit (never extend) the rate of flow determined by the hydro-static potential in the bathtub (stored energy) and the implicit link from Stock to Outflow is omitted in the SFD representation.
c) Valves can typically not reverse flows, but exactly that is the general notion of a rate, which might become negative (Sterman continues using a unidirectional flow indicator even when the rate is a net rate that may become negative). [Unidirectional flows introduce conditionality with regard to feedback loops, do they not?]
Thus, the hydraulic metaphor not only “appears less rigorous”—it most definitely is and should at least be corrected to one that shows two pumps operating on the bathtub. Also, bathtubs in general are finite reservoirs that cannot hold negative content, which is “precisely and exactly” not the case for state variables in general and those given in the equations on p. 194 of the “System Dynamics Bible.”
In addition to the nonnegativity issue, bathtubs also have an upper limit, where the dynamics change when water runs over the rim.
Yet another limitation to the bathtub analogy is the outflow nonlinearity pointed out by the Bergen crew:
https://metasd.com/2011/08/limits-to-bathtubs/
Thanks, that’s indeed Torricelli’s law governing the outflow from a bathtub.
But I would stress that to me the greatest problems arise the from “valve” analogy, which really is a “check valve” analogy as flows are typically shown as unidirectional, even when they in general are bidirectional (Sterman pretty much always shows a net rate as a unidirectional flow as if we could transport anti-matter). Valves are limiters not activating processes and most people do not associate flow reversal with a valve.
But maybe we will see an update in the 2030 edition of Business Dynamics? Maybe the field is dynamic and open to change? 🙂