My Delay Sandbox model illustrates the correspondence between Nth-order delays and the Erlang distribution (among other things).
This model provides some similar insights – this time in Ventity. It’s a hybrid of classic continuous SD and agent equivalents.
First, the Erlang3 entitytype compares the classic 3rd-order aging chain’s behavior to analytical equivalents, as in the Delay Sandbox. The analytic values are computed in a set of Ventity’s new macros:
Notice that the variances, which arise from Euler integration with a finite time step, are small enough to be uninteresting.
Second, the model compares the dynamics of discrete agent populations to the analytic Erlang results. To do this, the Model entity creates populations of agents at time 0, and (for comparison) computes the expected surviving population according to the Erlang distribution:
The agents live for a time, then self-delete according to two different strategies:
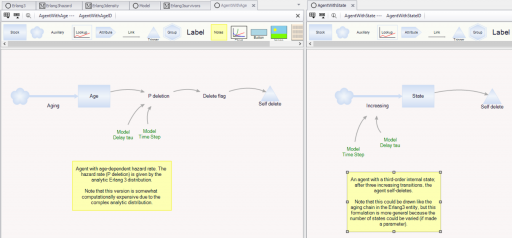
On the left, an agent tracks its own age, and has an age-specific probability of mortality (again, thanks to the hazard rate of the Erlang distribution). On the right, an agent has a state counter, and mortality occurs when the number of state transitions reaches 3.
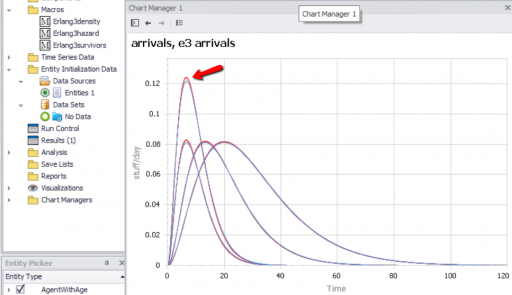
We can then compare the surviving agent populations (blue) to the Erlang expectation (red):
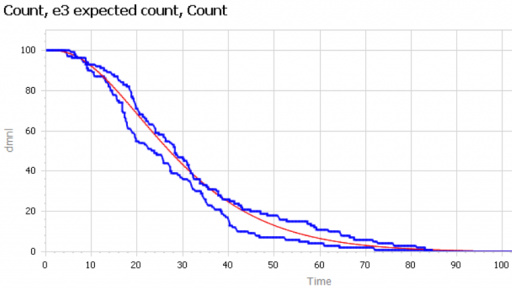
When the population is small (above, 100), there’s some stochastic variation around the expected result. But for larger populations, the difference is negligible.
The model: Erlang3 4 (2).zip
