Month: February 2009

Sea Level Rise Models – III

Starting from the Rahmstorf (R) parameterization (tested, but not exhaustively), let’s turn to Grinsted et al (G).

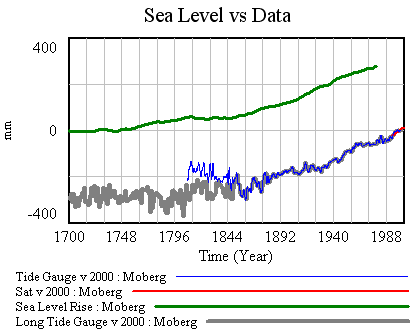
First, I’ve made a few changes to the model and supporting spreadsheet. The previous version ran with a small time step, because some of the tide data was monthly (or less). That wasted clock cycles and complicated computation of residual autocorrelations and the like. In this version, I binned the data into an annual window and shifted the time axes so that the model will use the appropriate end-of-year points (when Vensim has data with a finer time step than the model, it grabs the data point nearest each time step for comparison with model variables). I also retuned the mean adjustments to the sea level series. I didn’t change the temperature series, but made it easier to use pure-Moberg (as G did). Those changes necessitate a slight change to the R calibration, so I changed the default parameters to reflect that.

Now it should be possible to plug in G parameters, from Table 1 in the paper. First, using Moberg: a = 1290 (note that G uses meters while I’m using mm), tau = 208, b = 770 (corresponding with T0=-0.59), initial sea level = -2. The final time for the simulation is set to 1979, and only Moberg temperature data are used. The setup for this is in change files, GrinstedMoberg.cin and MobergOnly.cin.

Moberg, Grinsted parameters

Continue reading “Sea Level Rise Models – III”

Sea Level Rise Models – II

Picking up where I left off, with model and data assembled, the next step is to calibrate, to see whether the Rahmstorf (R) and Grinsted (G) results can be replicated. I’ll do that the easy way, and the right way.

An easy first step is to try the R approach, assuming that the time constant tau is long and that the rate of sea level rise is proportional to temperature (or the delta against some preindustrial equilibrium).

Rahmstorf estimated the temperature-sea level rise relationship by regressing a smoothed rate of sea level rise against temperature, and found a slope of 3.4 mm/yr/C.

Rahmstorf figure 2

Continue reading “Sea Level Rise Models – II”

Sea Level Rise Models – I

A recent post by Stefan Rahmstorf at RealClimate discusses a new paper on sea level projections by Grinsted, Moore and Jevrejeva. This paper comes at an interesting time, because we’ve just been discussing sea level projections in the context of our ongoing science review of the C-ROADS model. In C-ROADS, we used Rahmstorf’s earlier semi-empirical model, which yields higher sea level rise than AR4 WG1 (the latter leaves out ice sheet dynamics). To get a better handle on the two papers, I compared a replication of the Rahmstorf model (from John Sterman, implemented in C-ROADS) with an extension to capture Grinsted et al. This post (in a few parts) serves as both an assessment of the models and a bit of a tutorial on data analysis with Vensim.

My primary goal here is to develop an opinion on four questions:

  • Can the conclusions be rejected, given the data?
  • Is the Grinsted et al. argument from first principles, that the current sea level response is dominated by short time constants, reasonable?
  • Is Rahmstorf right to assert that Grinsted et al.’s determination of the sea level rise time constant is shaky?
  • What happens if you impose the long-horizon paleo constraint to equilibrium sea level rise in Rahmstorf’s RC figure on the Grinsted et al. model?

Paleo constraints on equilibrium sea level

Continue reading “Sea Level Rise Models – I”