For many aspects of models, we have well-accepted rules that define good practice. All physical stocks must have first-order negative feedback on the outflow. Normalize your lookup tables. Thou shalt balance units.
In some areas, the rules haven’t been written down. Subscripts (arrays) are the poor stepchild of dynamic models. They simply didn’t exist when simulation languages emerged, and no one really thinks about them much. They’re treated as a utility, like memory allocation in C, rather than as a key part of the model architecture. I think that needs to change, so this post is attempt to write down some guidance. Consider it a work in progress; I’d be interested in your thoughts.
What’s the Question?
There are really two kinds of questions:
- How much detail do you want in your model? This is just the age-old problem of aggregation, which I won’t rehash in this post.
- How do the subscripts you’re using contribute to a transparent, operational description of the system?
It’s the latter I’m concerned with. In essence: how do you implement a given level of detail so that the array structure makes sense?
Terminology
A bit of Vensim-centric terminology:
- A subscript range is a list of elements that make up an array dimension:
- Food {range} : broccoli, banana, cucumber, cheese, salami {elements}
- A subrange is a subset of a subscript:
- Vegetables : broccoli, banana, cucumber
- Animal Products : cheese, salami
- A mapping is a way to get from one to many, or many to one:
- FoodSource : vegetable, animal -> (Food: Vegetables, Animal Products) {maps 2 FoodSources to the 5 elements of Food}
- Person : (Person1-Person5) -> Bank Account {maps 5 people to 5 bank accounts}
- Many-to-many mapping can be done by matrix operations.
The Proposed Rules
Like most rules, these are made to be broken, but only sparingly.
- Maximize the correspondence between the model and the real world.
The point of good SD modeling is to create an operational, causal description of how the world works, which requires a 1:1 mapping between concepts in the model and concepts in reality. Subscripts, like everything else in the model, should support this. (Note that this differs a lot from the approach in, say, neural networks, which maximize statistical correspondence without worrying about the conceptual mapping at all.)
- Preserve the utility of the diagram as visual documentation of model structure.
This probably can’t be done fully without changing the diagram formalism, but it’s an underlying goal of many of the following rules. Careful organization of subscripts and equation structure can certainly avoid many problems.
- A subscript element should represent only one thing in the real world. Each thing in the real world should be represented by only one subscript element.
A practical example: if you have a dimension that represents individual people, don’t reuse it to represent bank accounts, unless there’s really a one to one relationship between people and accounts.
- As much structure as possible should be generic across all the elements of a range.
Vensim lets you write idiosyncratic equations for individual elements or subranges of a subscript (I think other languages do, too). But just because you can do it doesn’t mean you should do it. Sometimes it makes sense, as in marketShare[firm1] = 1-marketshare[firm2]. But if you make heavy use of these exceptions, the variable’s definition or interpretation gets stretched thin.
- All the elements of a subscript should be defined (no writing equations that define only a subrange, leaving other elements undefined).
This rule, and the previous one, exist largely in support of #1. When the user looks a the diagram, they expect to see generic structure. If vegetables and animal products have different causal structure, it’s probably better to build distinct structures with separate dimensions, rather than multiple structures that each define a subrange of some master range. (In Vensim, empty subranges also waste memory, though that’s a minor matter.)
- Don’t change the level of detail within a tightly-connected block of structure, especially a stock-flow chain.
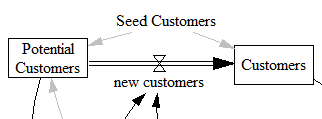
I’ll illustrate this one with an exception.
In this variant of the Bass model, customers are subscripted by company, because multiple companies are competing for customers. But there’s only one stock of potential customers in the marketplace. So, the flow of new customers adoption adds to customers for each company individually, but the summation across companies, SUM(new customers[company!]), is deducted from potential customers.
In this simple case, changing the level of aggregation within the stock-flow chain is handy. But if you overuse such transformations, it just becomes confusing.
- Minimize mapping.
- Map at the edges of subsystems.
Every mapping is essentially a transaction or transformation from one level of detail to another. Therefore, these mappings should be infrequent, and they should occur at the boundaries between sectors or subsystems of a model.
Ventity
Ventity changes all the rules, in a way that makes things much clearer, I think. Detail is not a property of individual equations, and in fact there are no arrays at all. Instead, detail is a property of a chunk of structure: an entity. All of the parts of a Firm belong to a Firm entity, identified by a FirmID (or some other unique tag). I think this is a challenge for beginners (myself included). Here’s an example.
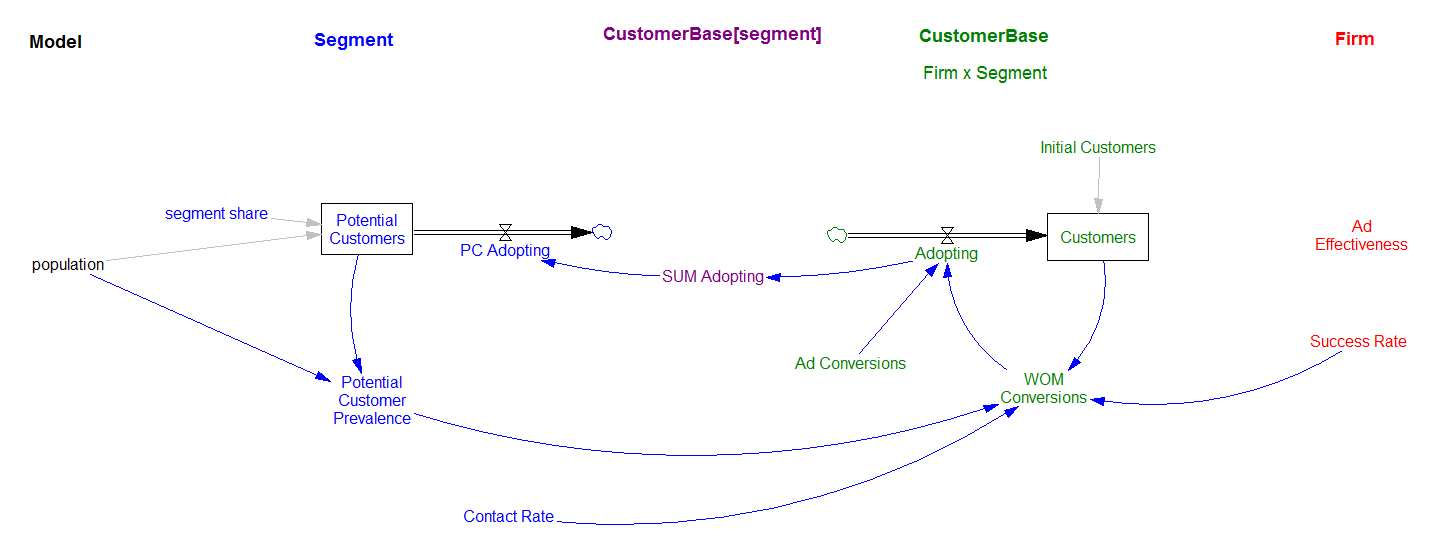
A few years ago, I replicated a multi-firm competitive dynamics model, based on the Bass model but with multiple firms and market segments (taking the one in Rule #5 one step further). Looking at the dimensions in the Vensim version, you might conclude that there are two “things” – firms and segments:
When I implemented the model in Ventity, I realized that there’s a crucial third “thing” – the relationship between segments and firms.
Each market segment (blue above) has one set of dynamics: depletion of potential customers. Each firm (red) has its own parameters and behaviors (in a more complete model, it would buy capacity, accumulate money, etc.). The relationship (green) captures the interactions between firms and segments, specifically, tracking the customers in a segment who have adopted the product of a firm.
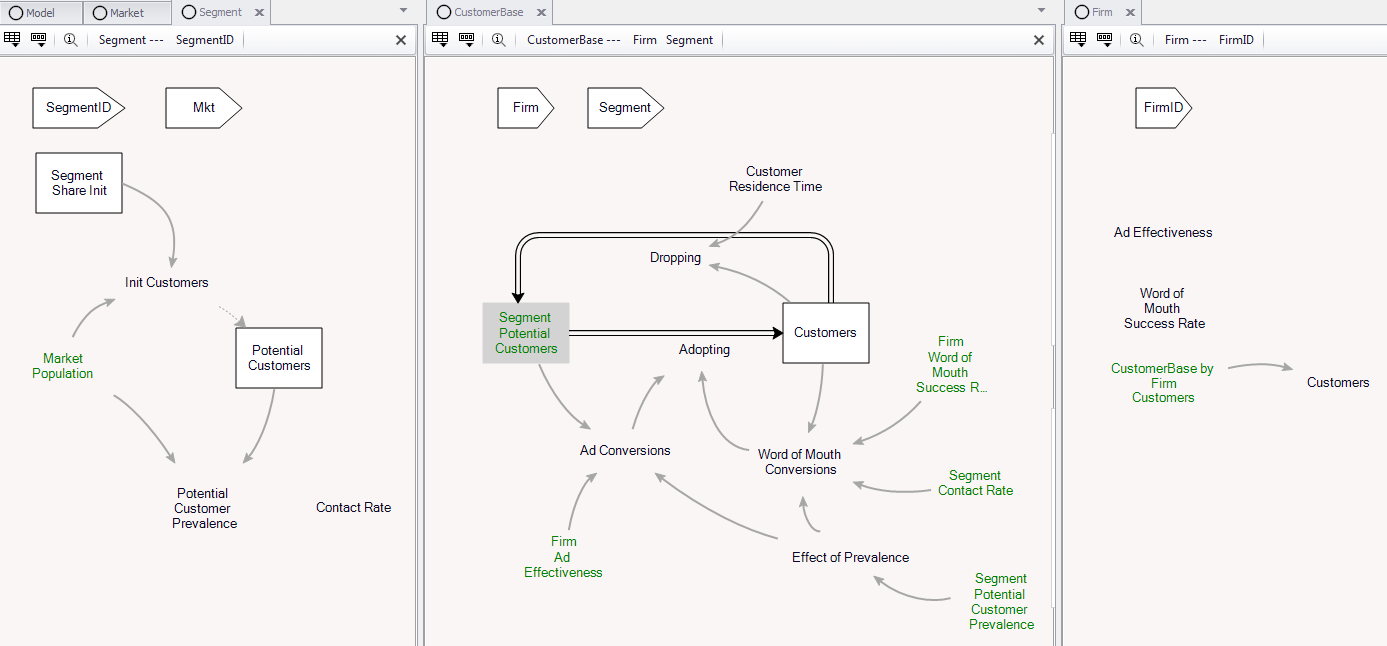
In the Ventity implementation, each set of structure lives in its own entity, with references (shadow variables) indicating the information flow from one level of detail to another.
Thinking about model structure in Ventity is a lot like designing the schema of a relational database. Once you know the entities (tables) needed and their key attributes (key fields), you know what relationships will be needed to connect them, and how to assign variables to a particular entity.
Even if you’re not using Ventity, I think this kind of thinking can help inform the design of models that use subscripts to represent detail complexity simply and clearly.
Thoughts?
Be sure to comment below. I suspect that other domains have already tackled this problem, so I’ll be very interested to hear about other ways of thinking about it.