Category: Aside

Excel, lost in the cloud

Excel is rapidly becoming unusable as Microsoft tries to shift everyone into the OneDrive/Sharepoint cloud. Here’s a very simple equation from a population model:

='https://ventanasystems-my.sharepoint.com/personal/vrbo_onmicrosoft_com/Documents/_Mkt/lxpgi/Model/Model/[Cohort Model Natural Increase.xlsx]Boston'!S135+'https://ventanasystems-my.sharepoint.com/personal/vrbo_onmicrosoft_com/Documents/_Mkt/lxpgi/Model/Model/[Cohort Model Immigration.xlsx]Boston'!S119+('https://ventanasystems-my.sharepoint.com/personal/vrbo_onmicrosoft_com/Documents/_Mkt/lxpgi/Model/Model/[Cohort Model NPR.xlsx]Boston'!S119-'https://ventanasystems-my.sharepoint.com/personal/vrbo_onmicrosoft_com/Documents/_Mkt/lxpgi/Model/Model/[Cohort Model.xlsx]Boston'!R119

URLs as equation terms? What were they thinking? This is an interface choice that makes things easy for programmers, and impossible for users.

A coronavirus prediction you can bank on

How many cases will there be on June 1? Beats me. But there’s one thing I’m sure of.

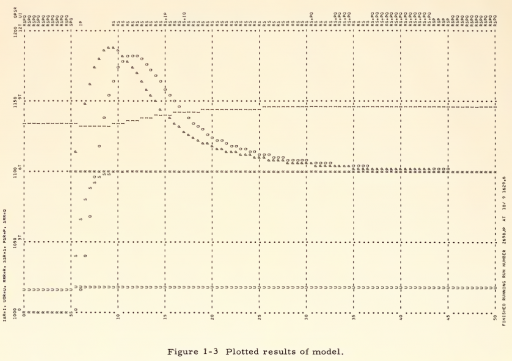
My confidence bounds on future behavior of the epidemic are still pretty wide. While there’s good reason to be optimistic about a lot of locations, there are also big uncertainties looming. No matter how things shake out, I’m confident in this:

The antiscience crowd will be out in force. They’ll cherry-pick the early model projections of an uncontrolled epidemic, and use that to claim that modelers predicted a catastrophe that didn’t happen, and conclude that there was never a problem. This is the Cassandra’s curse of all successful modeling interventions. (See Nobody Ever Gets Credit for Fixing Problems that Never Happened for a similar situation.)

But it won’t stop there. A lot of people don’t really care what the modelers actually said. They’ll just make stuff up. Just today I saw a comment at the Bozeman Chronicle to the effect of, “if this was as bad as they said, we’d all be dead.” Of course that was never in the cards, or the models, but that doesn’t matter in Dunning Krugerland.

Modelers, be prepared for a lot more of this. I think we need to be thinking more about defensive measures, like forecast archiving and presentation of results only with confidence bounds attached. However, it’s hard to do that and to produce model results at a pace that keeps up with the evolution of the epidemic. That’s something we need more infrastructure for.

A puzzling bias against experimentation

Objecting to experiments that compare two unobjectionable policies or treatments

Randomized experiments have enormous potential to improve human welfare in many domains, including healthcare, education, finance, and public policy. However, such “A/B tests” are often criticized on ethical grounds even as similar, untested interventions are implemented without objection. We find robust evidence across 16 studies of 5,873 participants from three diverse populations spanning nine domains—from healthcare to autonomous vehicle design to poverty reduction—that people frequently rate A/B tests designed to establish the comparative effectiveness of two policies or treatments as inappropriate even when universally implementing either A or B, untested, is seen as appropriate. This “A/B effect” is as strong among those with higher educational attainment and science literacy and among relevant professionals. It persists even when there is no reason to prefer A to B and even when recipients are treated unequally and randomly in all conditions (A, B, and A/B). Several remaining explanations for the effect—a belief that consent is required to impose a policy on half of a population but not on the entire population; an aversion to controlled but not to uncontrolled experiments; and a proxy form of the illusion of knowledge (according to which randomized evaluations are unnecessary because experts already do or should know “what works”)—appear to contribute to the effect, but none dominates or fully accounts for it. We conclude that rigorously evaluating policies or treatments via pragmatic randomized trials may provoke greater objection than simply implementing those same policies or treatments untested.

Happy Pi Day

I like e day better, but I think I’m in the minority. Pi still makes many appearances in the analysis of dynamic systems. Anyway, here’s a cool video that links the two, avoiding the usual infinite series of Euler’s formula.

An older, shorter version is here.

Notice that the definition of e^x as a function satisfying f(x+y)=f(x)f(y) is much like reasoning from Reality Checks. The same logic gives rise to the Boltzmann distribution in the concept of temperature in partitions of thermodynamic systems.

DYNAMO

Today I was looking for DYNAMO documentation of the TRND macro. Lo and behold, archive.org has the second edition of the DYNAMO User Guide online. It reminds me that I was lucky to have missed the punch card era:

… but not quite lucky enough to miss timesharing and the teletype:

The computer under my desk today would have been the fastest in the world the year I finished my dissertation. We’ve come a long way.

Meta MetaSD

I was looking at my google stats the other day, curious what posts interest people most. The answer was surprising. Guess what’s #1?

It’s not “Are Causal Loop Diagrams Useful?” (That’s #2.)

It’s not what I’d consider my best technical work, like Bathtub Statistics or Fun with 1D Vector Fields.

It’s not about something controversial, like On Limits to Growth or The alien hail Mary, and other climate policy plays.

Nor is it a hot topic, like Data science meets the bottom line.

It’s not something practical, like Writing an SD Conference Paper.

#1 is the Fibonacci sequence, How Many Pairs of Rabbits Are Created by One Pair in One Year?

Go figure.

Problem Formulation

Nelson Repenning & colleagues have a nice new paper on problem formulation. It’s set in a manufacturing context, but the advice is as relevant for building models as for building motorcycles:

Anatomy of a Good Problem Statement
A good problem statement has five basic elements:
• it references something that the organization cares about and connects that element to a clear and specific goal or target;
• it contains a clear articulation of the gap between the current state and the goal;
• the key variables—the target, the current state and the gap—are quantifiable,if not immediately measurable;
• it is neutral as possible concerning possible diagnoses or solutions;
• it is sufficiently small in scope that you can tackle it quickly.