Models Archives - Page 5 of 8

Cumulative emissions, right and wrong

During C-ROADS development, we explored several ways of accounting for cumulative per capita emissions. One practice that seems to be widespread is to accumulate (integrate) emissions divided by population, i.e.

cumulative emissions per cap	= INTEGRAL( emissions per capita(t) )
	= INTEGRAL( emissions(t)/population(t) )

This is physically meaningless. Emissions per capita is an intensive variable, and you can’t average or accumulate intensive variables in this way. It’s like averaging the temperature of a duck and a supertanker without accounting for the tankers 100,000x greater mass.

A proper thing to do is integrate emissions, then divide by population:

cumulative emissions per cap

= INTEGRAL( emissions per capita(t) ) / population

That yields a physically meaningful number, interpreted as cumulative emissions of a nation per current inhabitant. That’s a bit like per capita national debt.

Continue reading “Cumulative emissions, right and wrong”

Fit to data, good or evil?

The following is another extended excerpt from Jim Thompson and Jim Hines’ work on financial guarantee programs. The motivation was a client request for comparison of modeling results to data. The report pushes back a little, explaining some important limitations of model-data comparisons (though it ultimately also fulfills the request). I have a slightly different perspective, which I’ll try to indicate with some comments, but on the whole I find this to be an insightful and provocative essay.

First and Foremost, we do not want to give credence to the erroneous belief that good models match historical time series and bad models don’t. Second, we do not want to over-emphasize the importance of modeling to the process which we have undertaken, nor to imply that modeling is an end-product.

In this report we indicate why a good match between simulated and historical time series is not always important or interesting and how it can be misleading Note we are talking about comparing model output and historical time series. We do not address the separate issue of the use of data in creating computer model. In fact, we made heavy use of data in constructing our model and interpreting the output — including first hand experience, interviews, written descriptions, and time series.

This is a key point. Models that don’t report fit to data are often accused of not using any. In fact, fit to numerical data is only one of a number of tests of model quality that can be performed. Alone, it’s rather weak. In a consulting engagement, I once ran across a marketing science model that yielded a spectacular fit of sales volume against data, given advertising, price, holidays, and other inputs – R^2 of .95 or so. It turns out that the model was a linear regression, with a “seasonality” parameter for every week. Because there were only 3 years of data, those 52 parameters were largely responsible for the good fit (R^2 fell to < .7 if they were omitted). The underlying model was a linear regression that failed all kinds of reality checks.

Continue reading “Fit to data, good or evil?”

The Obscure Art of Datamodeling in Vensim

There are lots of good reasons for building models without data. However, if you want to measure something (i.e. estimate model parameters), produce results that are closely calibrated to history, or drive your model with historical inputs, you need data. Most statistical modeling you’ll see involves static or dynamically simple models and well-behaved datasets: nice flat files with uniform time steps, units matching (or, alarmingly, ignored), and no missing points. Things are generally much messier with a system dynamics model, which typically has broad scope and (one would hope) lots of dynamics. The diversity of data needed to accompany a model presents several challenges:

disagreement among sources
missing data points
non-uniform time intervals
variable quality of measurements
diverse source formats (spreadsheets, text files, databases)

The mathematics for handling the technical estimation problems were developed by Fred Schweppe and others at MIT decades ago. David Peterson’s thesis lays out the details for SD-type models, and most of the functionality described is built into Vensim. It’s also possible, of course, to go a simpler route; even hand calibration is often effective and reasonably quick when coupled with Synthesim.

Either way, you have to get your data corralled first. For a simple model, I’ll build the data right into the dynamic model. But for complicated models, I usually don’t want the main model bogged down with units conversions and links to a zillion files. In that case, I first build a separate datamodel, which does all the integration and passes cleaned-up series to the main model as a fast binary file (an ordinary Vensim .vdf). In creating the data infrastructure, I try to maximize three things:

Replicability. Minimize the number of manual steps in the process by making the data model do everything. Connect the datamodel directly to primary sources, in formats as close as possible to the original. Automate multiple steps with command scripts. Never use hand calculations scribbled on a piece of paper, unless you’re scrupulous about lab notebooks, or note the details in equations’ documentation field.
Transparency. Often this means “don’t do complex calculations in spreadsheets.” Spreadsheets are very good at some things, like serving as a data container that gives good visibility. However, spreadsheet calculations are error-prone and hard to audit. So, I try to do everything, from units conversions to interpolation, in Vensim.
Quality.#1 and #2 already go a long way toward ensuring quality. However, it’s possible to go further. First, actually look at the data. Take time to build a panel of on-screen graphs so that problems are instantly visible. Use a statistics or visualization package to explore it. Lately, I’ve been going a step farther, by writing Reality Checks to automatically test for discontinuities and other undesirable properties of spliced time series. This works well when the data is simply to voluminous to check manually.

This can be quite a bit of work up front, but the payoff is large: less model rework later, easy updates, and higher quality. It’s also easier generate graphics or statistics that help others to gain confidence in the model, though it’s sometimes important to help them recognize that goodness of fit is a weak test of quality.

It’s good to build the data infrastructure before you start modeling, because that way your drivers and quality control checks are in place as you build structure, so you avoid the pitfalls of an end-of-pipe inspection process. A frequent finding in our corporate work has been that cherished data is in fact rubbish, or means something quite different that what users have historically assumed. Ventana colleague Bill Arthur argues that modern IT practices are making the situation worse, not better, because firms aren’t retaining data as long (perhaps a misplaced side effect of a mania for freshness).

Continue reading “The Obscure Art of Datamodeling in Vensim”

GAMS Rant

I’ve just been looking into replicating the DICE-2007 model in Vensim (as I’ve previously done with DICE and RICE). As usual, it’s in GAMS, which is very powerful for optimization and general equilibrium work. However, it has to be the most horrible language I’ve ever seen for specifying dynamic models – worse than Excel, BASIC, you name it. The only contender for the title of time series horror show I can think of is SQL. I was recently amused when a GAMS user in China, working with a complex, unfinished Vensim model, heavy on arrays and interface detail, 50x the size of DICE, exclaimed, “it’s so easy!” I’d rather go to the dentist than plow through yet another pile of GAMS code to figure out what gsig(T)=gsigma*EXP(-dsig*10*(ORD(T)-1)-dsig2*10*((ord(t)-1)**2));sigma(“1”)=sig0;LOOP(T,sigma(T+1)=(sigma(T)/((1-gsig(T+1))));); means. End rant.

The other bathtubs – population

I’ve written quite a bit about bathtub dynamics here. I got the term from “Cloudy Skies” and other work by John Sterman and Linda Booth Sweeney.

We report experiments assessing people’s intuitive understanding of climate change. We presented highly educated graduate students with descriptions of greenhouse warming drawn from the IPCC’s nontechnical reports. Subjects were then asked to identify the likely response to various scenarios for CO2 emissions or concentrations. The tasks require no mathematics, only an understanding of stocks and flows and basic facts about climate change. Overall performance was poor. Subjects often select trajectories that violate conservation of matter. Many believe temperature responds immediately to changes in CO2 emissions or concentrations. Still more believe that stabilizing emissions near current rates would stabilize the climate, when in fact emissions would continue to exceed removal, increasing GHG concentrations and radiative forcing. Such beliefs support wait and see policies, but violate basic laws of physics.

The climate bathtubs are really a chain of stock processes: accumulation of CO2 in the atmosphere, accumulation of heat in the global system, and accumulation of meltwater in the oceans. How we respond to those, i.e. our emissions trajectory, is conditioned by some additional bathtubs: population, capital, and technology. This post is a quick look at the first.

I’ve grabbed the population sector from the World3 model. Regardless of what you think of World3’s economics, there’s not much to complain about in the population sector. It looks like this:

People are categorized into young, reproductive age, working age, and older groups. This 4th order structure doesn’t really capture the low dispersion of the true calendar aging process, but it’s more than enough for understanding the momentum of a population. If you think of the population in aggregate (the sum of the four boxes), it’s a bathtub that fills as long as births exceed deaths. Roughly tuned to history and projections, the bathtub fills until the end of the century, but at a diminishing rate as the gap between births and deaths closes:

Notice that the young (blue) peak in 2030 or so, long before the older groups come into near-equilibrium. An aging chain like this has a lot of momentum. A simple experiment makes that momentum visible. Suppose that, as of 2010, fertility suddenly falls to slightly below replacement levels, about 2.1 children per couple. (This is implemented by changing the total fertility lookup). That requires a dramatic shift in birth rates:

However, that doesn’t translate to an immediate equilibrium in population. Instead,population still grows to the end of the century, but reaching a lower level. Growth continues because the aging chain is internally out of equilibrium (there’s also a small contribution from ongoing extension of life expectancy, but it’s not important here). Because growth has been ongoing, the demographic pyramid is skewed toward the young. So, while fertility is constant per person of child-bearing age, the population of prospective parents grows for a while as the young grow up, and thus births continue to increase. Also, at the time of the experiment, the elderly population has not reached equilibrium given rising life expectancy and growth down the chain.

Achieving immediate equilibrium in population would require a much more radical fall in fertility, in order to bring births immediately in line with deaths. Implementing such a change would require shifting yet another bathtub – culture – in a way that seems unlikely to happen quickly. It would also have economic side effects. Often, you hear calls for more population growth, so that there will be more kids to pay social security and care for the elderly. However, that’s not the first effect of accelerated declines in fertility. If you look at the dependency ratio (the ratio of the very young and old to everyone else), the first effect of declining fertility is actually a net benefit (except to the extent that young children are intrinsically valued, or working in sweatshops making fake Gucci wallets):

The bottom line of all this is that, like other bathtubs, it’s hard to change population quickly, partly because of the physics of accumulation of people, and partly because it’s hard to even talk about the culture of fertility (and the economic factors that influence it). Population isn’t likely to contribute much to meeting 2020 emissions targets, but it’s part of the long game. If you want to win the long game, you have to anticipate long delays, which means getting started now.

The model (Vensim binary, text, and published formats): World3 Population.vmf World3-Population.mdl World3 Population.vpm

More climate models you can run

Following up on my earlier post, a few more on the menu:

SiMCaP – A simple tool for exploring emissions pathways, climate sensitivity, etc.

PRIMAP 2C Check Tool – A dirt-simple spreadsheet, exploiting the fact that cumulative emissions are a pretty good predictor of temperature outcomes along plausible emissions trajectories.

EdGCM – A full 3D model, for those who feel the need to get physical.

Last but not least, C-LEARN runs on the web. Desktop C-ROADS software is in the development pipeline.

Strategic Excess? Breakthrough's Nightmare?

Since it was the Breakthrough analysis that got me started on this topic, I took a quick look at it again. Their basic objection is:

Therein lies a Catch-22 of ACES: if the annual use of up to 2 billion tons of offsets permitted by the bill is limited due to a restricted supply of affordable offsets, the government will pick up the slack by selling reserve allowances, and “refill” the reserve pool with international forestry offset allowances later. […]

The strategic allowance reserve would be established by taking a certain percentage of allowances originally reserved for the future — 1% of 2012-2019 allowances, 2% of 2020-2029 allowances, and 3% of 2030-2050 allowances — for a total size of 2.7 billion allowances. Every year throughout the cap and trade program, a certain portion of this reserve account would be available for purchase by polluters as a “safety valve” in case the price of emission allowances rises too high.

How much of the reserve account would be available for purchase, and for what price? The bill defines the reserve auction limit as 5 percent of total emissions allowances allocated for any given year between 2012-2016, and 10 percent thereafter, for a total of 12 billion cumulative allowances. For example, the bill specifies that 5.38 billion allowances are to be allocated in 2017 for “capped” sectors of the economy, which means 538 million reserve allowances could be auctioned in that year (10% of 5.38 billion). In other words, the emissions “cap” could be raised by 10% in any year after 2016.

First, it’s not clear to me that international offset supply for refilling the reserve is unlimited. Section 726 doesn’t say they’re unlimited, and a global limit of 1 to 1.5 GtCO2eq/yr applies elsewhere. Anyhow, given the current scale of the offset market, it’s likely that reserve refilling will be competing with market participants for a limited supply of allowances.

Second, even if offset refills do raise the de facto cap, that doesn’t raise global emissions, except to the extent that offsets aren’t real, additional and all that. With perfect offsets, global emissions would go down due to the 5:4 exchange ratio of offsets for allowances. If offsets are really rip-offsets, then W-M has bigger problems than the strategic reserve refill.

Third, and most importantly, the problem isn’t oversupply of allowances through the reserve. Instead, it’s hard to get allowances out of the reserve – they check in, and never check out. Simple math suggests, and simulations confirm, that it’s hard to generate a price trajectory yielding sustained auction release. Here’s a test with 3%/yr BAU emissions growth and 10% underlying demand volatility:

Even with these implausibly high drivers, it’s hard to get a price trajectory that triggers a sustained auction flow, and total allowance supply (green) and emissions hardly differ from from the no-reserve case.

My preliminary simulation experiments suggest that it’s very unlikely that Breakthrough’s nightmare, a 10% cap violation, could really occur. To make that happen overall, you’d need sustained price increases of over 20% per year – i.e., an allowance price of $56,000/TonCO2eq in 2050. However, there are lesser nightmares hidden in the convoluted language – a messy program to administer, that in the end fails to mitigate volatility.

Strategic Excess? Insights

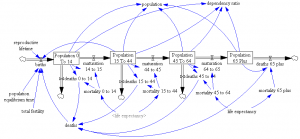
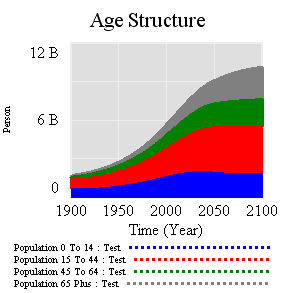
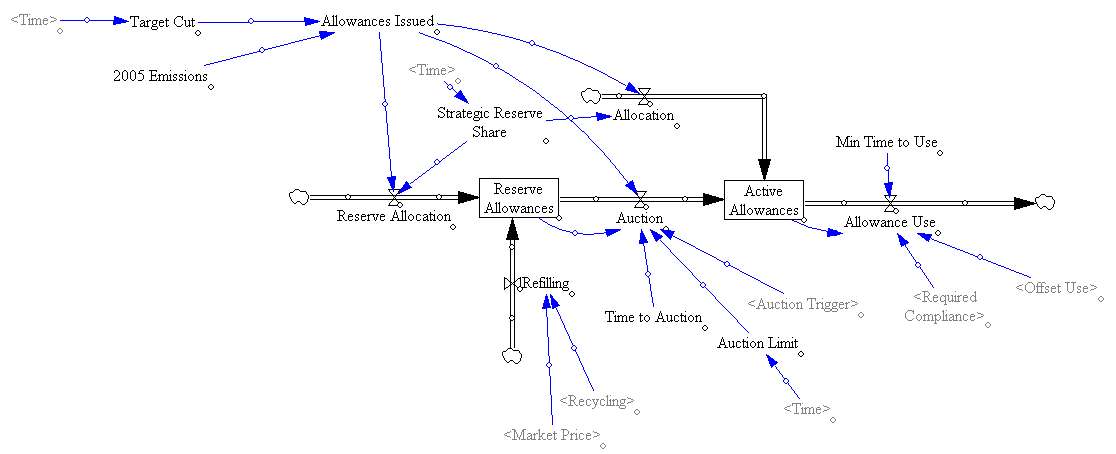
Model in hand, I tried some experiments (actually I built the model iteratively, while experimenting, but it’s hard to write that way, so I’m retracing my steps).

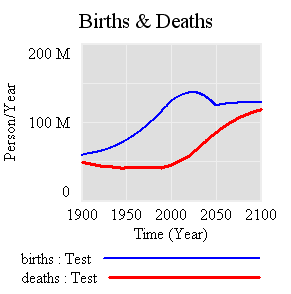
First, the “general equilbrium equivalent” version: no volatility, no SR marginal cost penalty for surprise, and firms see the policy coming. Result: smooth price escalation, and the strategic reserve is never triggered. Allowances just pile up in the reserve:

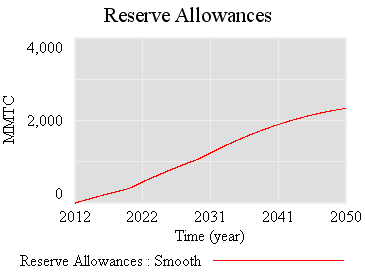
Since allowances accumulate, the de facto cap is 1-3% lower (by the share of allowances allocated to the reserve).

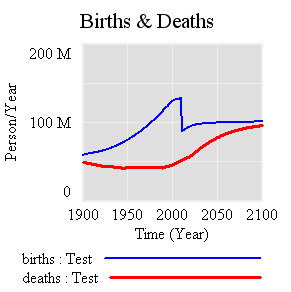
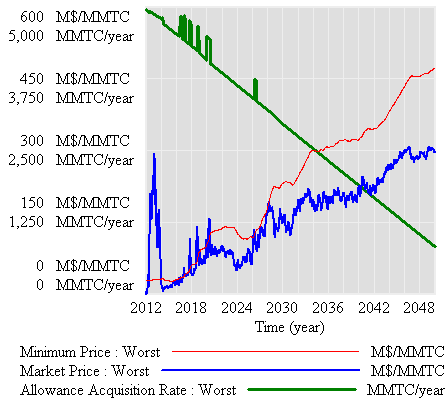
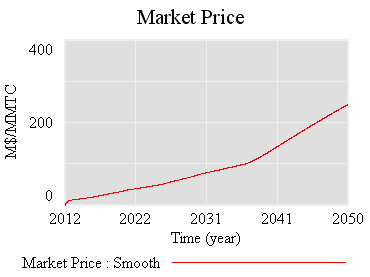
If there’s noise (SD=4.4%, comparable to petroleum demand), imperfect foresight, and short run adjustment costs, the market is more volatile:

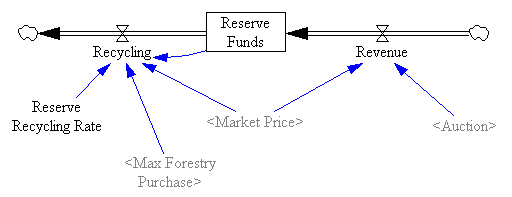
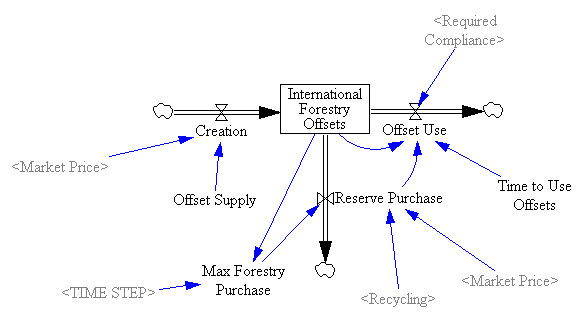
However, something strange happens. The stock of reserve allowances actually increases, even though some reserves are auctioned intermittently. That’s due to the refilling mechanism. An early auction, plus overreaction by firms, triggers a near-collapse in allowance prices (as happened in the ETS). Thus revenues generated in the reserve auction at high prices used to buy a lot of forestry offsets at very low prices:

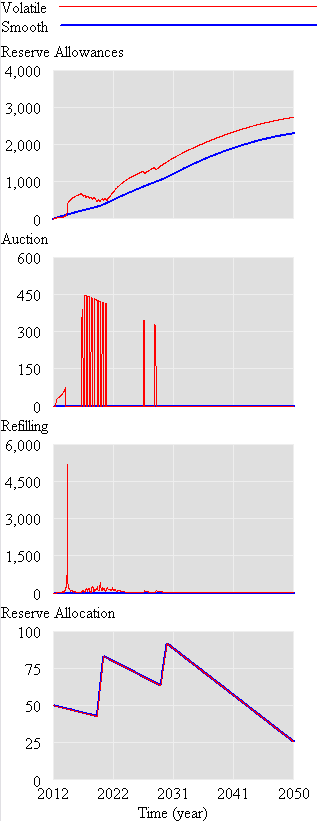
Could this happen in reality? I’m not sure – it depends on timing, behavior, and details of the recycling implementation. I think it’s safe to say that the current design is not robust to such phenomena. Fortunately, the market impact over the long haul is not great, because the extra accumulated allowances don’t get used (they pile up, as in the smooth case).

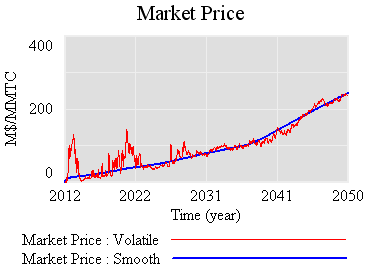
So, what is the reserve really accomplishing? Not much, it seems. Here’s the same trajectory, with volatility but no strategic reserve system:

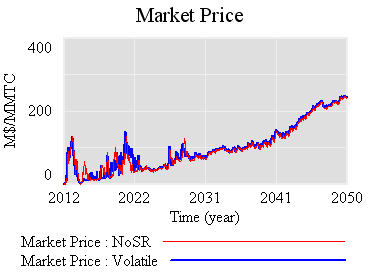
The mean price with the reserve (blue) is actually slightly higher, because the reserve mainly squirrels away allowances, without ever releasing them. Volatility is qualitatively the same, if not worse. That doesn’t seem like a good trade (unless you like the de facto emissions cut, which could be achieved more easily by lowering the cap and scrapping the reserve mechanism).

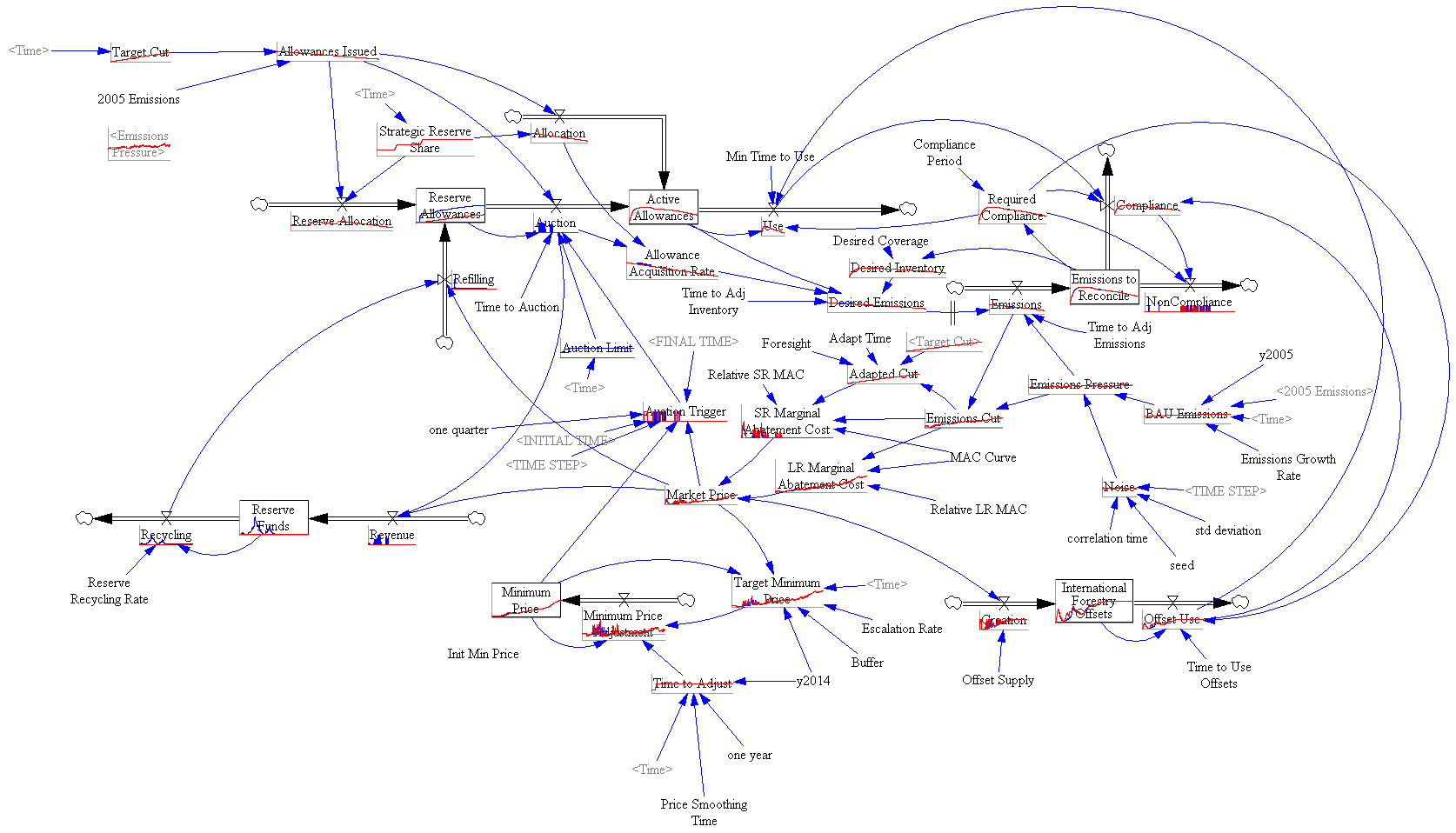
One reason the reserve fails to achieve its objectives is the recycling mechanism, which creates a perverse feedback loop that offsets the strategic reserve’s intended effect:

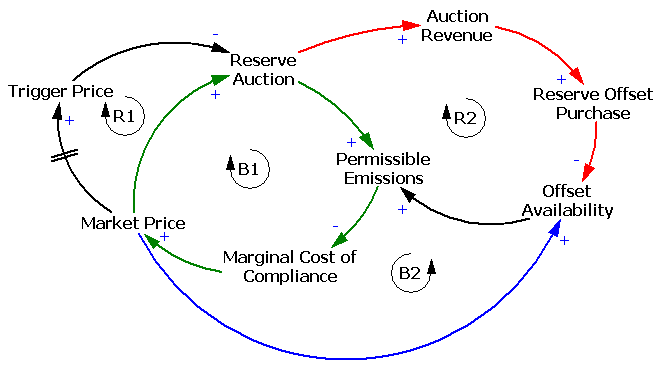
The intent of the reserve is to add a balancing feedback loop (B2, green) that stabilizes price. The problem is, the recycling mechanism (R2, red) consumes international forestry offsets that would otherwise be available for compliance, thus working against normal market operations (B2, blue). Thus the mechanism is only helpful to the extent that it exploits clever timing (doubtful), has access to offsets unavailable to the broad market (also doubtful), or doesn’t recycle revenue to refill the reserve. If you have a reserve, but don’t refill, you get some benefit:

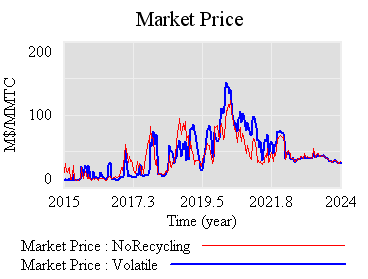
Still, the reserve mechanism seems like a lot of complexity yielding little benefit. At best, it can iron out some wrinkles, but it does nothing about strong, sustained price excursions (due to picking an infeasible target, for example). Perhaps there is some other design that could perform better, by releasing and refilling the reserve in a more balanced fashion. That ideal starts to sound like “buy low, sell high” – which is what speculators in the market are supposed to do. So, again, why bother?

I suspect that a more likely candidate for stabilization, robust to uncertainty, involves some possible violation of the absolute cap (gasp!). Realistically, if there are sustained price excursions, congress will violate it for us, so perhaps its better to recognize that up front and codify some orderly process for adaptation. At the least, I think congress should scrap the current reserve, and write the legislation in such a way as to kick the design problem to EPA, subject to a few general goals. That way, at least there’d be time to think about the design properly.

Strategic Excess? The Model

It’s hard to get an intuitive grasp on the strategic reserve design, so I built a model (which I’m not posting because it’s still rather crude, but will describe in some detail). First, I’ll point out that the model has to be behavioral, dynamic, and stochastic. The whole point of the strategic reserve is to iron out problems that surface due to surprises or the cumulative effects of agent misperceptions of the allowance market. You’re not going to get a lot of insight about this kind of situation from a CGE or intertemporal optimization model – which is troubling because all the W-M analysis I’ve seen uses equilibrium tools. That means that the strategic reserve design is either intuitive or based on some well-hidden analysis.

Here’s one version of my sketch of market operations (click to enlarge):

It’s already complicated, but actually less complicated than the mechanism described in W-M. For one thing, I’ve made some process continuous (compliance on a rolling basis, rather than at intervals) that sound like they will be discrete in the real implementation.

The strategic reserve is basically a pool of allowances withheld from the market, until need arises, at which point they are auctioned and become part of the active allowance pool, usable for compliance:

Reserves auctioned are – to some extent – replaced by recycling of the auction revenue:

Refilling the strategic reserve consumes international forestry offsets, which may also be consumed by firms for compliance. Offsets are created by entrepreneurs, with supply dependent on market price.

Auctions are triggered when market prices exceed a threshold, set according to smoothed actual prices:

(Actually I should have labeled this Maximum, not Minimum, since it’s a ceiling, not a floor.)

The compliance market is a bit complicated. Basically, there’s an aggregate firm that emits, and consumes offsets or allowances to cover its compliance obligation for those emissions (non-compliance is also possible, but doesn’t occur in practice; presumably W-M specifies a penalty). The firm plans its emissions to conform to the expected supply of allowances. The market price emerges from the marginal cost of compliance, which has long run and short run components. The LR component is based on eyeballing the MAC curve in the EPA W-M analysis. The SR component is arbitrarily 10x that, i.e. short term compliance surprises are 10x as costly (or the SR elasticity is 10x lower). Unconstrained firms would emit at a BAU level which is driven by a trend plus pink noise (the latter presumably originating from the business cyle, seasonality, etc.).

So far, so good. Next up: experiments.

Good modeling practices

Some thoughts I’ve been collecting, primarily oriented toward system dynamics modeling in Vensim, but relevant to any modeling endeavor:

Know why you’re building the model.
- If you’re targeting a presentation or paper, write the skeleton first, so you know how the model will fill in the answers as you go.
Organize your data first.
- No data? No problem. But surely you have some reference mode in mind, and some constraints on behavior, at least in extreme conditions.
- In Vensim, dump it all into a spreadsheet, database, or text file and import it into a data model, using the Model>Import data… feature, GET XLS DATA functions, or ODBC.
- Don’t put data in lookups (table functions) unless you must for some technical reason; they’re a hassle to edit and update, and lousy at distinguishing real data points from interpolation.
Keep a lab notebook. An open word processor while you work is useful. Write down hypotheses before you run, so that you won’t rationalize surprises. Continue reading “Good modeling practices”