I ran across this cool article on network dynamics, and thought the model would be an interesting application for Ventity:
Coupled catastrophes: sudden shifts cascade and hop among interdependent systems
Charles D. Brummitt, George Barnett and Raissa M. D’Souza
Abstract
An important challenge in several disciplines is to understand how sudden changes can propagate among coupled systems. Examples include the synchronization of business cycles, population collapse in patchy ecosystems, markets shifting to a new technology platform, collapses in prices and in confidence in financial markets, and protests erupting in multiple countries. A number of mathematical models of these phenomena have multiple equilibria separated by saddle-node bifurcations. We study this behaviour in its normal form as fast–slow ordinary differential equations. In our model, a system consists of multiple subsystems, such as countries in the global economy or patches of an ecosystem. Each subsystem is described by a scalar quantity, such as economic output or population, that undergoes sudden changes via saddle-node bifurcations. The subsystems are coupled via their scalar quantity (e.g. trade couples economic output; diffusion couples populations); that coupling moves the locations of their bifurcations. The model demonstrates two ways in which sudden changes can propagate: they can cascade (one causing the next), or they can hop over subsystems. The latter is absent from classic models of cascades. For an application, we study the Arab Spring protests. After connecting the model to sociological theories that have bistability, we use socioeconomic data to estimate relative proximities to tipping points and Facebook data to estimate couplings among countries. We find that although protests tend to spread locally, they also seem to ‘hop’ over countries, like in the stylized model; this result highlights a new class of temporal motifs in longitudinal network datasets.
Ventity makes sense here because the system consists of a network of coupled states. Ventity makes it easy to represent a wide variety of network architectures. This means there are two types of entities in the system: “Nodes” and “Couplings.”
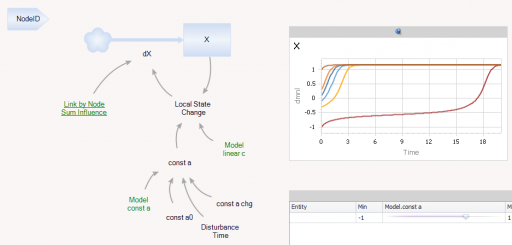
The Node entitytype contains a single state (X), with local feedback, as well as a remote influence from Coupling and a few global parameters referenced from the Model entity:
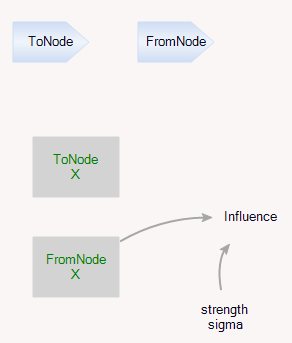
A Coupling is simply a reference from one Node to another, with a strength parameter:
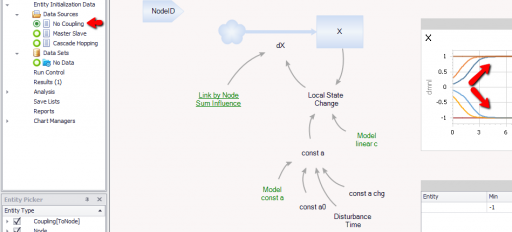
If you don’t create any Couplings, the Nodes run standalone, as in Section 2.1 of the paper. You can use that to see how the bistable dynamics of X create a tipping point, by running a set of nodes with different initial conditions:
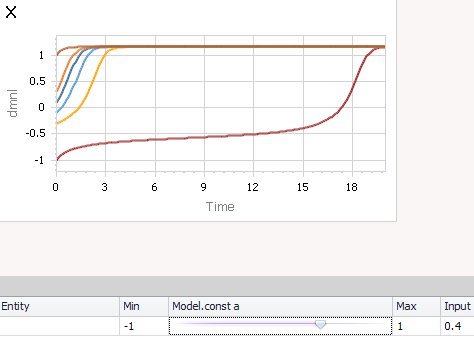
By increasing the global Model.const a, you can induce a bifurcation that destabilizes the lower branch of the system, so that all trajectories tend to increase:
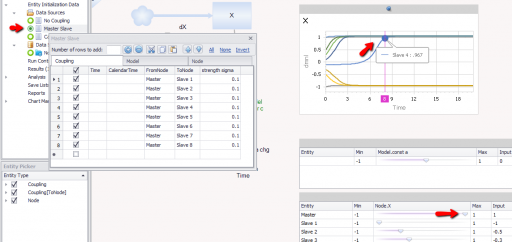
Section 2.2 of the paper illustrates a master-slave system, with two Nodes and a single Coupling by which the master Node influences the Slave. I actually set this up with a single master driving multiple slaves, where each slave has a different initial X. Then increasing the master’s initial X spills over to shift the stability of Slave 4’s initial state:
In Section 2.3, things get really interesting, with cascade hopping. In this scenario, there are three coupled Nodes, X -> Y -> Z. X (blue) is disturbed exogenously by changing its local const a parameter at time 8, causing it to transition from a stable value near 1 to about -1.2. This in turn influences a slight shift in Y’s state (red), but due to weak coupling that’s not enough to destabilize Y. However, the small shift in Y is enough to nudge Z out of its state, causing a sudden transition to -1.2 around time 18.
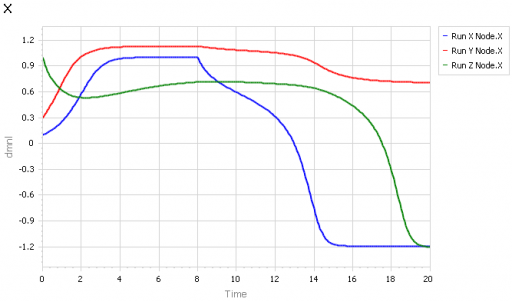
Consider what this would do to any simple correlation-based thinking, or a regression model. X has clearly caused a catastrophic change in Z, but without much of an obvious change in Y. In the presence of noise, it would be easy to conclude that this was all a coincidence. (If you harbor any doubt about the causality, just set Node X’s const a chg to zero and see what happens.)
I encourage you to take a look at the original paper – it has some nice phase diagrams and goes on to consider some interesting applications. I think the same structure could be used to implement another interesting network dynamics paper: State-dependent effective interactions in oscillator networks through coupling functions with dead zones. And if you like the topic, Network Catastrophe: Self-Organized Patterns Reveal both the Instability and the Structure of Complex Networks has more interesting data-centric applications.
An interesting extension of this model would be to generalize to larger networks, by modifying the input data or using actions to generate random networks.
The model: SaddleNodeNetwork4.zip

1 thought on “Coupled Catastrophes”