Tag: uncertainty

Sources of Uncertainty

The confidence bounds I showed in my previous post have some interesting features. The following plots show three sources of the uncertainty in simulated surveillance for Chronic Wasting Disease in deer.

  • Parameter uncertainty
  • Sampling error in the measurement process
  • Driving noise from random interactions in the population

You could add external disturbances like weather to this list, though we don’t simulate it here.

By way of background, this come from a fairly big model that combines the dynamics of the host (deer) with an SIR-like model of disease transmission and progression. There’s quite a bit of disaggregation (regions, ages, sexes). The model is driven by historic harvest and sample sizes, and generates deer population, vegetation, and disease dynamics endogenously. The parameters used here represent a Bayesian posterior, from MCMC with literature priors and a lot of data. The parameter sample from the posterior is a joint distribution that captures both individual parameter variation and covariation (though with only a few exceptions things seem to be relatively independent).

Here’s the effect of parameter uncertainty on the disease trajectory:

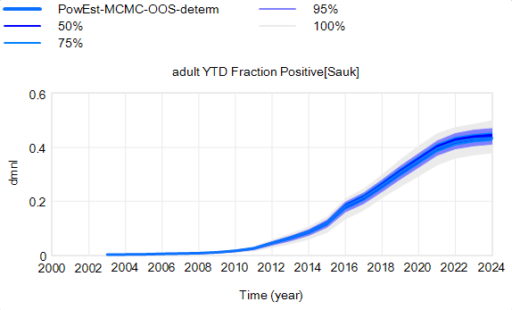Each of the 10,000 runs making up this ensemble is deterministic. It’s surprisingly tight, because it is well-determined by the data.

However, parameter uncertainty is not the only issue. Even if you know the actual state of the disease perfectly, there’s still uncertainty in the reported outcome due to sampling variation. You might stray from the “true” prevalence of the disease because of chance in the selection of which deer are actually tested. Making sampling stochastic broadens the bounds:

That’s still not the whole picture, because deer aren’t really deterministic. They come in integer quanta and they have random interactions. Thus a standard SD formulation like:

births = birth rate * doe population

becomes

births = Poisson( birth rate * doe population )

For stock outflows, like the transition from healthy to infected, the Binomial distribution may be the appropriate choice. This means there’s additional variance around the deterministic course, and the model can explore a wider set of trajectories.

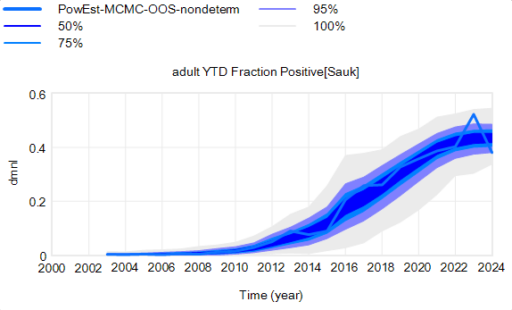There’s one other interesting feature, particularly evident in this last graph: uncertainty around the mean (i.e. the geometric standard deviation) varies quite a bit. Initially, uncertainty increases with time – as Yogi Berra said, “It’s tough to make predictions, especially about the future.” In the early stages of the disese (2003-2008 say), numbers are small and random events affect the timing of takeoff of the disease, amplified by future positive feedback. A deterministic disease model with reproduction ratio R0>1 can only grow, but in a stochastic model luck can cause the disease to go extinct or bumble around 0 prevalence for a while before emerging into growth. Towards the end of this simulation, the confidence bounds narrow. There are two reasons for this: negative feedback is starting to dominate as the disease approaches saturation prevalence, and at the same time the normalized standard deviation of the sampling errors and randomness in deer dynamics is decreasing as the numbers become larger (essentially with 1/sqrt(n)).

This is not uncommon in real systems. For example, you may be unsure where a chaotic pendulum will be in it’s swing a minute from now. But you can be pretty sure that after an hour or a day it will be hanging idle at dead center. However, this might not remain true when you broaden the boundary of the system to include additional feedbacks or disturbances. In this CWD model, for example, there’s some additional feedback from human behavior (not in the statistical model, but in the full version) that conditions the eventual saturation point, perhaps preventing convergence of uncertainty.

 

Calibrate your confidence bounds: an updated Capen Quiz

Forecasters are notoriously overconfident. This applies to nearly everyone who predicts anything, not just stock analysts. A few fields, like meteorology, have gotten a handle on the uncertainty in their forecasts, but this remains the exception rather than the rule.

Having no good quantitative idea of uncertainty, there is an almost universal tendency for people to understate it. Thus, they overestimate the precision of their own knowledge and contribute to decisions that later become subject to unwelcome surprises.

A solution to this problem involves some better understanding of how to treat uncertainties and a realization that our desire for preciseness in such an unpredictable world may be leading us astray.

E.C. Capen illustrated the problem in 1976 with a quiz that asks takers to state 90% confidence intervals for a variety of things – the length of the Golden Gate bridge, the number of cars in California, etc. A winning score is 9 out of 10 right. 10 out of 10 indicates that the taker was underconfident, choosing ranges that are too wide.

Ventana colleague Bill Arthur has been giving the quiz to clients for years. In fact, it turns out that the vast majority of takers are overconfident in their knowledge – they choose ranges that are too narrow, and get only a three or four questions right. CEOs are the worst – if you score zero out of 10, you’re c-suite material.

My kids and I took the test last year. Using what we learned, we expanded the variance on our guesses of the weight of a giant pumpkin at the local coop – and as a result, brought the monster home.

Now that I’ve taken the test a few times, it spoils the fun, so last time I was in a room for the event, I doodled an updated quiz. Here’s your chance to calibrate your confidence intervals:

For each question, specify a range (minimum and maximum value) within which you are 80% certain that the true answer lies. In other words, in an ideal set of responses, 8 out of 10 answers will contain the truth within your range.

Example*:

The question is, “what was the winning time in the first Tour de France bicycle race, in 1903?”

Your answer is, “between 1 hour and 1 day.”

Your answer is wrong, because the truth (94 hours, 33 minutes, 14 seconds) does not lie within your range.

Note that it doesn’t help to know a lot about the subject matter – precise knowledge merely requires you to narrow your intervals in order to be correct 80% of the time.

Now the questions:

  1. What is the wingspan of an Airbus A380-800 superjumbo jet?
  2. What is the mean distance from the earth to the moon?
  3. In what year did the Russians launch Sputnik?
  4. In what year did Alaric lead the Visigoths in the Sack of Rome?
  5. How many career home runs did baseball giant Babe Ruth hit?
  6. How many iPhones did Apple sell in FY 2007, its year of introduction?
  7. How many transistors were on a 1993 Intel Pentium CPU chip?
  8. How many sheep were in New Zealand on 30 June 2006?
  9. What is the USGA-regulated minimum diameter of a golf ball?
  10. How tall is Victoria Falls on the Zambezi River?

Be sure to write down your answers (otherwise it’s too easy to rationalize ex post). No googling!

Answers at the end of next week.

*Update: edited slightly for greater clarity.

MIT Updates Greenhouse Gamble

For some time, the MIT Joint Program has been using roulette wheels to communicate climate uncertainty. They’ve recently updated the wheels, based on new model projections:

No Policy Policy
New No policy Policy
Old Old no policy Old policy

The changes are rather dramatic, as you can see. The no-policy wheel looks like the old joke about playing Russian Roulette with an automatic. A tiny part of the difference is a baseline change, but most is not, as the report on the underlying modeling explains:

The new projections are considerably warmer than the 2003 projections, e.g., the median surface warming in 2091 to 2100 is 5.1°C compared to 2.4°C in the earlier study. Many changes contribute to the stronger warming; among the more important ones are taking into account the cooling in the second half of the 20th century due to volcanic eruptions for input parameter estimation and a more sophisticated method for projecting GDP growth which eliminated many low emission scenarios. However, if recently published data, suggesting stronger 20th century ocean warming, are used to determine the input climate parameters, the median projected warning at the end of the 21st century is only 4.1°C. Nevertheless all our simulations have a very small probability of warming less than 2.4°C, the lower bound of the IPCC AR4 projected likely range for the A1FI scenario, which has forcing very similar to our median projection.

I think the wheels are a cool idea, but I’d be curious to know how users respond to it. Do they cheat, and spin to get the outcome they hope for? Perhaps MIT should spice things up a bit, by programming an online version that gives users’ computers the BSOD if they roll a >7C world.

Hat tip to Travis Franck for pointing this out.

News Flash: There Is No "Environmental Certainty"

The principal benefit cited for cap & trade is “environmental certainty,” meaning that “a cap-and-trade system, coupled with adequate enforcement, assures that environmental goals actually would be achieved by a certain date.” Environmental certainty is a bit of a misnomer. I think of environmental certainty as ensuring a reasonable chance of avoiding serious climate impacts. What people mean when they’re talking about cap & trade is really “emissions certainty.” Unfortunately, emissions certainty doesn’t provide climate certainty:

Emissions trajectories yielding 2C temperature change

Even if we could determine a “safe” level of interference in the climate system, the sensitivity of global mean temperature to increasing atmospheric CO2 is known perhaps only to a factor of three or less. Here we show how a factor of three uncertainty in climate sensitivity introduces even greater uncertainty in allowable increases in atmospheric CO2 CO2 emissions. (Caldeira, Jain & Hoffert, Science)

The uncertainty about climate sensitivity (not to mention carbon cycle feedbacks and other tipping point phenomena) makes the emissions trajectory we need highly uncertain. That trajectory is also subject to other big uncertainties – technology, growth convergence, peak oil, etc. Together, those features make it silly to expend a lot of effort on detailed plans for 2050. We don’t need a ballistic trajectory; we need a guidance system. I’d like to see us agree to a price on GHGs everywhere now, along with a decision rule for adapting that price over time until we’re on a downward emissions trajectory. Then move on to the other legs of the stool: ensuring equitable opportunities for development, changing lifestyle, tackling institutional barriers to change, and investing in technology.

Unfortunately, cap & trade seems ill-suited to adaptive control. Emissions commitments and allowance allocations are set in multi-year intervals, announced in advance, with long lead times for design. Financial markets and industry players want that certainty, but the delay limits responsiveness. Decision makers don’t set the commitment by strictly environmental standards; they also ask themselves what allocation will result in an “acceptable” price. They’re risk averse, so they choose an allocation that’s very likely to lead to an acceptable price. That means that, more often than not, the system will be overallocated. On balance, their conservatism is probably a good thing; otherwise the whole system could unravel from a negative public reaction to volatile prices. Ironically, safety valves – one policy that could make cap & trade more robust, and thus enable better mean performance – are often opposed because they reduce emissions certainty.