Tag: CWD

Sometimes the best model is the data

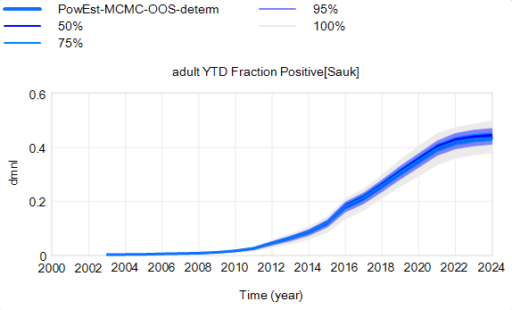
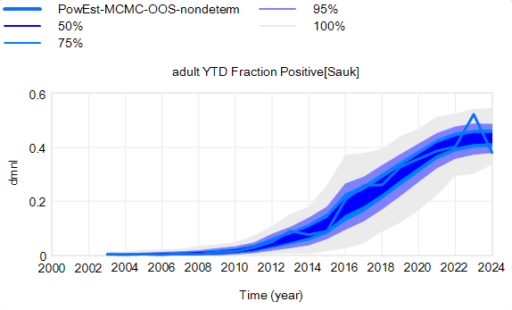
I’m working on Chronic Wasting Disease in deer in a couple US states. One interesting question is, what have historical management actions actually done to mitigate prevalence and spread of the disease?

We think we have pretty strong evidence that targeted removals and increased harvest of antlerless deer (lowering population density) have a substantial effect, though not many regions have been able to fully deploy these measures. Here’s one that’s been highly effective:

… and here’s one that’s less successful, due to low targeted removal rates and a later start:

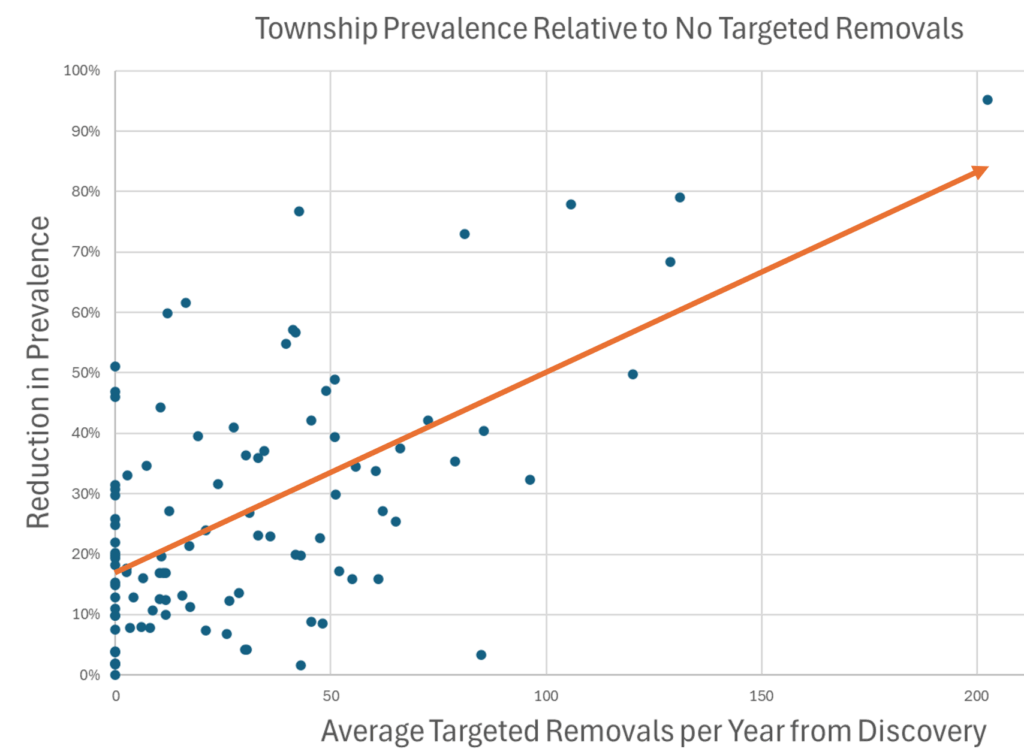
When you look at the result across lots of regions, there’s a clear pattern. More removals = lower prevalence, and even regions that received no treatment benefited due to geographic spillovers from deer dispersal.

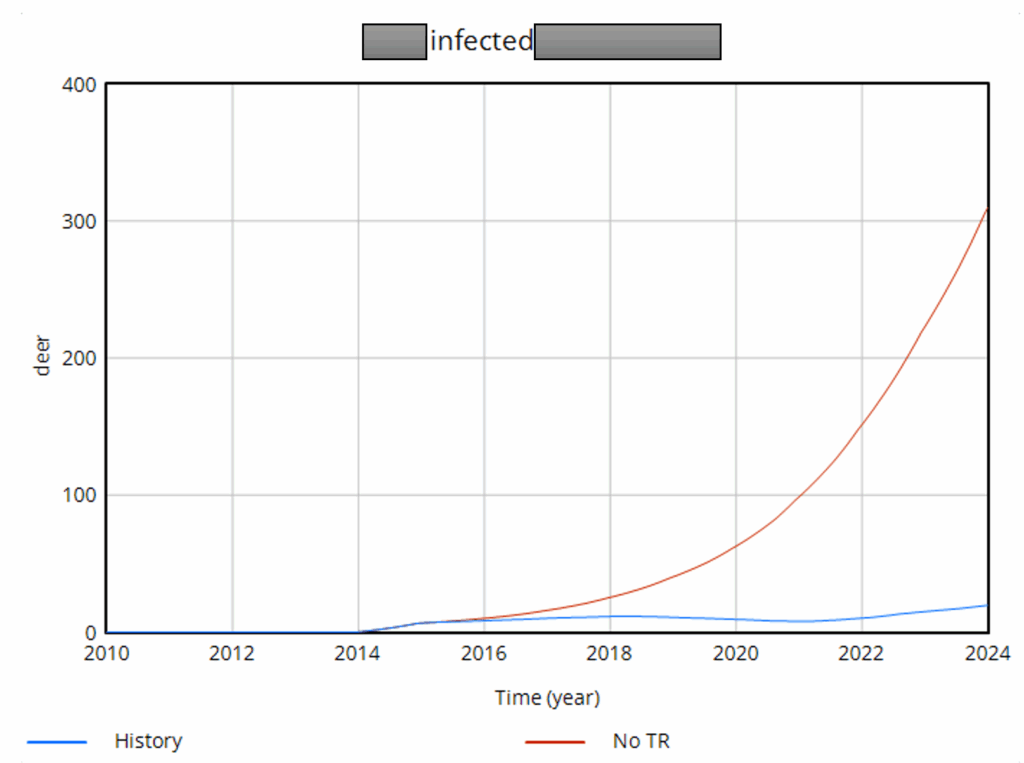
There’s a challenge with these results though: they’re all from simulations. There’s a good reason for that: most of the raw data is too noisy to be informative. Here’s some of the better data we have:

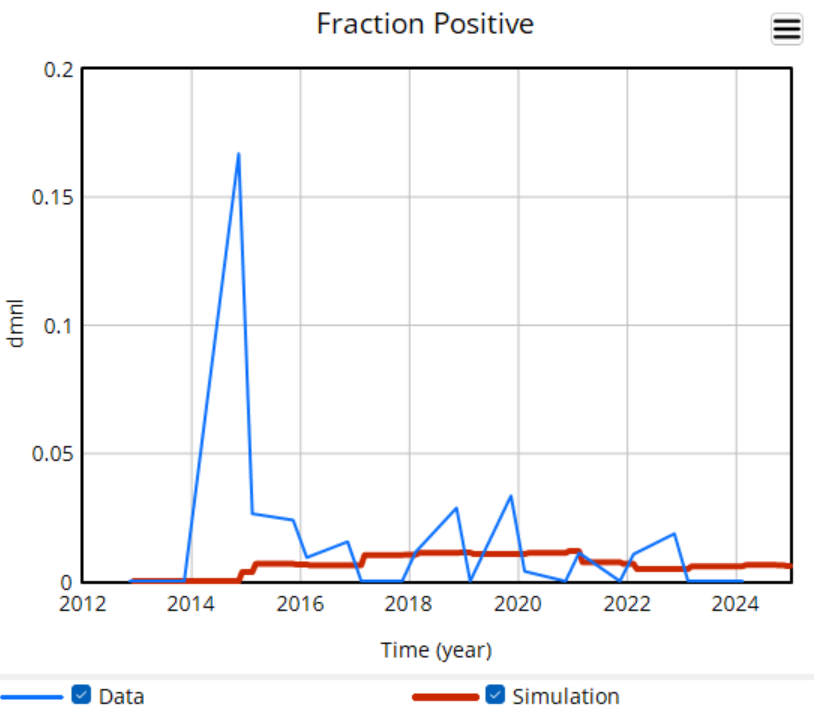
The noise in the data is inherent in sampling processes, and here it’s exacerbated by the fact that the sample size is small and varying a lot. The initial spike, for example, is a lucky discovery of 2 positive deer in a sample of 12. This makes it almost impossible to do sensible eyeball comparisons between regions in the raw data, and of course the data doesn’t include counterfactuals.

The model does do counterfactuals, but as soon as you show simulated results, you have a hill to climb. You have to explain what a model is and does, and what’s in the particular model in use. Some people may be skeptical (wrongly) of the very idea of a model. You may not have time for these conversations. So, one habit I’ve picked up from Ventana is to use the model result as a guide for where to look for compelling data that cleanly illustrates what the model is doing.

It turns out there is some in this case. Here are the histories of two regions that received different CWD management treatments, and had wildly different outcomes:

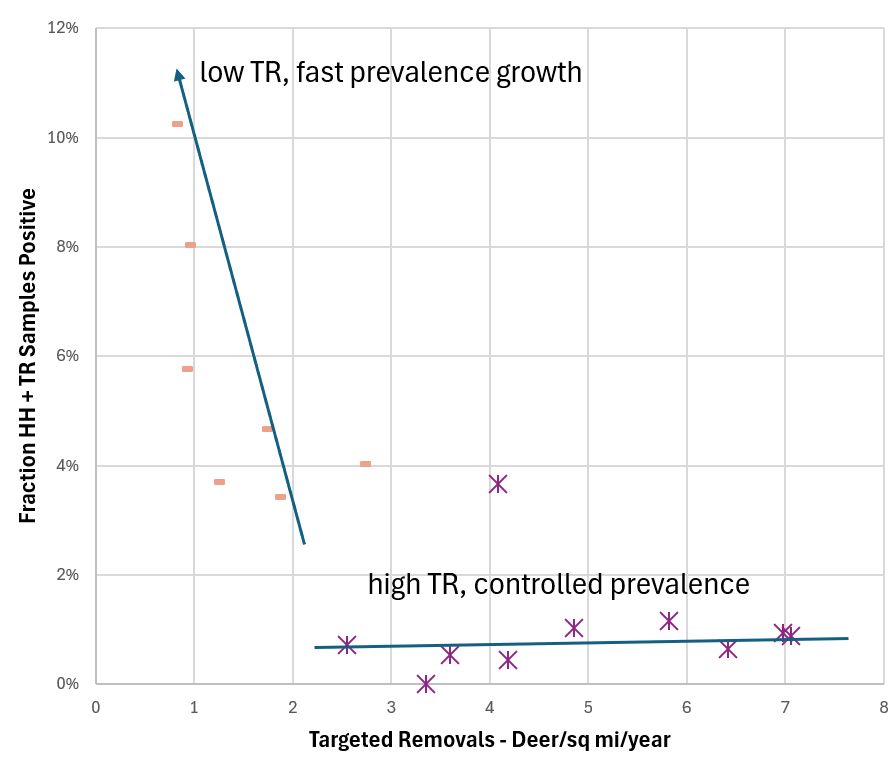
There are still some assumptions here – any interpretation of data is really a model – but I think this view is skeptic-resistant. It’s still not ideal, because scatterplots are less widely understood than time series plots, but I think it’s a useful complement to the simulation model results.

Sources of Uncertainty

The confidence bounds I showed in my previous post have some interesting features. The following plots show three sources of the uncertainty in simulated surveillance for Chronic Wasting Disease in deer.

  • Parameter uncertainty
  • Sampling error in the measurement process
  • Driving noise from random interactions in the population

You could add external disturbances like weather to this list, though we don’t simulate it here.

By way of background, this come from a fairly big model that combines the dynamics of the host (deer) with an SIR-like model of disease transmission and progression. There’s quite a bit of disaggregation (regions, ages, sexes). The model is driven by historic harvest and sample sizes, and generates deer population, vegetation, and disease dynamics endogenously. The parameters used here represent a Bayesian posterior, from MCMC with literature priors and a lot of data. The parameter sample from the posterior is a joint distribution that captures both individual parameter variation and covariation (though with only a few exceptions things seem to be relatively independent).

Here’s the effect of parameter uncertainty on the disease trajectory:

Each of the 10,000 runs making up this ensemble is deterministic. It’s surprisingly tight, because it is well-determined by the data.

However, parameter uncertainty is not the only issue. Even if you know the actual state of the disease perfectly, there’s still uncertainty in the reported outcome due to sampling variation. You might stray from the “true” prevalence of the disease because of chance in the selection of which deer are actually tested. Making sampling stochastic broadens the bounds:

That’s still not the whole picture, because deer aren’t really deterministic. They come in integer quanta and they have random interactions. Thus a standard SD formulation like:

births = birth rate * doe population

becomes

births = Poisson( birth rate * doe population )

For stock outflows, like the transition from healthy to infected, the Binomial distribution may be the appropriate choice. This randomness in flows means there’s additional variance around the deterministic course, and the model can explore a wider set of trajectories.

There’s one other interesting feature, particularly evident in this last graph: uncertainty around the mean (i.e. the geometric standard deviation) varies quite a bit. Initially, uncertainty increases with time – as Yogi Berra said, “It’s tough to make predictions, especially about the future.” In the early stages of the disese (2003-2008 say), numbers are small and random events affect the timing of takeoff of the disease, amplified by future positive feedback. A deterministic disease model with reproduction ratio R0>1 can only grow, but in a stochastic model luck can cause the disease to go extinct or bumble around 0 prevalence for a while before emerging into growth. Towards the end of this simulation, the confidence bounds narrow. There are two reasons for this: negative feedback is starting to dominate as the disease approaches saturation prevalence, and at the same time the normalized standard deviation of the sampling errors and randomness in deer dynamics is decreasing as the numbers become larger (essentially with 1/sqrt(n)).

This is not uncommon in real systems. For example, you may be unsure where a chaotic pendulum will be in it’s swing a minute from now. But you can be pretty sure that after an hour or a day it will be hanging idle at dead center. However, this might not remain true when you broaden the boundary of the system to include additional feedbacks or disturbances. In this CWD model, for example, there’s some additional feedback from human behavior (not in the statistical model, but in the full version) that conditions the eventual saturation point, perhaps preventing convergence of uncertainty.

Postdoc @ UofM in SD for Wildlife Management


This is an interesting opportunity. The topic is important, it’s a hard problem, and it’s interesting both on the techy side and the people/process side. You can get a little flavor of recent CWD work here. The team is smart & nice, and supports competent and ethical resource managers on the ground. Best of all, it’s in Montana, though you do have to be a Griz instead of a Cat.

That QR code (and this link) points to the full job listing.