BBC UK writes, Coronavirus: Three reasons why the UK might not look like Italy. They point to three observations about the epidemic so far:
- Different early transmission – the UK lags the epidemic in Italy
- Italy’s epidemic is more concentrated
- More of Italy’s confirmed cases are fatal
I think these speculations are misguided, and give a potentially-disastrous impression that the UK might somehow dodge a bullet without really trying. That’s only slightly mitigated by the warning at the end,
Don’t relax quite yet
Even though our epidemic may not follow Italy’s exactly, that doesn’t mean the UK will escape serious changes to its way of life.
Epidemiologist Adam Kucharski warns against simple comparisons of case numbers and that “without efforts to control the virus we could still see a situation evolve like that in Italy”, even if not necessarily in the next four weeks.
… which should be in red 72-point text right at the top.
Will the epidemic play out differently in the UK? Surely. But it really look qualitatively different? I doubt it, unless the reaction is different.
The fundamental problem is that the structure of a system determines its behavior. A slinky will bounce if you jiggle it, but more fundamentally it bounces because it’s a spring. You can jiggle a brick all you want, but you won’t get much bouncing.
The system of a virus spreading through a population is the same. The structure of the system says that, as long as the virus can infect people faster than they recover, it grows exponentially. It’s inevitable; it’s what a virus does. The only way to change that is to change the structure of the system by slowing the reproduction. That happens when there’s no one left to infect, or when we artificially reduce the infection rate though social distancing, sterilization and quarantine.
A change to the initial timing or distribution of the epidemic doesn’t change the structure at all. The slinky is still a slinky, and the epidemic will still unfold exponentially. Our job, therefore, is to make ourselves into bricks.
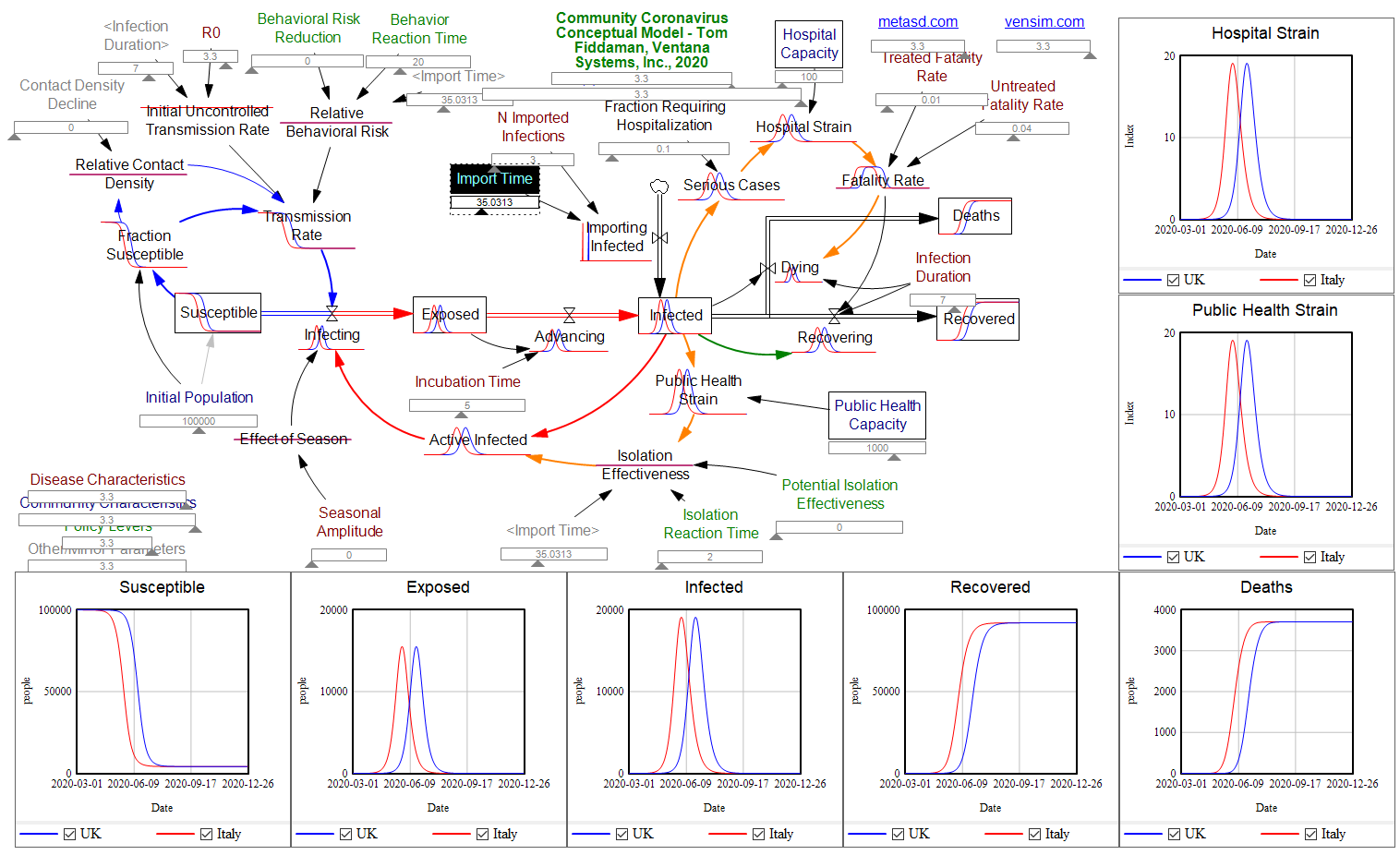
The third point, that fatality rates are lower, may also be a consequence of the UK starting from a different state today. In Italy, infections have grown high enough to overwhelm the health care system, which increases the fatality rate. The UK may not be there yet. However, a few doublings of the number of infected will quickly close the gap. This may also be an artifact of incomplete testing and lags in reporting.
Here’s a more detailed explanation:

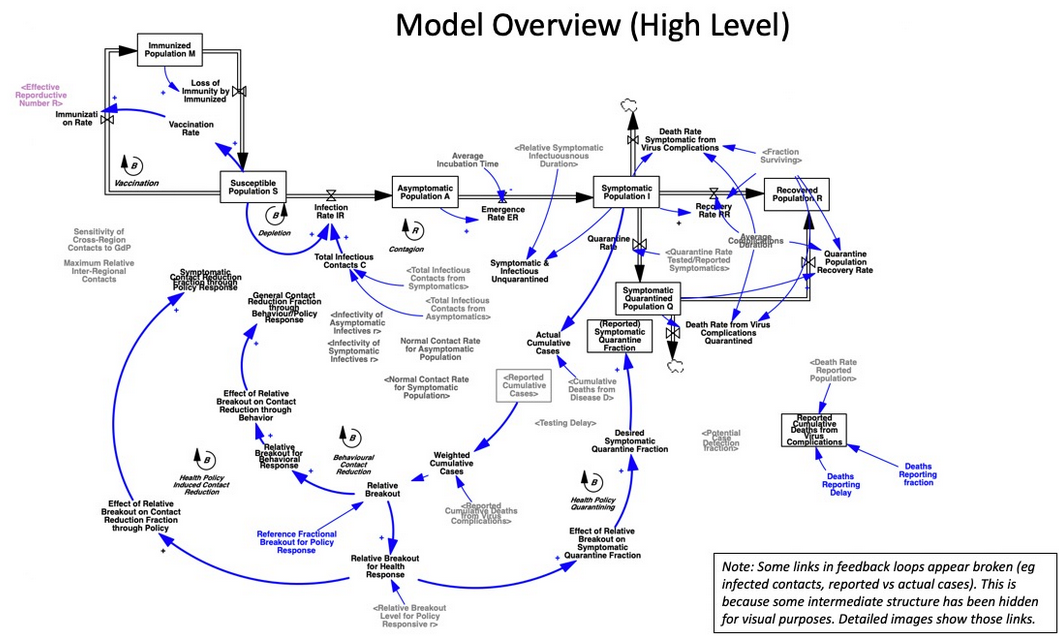

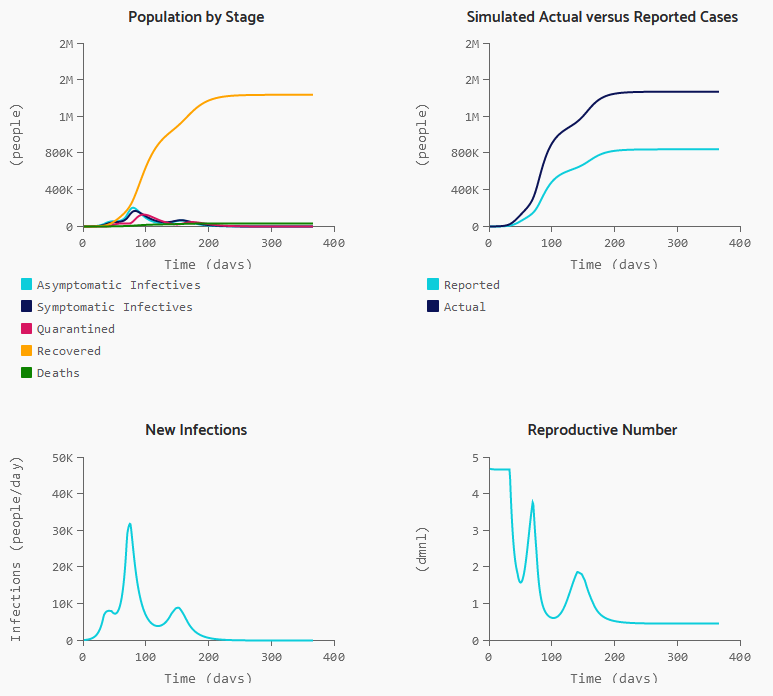
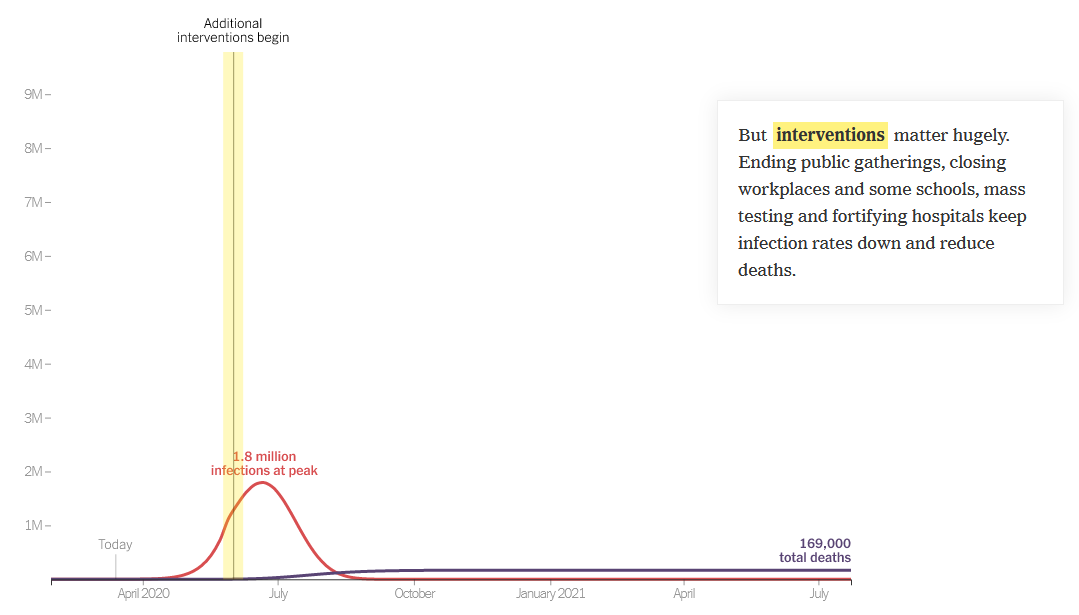


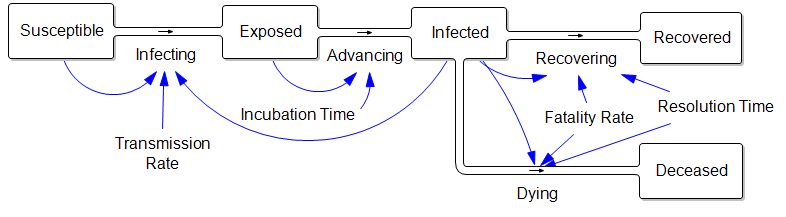
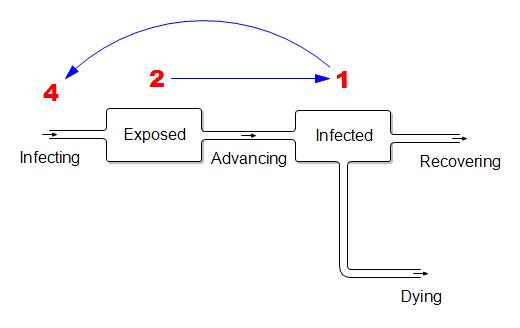
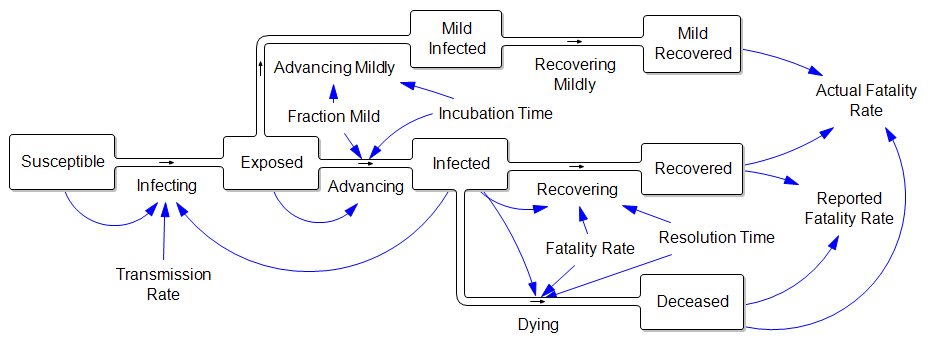
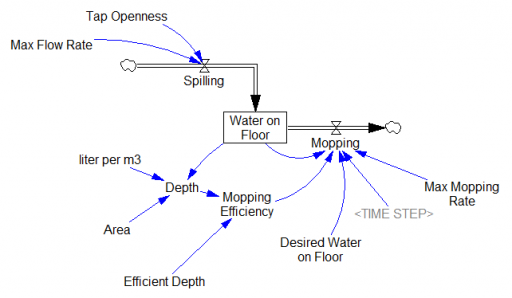
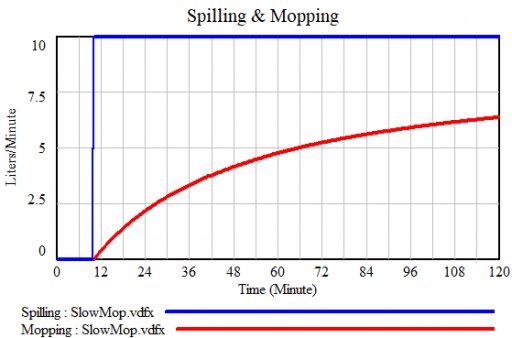
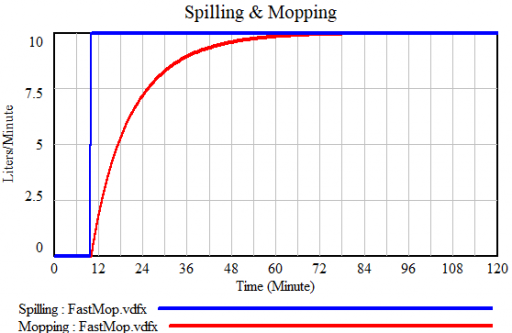
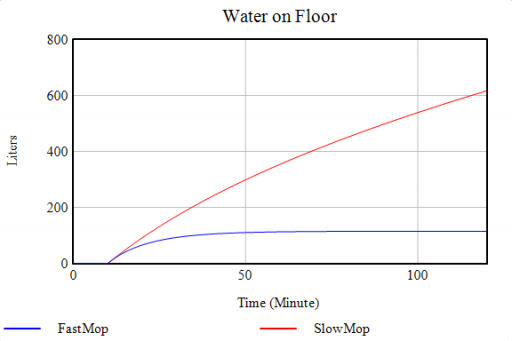
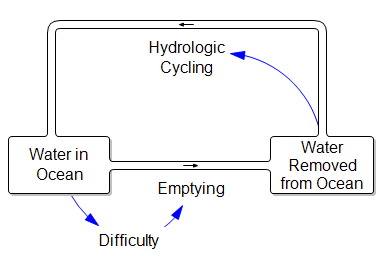
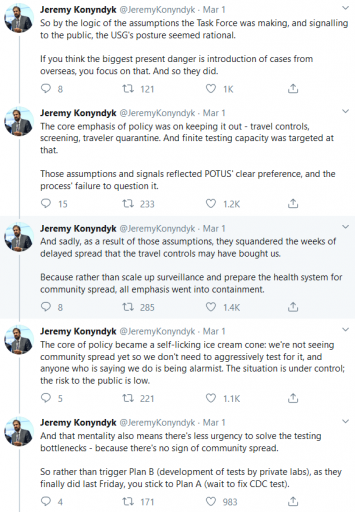
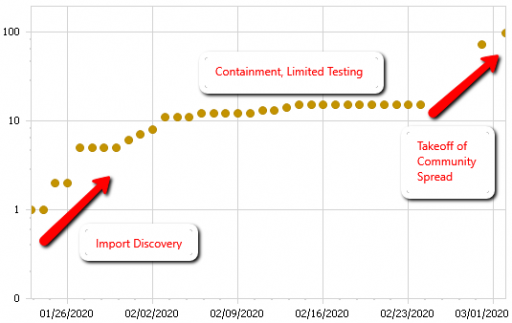
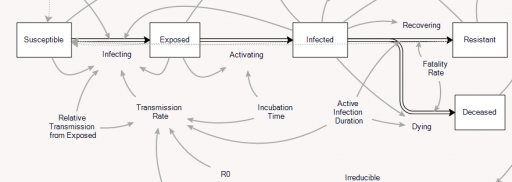 The problem is that containment alone doesn’t work, because the structure of the system defeats it. You can’t intercept every infected person, because some are exposed but not yet symptomatic, or have mild cases. As soon as a few of these people slip into the wild, the positive loops that drive infection operate as they always have. Once the virus is in the wild, it’s essential to change behavior enough to lower its reproduction below replacement.
The problem is that containment alone doesn’t work, because the structure of the system defeats it. You can’t intercept every infected person, because some are exposed but not yet symptomatic, or have mild cases. As soon as a few of these people slip into the wild, the positive loops that drive infection operate as they always have. Once the virus is in the wild, it’s essential to change behavior enough to lower its reproduction below replacement.