Vensim Archives - Page 2 of 3

Payments for Environmental Services

Model Name: payments, penalties, and environmental ethic

Citation: Dudley, R. 2007. Payments, penalties, payouts, and environmental ethics: a system dynamics examination Sustainability: Science, Practice, & Policy 3(2):24-35. http://ejournal.nbii.org/archives/vol3iss2/0706-013.dudley.html.

Source: Richard G. Dudley

Copyright: Richard G. Dudley (2007)

License: Gnu GPL

Peer reviewed: Yes (probably when submitted for publication?)

Units balance: Yes

Format: Vensim

Target audience: People interested in the concept of payments for environmental services as a means of improving land use and conservation of natural resources.

Questions answered: How might land users’ environmental ethic be influenced by, and influence, payments for environmental services.

Software: Vensim

Payments for Environmental Services (Vensim .vmf)

The Obscure Art of Datamodeling in Vensim

There are lots of good reasons for building models without data. However, if you want to measure something (i.e. estimate model parameters), produce results that are closely calibrated to history, or drive your model with historical inputs, you need data. Most statistical modeling you’ll see involves static or dynamically simple models and well-behaved datasets: nice flat files with uniform time steps, units matching (or, alarmingly, ignored), and no missing points. Things are generally much messier with a system dynamics model, which typically has broad scope and (one would hope) lots of dynamics. The diversity of data needed to accompany a model presents several challenges:

disagreement among sources
missing data points
non-uniform time intervals
variable quality of measurements
diverse source formats (spreadsheets, text files, databases)

The mathematics for handling the technical estimation problems were developed by Fred Schweppe and others at MIT decades ago. David Peterson’s thesis lays out the details for SD-type models, and most of the functionality described is built into Vensim. It’s also possible, of course, to go a simpler route; even hand calibration is often effective and reasonably quick when coupled with Synthesim.

Either way, you have to get your data corralled first. For a simple model, I’ll build the data right into the dynamic model. But for complicated models, I usually don’t want the main model bogged down with units conversions and links to a zillion files. In that case, I first build a separate datamodel, which does all the integration and passes cleaned-up series to the main model as a fast binary file (an ordinary Vensim .vdf). In creating the data infrastructure, I try to maximize three things:

Replicability. Minimize the number of manual steps in the process by making the data model do everything. Connect the datamodel directly to primary sources, in formats as close as possible to the original. Automate multiple steps with command scripts. Never use hand calculations scribbled on a piece of paper, unless you’re scrupulous about lab notebooks, or note the details in equations’ documentation field.
Transparency. Often this means “don’t do complex calculations in spreadsheets.” Spreadsheets are very good at some things, like serving as a data container that gives good visibility. However, spreadsheet calculations are error-prone and hard to audit. So, I try to do everything, from units conversions to interpolation, in Vensim.
Quality.#1 and #2 already go a long way toward ensuring quality. However, it’s possible to go further. First, actually look at the data. Take time to build a panel of on-screen graphs so that problems are instantly visible. Use a statistics or visualization package to explore it. Lately, I’ve been going a step farther, by writing Reality Checks to automatically test for discontinuities and other undesirable properties of spliced time series. This works well when the data is simply to voluminous to check manually.

This can be quite a bit of work up front, but the payoff is large: less model rework later, easy updates, and higher quality. It’s also easier generate graphics or statistics that help others to gain confidence in the model, though it’s sometimes important to help them recognize that goodness of fit is a weak test of quality.

It’s good to build the data infrastructure before you start modeling, because that way your drivers and quality control checks are in place as you build structure, so you avoid the pitfalls of an end-of-pipe inspection process. A frequent finding in our corporate work has been that cherished data is in fact rubbish, or means something quite different that what users have historically assumed. Ventana colleague Bill Arthur argues that modern IT practices are making the situation worse, not better, because firms aren’t retaining data as long (perhaps a misplaced side effect of a mania for freshness).

Continue reading “The Obscure Art of Datamodeling in Vensim”

Data variables or lookups?

System dynamics models handle data in various ways. Traditionally, time series inputs were embedded in so-called lookups or table functions (DYNAMO users will remember TABHL for example). Lookups are really best suited for graphically describing a functional relationship. They’re really cool in Vensim’s Synthesim mode, where you can change the shape of a relationship and watch the behavioral consequence in real time.

Time series data can be thought of as f(time), so lookups are often used as data containers. This works decently when you have a limited amount of data, but isn’t really suitable for industrial strength modeling. Those familiar with advanced versions of Vensim may be aware of data variables – a special class of equation designed for working with time series data rather than endogenous structure.

There are many advantages to working with data variables:

You can tell where there are data points, visually on graphs or in equations by testing for a special :NA: value indicating missing data.
You can easily determine the endpoints of a series and vary the interpolation method.
Data variables execute outside the main sequence of the model, so they don’t bog down optimization or Synthesim.
It’s easier to use diverse sources for data (Excel, text files, ODBC, and other model runs) with data variables.
You can see the data directly, without creating extra variables to manipulate it.
In calibration optimization, data variables contribute to the payoff only when it makes sense (i.e., when there’s real data).

I think there are just two reasons to use lookups as containers for data:

You want compatibility with Vensim PLE (e.g., for students)
You want to expose the data stream to quick manipulation in a user interface

Otherwise, go for data variables. Occasionally, there are technical limitations that make it impossible to accomplish something with a data equation, but in those cases the solution is generally a separate data model rather than use of lookups. More on that soon.

Tableau + Vensim = ?

I’ve been testing a data mining and visualization tool called Tableau. It seems to be a hot topic in that world, and I can see why. It’s a very elegant way to access large database servers, slicing and dicing many different ways via a clean interface. It works equally well on small datasets in Excel. It’s very user-friendly, though it helps a lot to understand the relational or multidimensional data model you’re using. Plus it just looks good. I tried it out on some graphics I wanted to generate for a collaborative workshop on the Western Climate Initiative. Two examples:

A year or two back, I created a tool, based on VisAD, that uses the Vensim .dll to do multidimensional visualization of model output. It’s much cruder, but cooler in one way: it does interactive 3D. Anyway, I hoped that Tableau, used with Vensim, would be a good replacement for my unfinished tool.

After some experimentation, I think there’s a lot of potential, but it’s not going to be the match made in heaven that I hoped for. Cycle time is one obstacle: data can be exported from Vensim in .tab, .xls, or a relational table format (known as “data list” in the export dialog). If you go the text route (.tab), you have to pass through Excel to convert it to .csv, which Tableau reads. If you go the .xls route, you don’t need to pass through Excel, but may need to close/open the Tableau workspace to avoid file lock collisions. The relational format works, but yields a fundamentally different description of the data, which may be harder to work with.

I think where the pairing might really shine is with model output exported to a database server via Vensim’s ODBC features. I’m lukewarm on doing that with relational databases, because they just don’t get time series. A multidimensional database would be much better, but unfortunately I don’t have time to try at the moment.

Whether it works with models or not, Tableau is a nice tool, and I’d recommend a test drive.

http://www.ssec.wisc.edu/~billh/visad.html

Good modeling practices

Some thoughts I’ve been collecting, primarily oriented toward system dynamics modeling in Vensim, but relevant to any modeling endeavor:

Know why you’re building the model.
- If you’re targeting a presentation or paper, write the skeleton first, so you know how the model will fill in the answers as you go.
Organize your data first.
- No data? No problem. But surely you have some reference mode in mind, and some constraints on behavior, at least in extreme conditions.
- In Vensim, dump it all into a spreadsheet, database, or text file and import it into a data model, using the Model>Import data… feature, GET XLS DATA functions, or ODBC.
- Don’t put data in lookups (table functions) unless you must for some technical reason; they’re a hassle to edit and update, and lousy at distinguishing real data points from interpolation.
Keep a lab notebook. An open word processor while you work is useful. Write down hypotheses before you run, so that you won’t rationalize surprises. Continue reading “Good modeling practices”

Setting Up Vensim

I’m trying to adapt to the new tabbed interface in Office 2007. So far, all those pretty buttons seem like a hindrance. Vensim, on the other hand, is a bit too austere. I’ve just installed version 5.9 (check it out, and while you’re at it see the new Ventana site); my setup follows. Note that this only applies to advanced versions of Vensim.

First, I allow the equation editor to “accept enter” – I like to be able to add line breaks to equations (and hate accidentally dismissing the editor with an <enter>). You can do this anyway with <ctl><enter>, but I prefer it this way.

Continue reading “Setting Up Vensim”

Sea Level Rise – VI – The Bottom Line (Almost)

The pretty pictures look rather compelling, but we’re not quite done. A little QC is needed on the results. It turns out that there’s trouble in paradise:

the residuals (modeled vs. measured sea level) are noticeably autocorrelated. That means that the model’s assumed error structure (a white disturbance integrated into sea level, plus white measurement error) doesn’t capture what’s really going on. Either disturbances to sea level are correlated, or sea level measurements are subject to correlated errors, or both.
attempts to estimate the driving noise on sea level (as opposed to specifying it a priori) yield near-zero values.

#1 is not really a surprise; G discusses the sea level error structure at length and explicitly address it through a correlation matrix. (It’s not clear to me how they handle the flip side of the problem, state estimation with correlated driving noise – I think they ignore that.)

#2 might be a consequence of #1, but I haven’t wrapped my head around the result yet. A little experimentation shows the following:

driving noise SD	equilibrium sensitivity (a, mm/C)	time constant (tau, years)	sensitivity (a/tau, mm/yr/C)
~ 0 (1e-12)	94,000	30,000	3.2
1	14,000	4400	3.2
10	1600	420	3.8

Intermediate values yield values consistent with the above. Shorter time constants are consistent with expectations given higher driving noise (in effect, the model is getting estimated over shorter intervals), but the real point is that they’re all long, and all yield about the same sensitivity.

The obvious solution is to augment the model structure to include states representing persistent errors. At the moment, I’m out of time, so I’ll have to just speculate what that might show. Generally, autocorrelation of the errors is going to reduce the power of these results. That is, because there’s less information in the data than meets the eye (because the measurements aren’t fully independent), one will be less able to discriminate among parameters. In this model, I seriously doubt that the fundamental banana-ridge of the payoff surface is going to change. Its sides will be less steep, reflecting the diminished power, but that’s about it.

Assuming I’m right, where does that leave us? Basically, my hypotheses in Part IV were right. The likelihood surface for this model and data doesn’t permit much discrimination among time constants, other than ruling out short ones. R’s very-long-term paleo constraint for a (about 19,500 mm/C) and corresponding long tau is perfectly plausible. If anything, it’s more plausible than the short time constant for G’s Moberg experiment (in spite of a priori reasons to like G’s argument for dominance of short time constants in the transient response). The large variance among G’s experiment (estimated time constants of 208 to 1193 years) is not really surprising, given that large movements along the a/tau axis are possible without degrading fit to data. The one thing I really can’t replicate is G’s high sensitivities (6.3 and 8.2 mm/yr/C for the Moberg and Jones/Mann experiments, respectively). These seem to me to lie well off the a/tau ridgeline.

The conclusion that IPCC WG1 sea level rise is an underestimate is robust. I converted Part V’s random search experiment (using the optimizer) into sensitivity files, permitting Monte Carlo simulations forward to 2100, using the joint a-tau-T0 distribution as input. (See the setup in k-grid-sensi.vsc and k-grid-sensi-4x.vsc for details). I tried it two ways: the 21 points with a deviation of less than 2 in the payoff (corresponding with a 95% confidence interval), and the 94 points corresponding with a deviation of less than 8 (i.e., assuming that fixing the error structure would make things 4x less selective). Sea level in 2100 is distributed as follows:

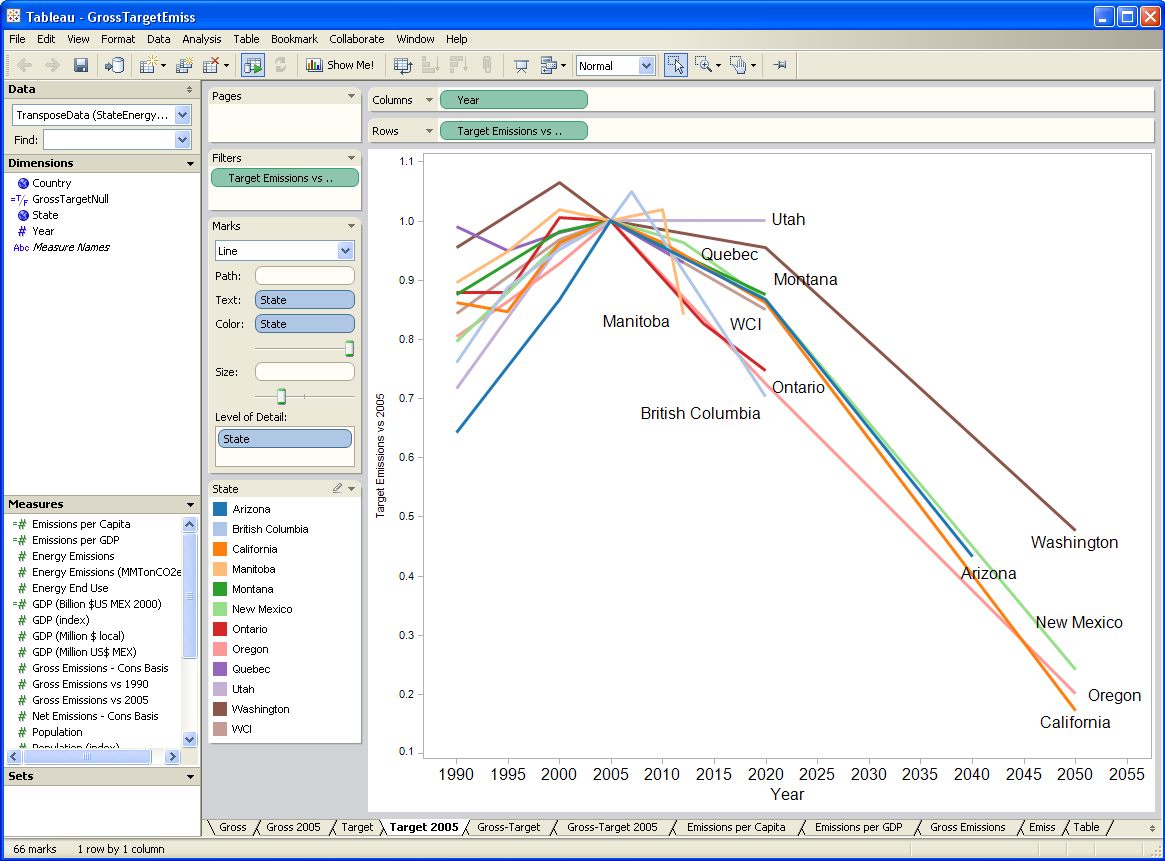
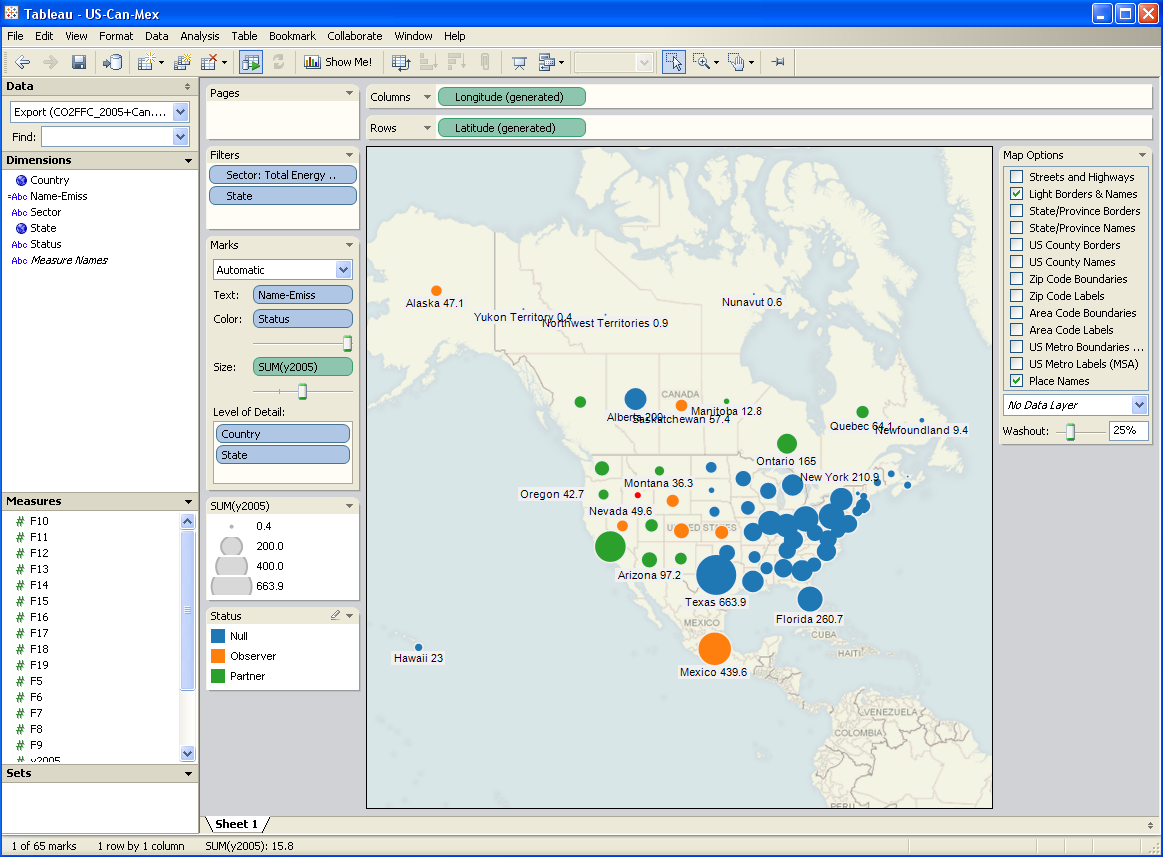
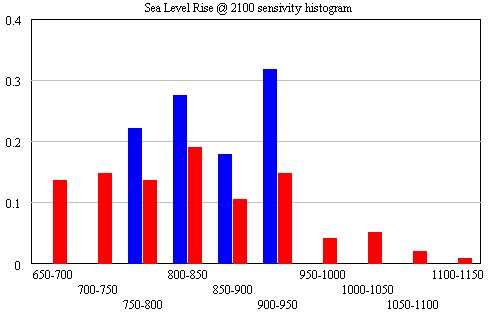
Sea level distribution in 2100

The sample would have to be bigger to reveal the true distribution (particularly for the “overconfident” version in blue), but the qualitative result is unlikely to change. All runs lie above the IPCC range (.26-.59), which excludes ice dynamics.

Continue reading “Sea Level Rise – VI – The Bottom Line (Almost)”

Sea Level Rise Models – V

To take a look at the payoff surface, we need to do more than the naive calibrations I’ve used so far. Those were adequate for choosing constant terms that aligned the model trajectory with the data, given a priori values of a and tau. But that approach could give flawed estimates and confidence bounds when used to estimate the full system.

Elaborating on my comment on estimation at the end of Part II, consider a simplified description of our model, in discrete time:

(1) sea_level(t) = f(sea_level(t-1), temperature, parameters) + driving_noise(t)

(2) measured_sea_level(t) = sea_level(t) + measurement_noise(t)

The driving noise reflects disturbances to the system state: in this case, random perturbations to sea level. Measurement noise is simply errors in assessing the true state of global sea level, which could arise from insufficient coverage or accuracy of instruments. In the simple case, where driving and measurement noise are both zero, measured and actual sea level are the same, so we have the following system:

(3) sea_level(t) = f(sea_level(t-1), temperature, parameters)

In this case, which is essentially what we’ve assumed so far, we can simply initialize the model, feed it temperature, and simulate forward in time. We can estimate the parameters by adjusting them to get a good fit. However, if there’s driving noise, as in (1), we could be making a big mistake, because the noise may move the real-world state of sea level far from the model trajectory, in which case we’d be using the wrong value of sea_level(t-1) on the right hand side of (1). In effect, the model would blunder ahead, ignoring most of the data.

In this situation, it’s better to use ordinary least squares (OLS), which we can implement by replacing modeled sea level in (1) with measured sea level:

(4) sea_level(t) = f(measured_sea_level(t-1), temperature, parameters)

In (4), we’re ignoring the model rather than the data. But that could be a bad move too, because if measurement noise is nonzero, the sea level data could be quite different from true sea level at any point in time.

The point of the Kalman Filter is to combine the model and data estimates of the true state of the system. To do that, we simulate the model forward in time. Each time we encounter a data point, we update the model state, taking account of the relative magnitude of the noise streams. If we think that measurement error is small and driving noise is large, the best bet is to move the model dramatically towards the data. On the other hand, if measurements are very noisy and driving noise is small, better to stick with the model trajectory, and move only a little bit towards the data. You can test this in the model by varying the driving noise and measurement error parameters in SyntheSim, and watching how the model trajectory varies.

The discussion above is adapted from David Peterson’s thesis, which has a more complete mathematical treatment. The approach is laid out in Fred Schweppe’s book, Uncertain Dynamic Systems, which is unfortunately out of print and pricey. As a substitute, I like Stengel’s Optimal Control and Estimation.

An example of Kalman Filtering in everyday devices is GPS. A GPS unit is designed to estimate the state of a system (its location in space) using noisy measurements (satellite signals). As I understand it, GPS units maintain a simple model of the dynamics of motion: my expected position in the future equals my current perceived position, plus perceived velocity times time elapsed. It then corrects its predictions as measurements allow. With a good view of four satellites, it can move quickly toward the data. In a heavily-treed valley, it’s better to update the predicted state slowly, rather than giving jumpy predictions. I don’t know whether handheld GPS units implement it, but it’s possible to estimate the noise variances from the data and model, and adapt the filter corrections on the fly as conditions change.

Continue reading “Sea Level Rise Models – V”

Sea Level Rise Models – IV

So far, I’ve established that the qualitative results of Rahmstorf (R) and Grinsted (G) can be reproduced. Exact replication has been elusive, but the list of loose ends (unresolved differences in data and so forth) is long enough that I’m not concerned that R and G made fatal errors. However, I haven’t made much progress against the other items on my original list of questions:

Is the Grinsted et al. argument from first principles, that the current sea level response is dominated by short time constants, reasonable?
Is Rahmstorf right to assert that Grinsted et al.’s determination of the sea level rise time constant is shaky?
What happens if you impose the long-horizon paleo constraint to equilibrium sea level rise in Rahmstorf’s RC figure on the Grinsted et al. model?

At this point I’ll reveal my working hypotheses (untested so far):

I agree with G that there are good reasons to think that the sea level response occurs over multiple time scales, and therefore that one could make a good argument for a substantial short-time-constant component in the current transient.
I agree with R that the estimation of long time constants from comparatively short data series is almost certainly shaky.
I suspect that R’s paleo constraint could be imposed without a significant degradation of the model fit (an apparent contradiction of G’s results).
In the end, I doubt the data will resolve the argument, and we’ll be left with the conclusion that R and G agree on: that the IPCC WGI sea level rise projection is an underestimate.

Continue reading “Sea Level Rise Models – IV”

Sea Level Rise Models – III

Starting from the Rahmstorf (R) parameterization (tested, but not exhaustively), let’s turn to Grinsted et al (G).

First, I’ve made a few changes to the model and supporting spreadsheet. The previous version ran with a small time step, because some of the tide data was monthly (or less). That wasted clock cycles and complicated computation of residual autocorrelations and the like. In this version, I binned the data into an annual window and shifted the time axes so that the model will use the appropriate end-of-year points (when Vensim has data with a finer time step than the model, it grabs the data point nearest each time step for comparison with model variables). I also retuned the mean adjustments to the sea level series. I didn’t change the temperature series, but made it easier to use pure-Moberg (as G did). Those changes necessitate a slight change to the R calibration, so I changed the default parameters to reflect that.

Now it should be possible to plug in G parameters, from Table 1 in the paper. First, using Moberg: a = 1290 (note that G uses meters while I’m using mm), tau = 208, b = 770 (corresponding with T0=-0.59), initial sea level = -2. The final time for the simulation is set to 1979, and only Moberg temperature data are used. The setup for this is in change files, GrinstedMoberg.cin and MobergOnly.cin.

Moberg, Grinsted parameters

Continue reading “Sea Level Rise Models – III”