Category: SystemDynamics

There’s a lot of art to modeling, and more generally to managing complex systems. But there’s also some craft to it: simple, mechanical steps that must be followed, almost without exception.  Woodworkers know that when you’re using a chisel or plane, you cut with the grain, not across it. Knowing that isn’t sufficient to make a nice-looking chair, but at least your funny-looking chair won’t have ugly tearout.

So what are the rules for classic System Dynamics? Here are a few:

1. Unbalanced or missing units. It’s possible to build a correct model without units, but most people (including me) are unlikely to manage it. Even if the model is right in some sense, without units it’s still unintelligible to others.
2. No FONFOO. Every physical stock needs First-Order Negative Feedback On the Outflows. This means the equations ensure that the outflow goes to 0 as the stock goes to 0 – not after a while, but now and forever. This ensures conservation of stuff: no inventory -> no sales. Nonphysical stocks often require this treatment as well, unless negative values are permitted by definition.
3. Embedded parameters. A colleague just found an equation in a spreadsheet model reading something like =A2*EXP(-C4/C1) + 4. The “4” was just an arbitrary fudge factor on the answer. This should never happen; anything more complex than the 1 in 1/x should always be exposed as a distinct, named variable with appropriate units.
   • Corollary: the embedded parameter often represents an implicit goal. For example, in inventory adjustment = (1000-inventory)/inventory adj time, the goal of 1000 units should be made explicit.
4. Discrete time. Generally, your model should be independent of the TIME STEP and simulation method. Decision rules should integrate information smoothly, not at arbitrary point lags.
5. Discrete logic. Sometimes I see equations that involve big cascades of logical statements: IF THEN ELSE( inventory < 100 :AND: price > 2, do x, IF THEN ELSE( inventory > 200 :AND: expected sales > inventory/desired coverage, do y, IF THEN ELSE( …  Constructions like this are hard to read and hard to debug, and they often fail important reality checks. They might be appropriate in tactical cases where reality has discernible, discrete rules. But they’re seldom helpful in strategic models involving the aggregate behavior of many agents or objects.
6. Overuse of delays. Every feedback loop must include a stock. This is a consequence of “time is what keeps everything from happening at once.” If there’s no integration in a loop, then feedback would run infinitely fast. Sometimes, confronted with an apparently simultaneous loop, modelers just insert a SMOOTHI or similar function that contains a stock. This may not be good enough; the stock in the loop can’t be arbitrary; it has to have real meaning.
   • It’s also possible to commit the opposite sin: underuse of delays. Perceptions lag reality, and people often underestimate the extent to which this is true. Decision rules in your model should reflect this, but I think it’s more a matter of art than craft.
7. Taking the cream out of the coffee. Suppose you have a stock of people, with a coflow of money used to keep track of the average wealth of people in the stock. It’s then tempting to handle a thought experiment like, “ok, what if all the rich people leave the country?” by siphoning off a greater-than-average share of the money alongside each departing person. This violates the assumption that a stock is the complete representation of system state. What if, for example, the rich people already left, so that the remainder are uniformly poor? If the distinction is important, you simply must disaggregate the people into classes.

Like all rules, these are made to be broken, but exceptions are rare, and require that you really know what you’re doing. They are important because they ensure compliance with Reality Checks that should remain inviolate for strong reasons. If your population model isn’t conserving people, you have a problem.

Incidentally, at least half of these are mentioned in Appendix O of Industrial Dynamics, “Beginners’ Difficulties.” However, these are not just tricks for beginners: everyone can benefit from keeping them in mind, just as professional pilots rely on checklists.

I’m eager to hear your thoughts in the comments. What rules did I miss?

See also:

How to critique a model (and build a model that withstands critique)

Towards Principles for Subscripting in Models

Dynamics of the last Twinkie

Misadventures with Little’s Law

* Update: edited slightly for parallelism of the headers.

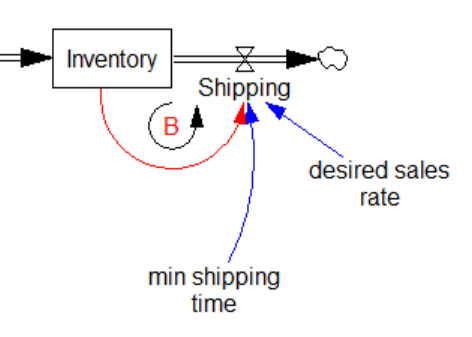
I’ve been approached several times recently with questions about stocks behaving badly. All involved a construction something like the following:

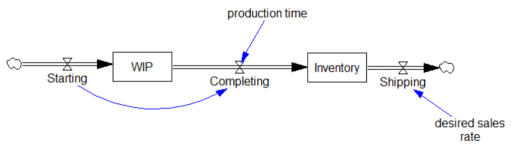
This is a simple inventory control system, in which I’ve short-circuited the production start feedback by making Starting exogenous and equal to the desired sales rate. Therefore, there are really only two interesting equations:

Shipping=desired sales rate
Units: widgets/Month

Completing=DELAY3( Starting, production time )
Units: widgets/Month

Notice that there’s a violation of standard practice here, in that there’s a flow-to-flow connection from Starting to Completing. This is due to the DELAY3 function, which is shorthand for an explicit 3rd-order delay:

The 3rd-order delay is often a realistic compromise between a 1st-order system, in which the first completions arrive too quickly after Starting, and a pipeline delay or conveyor, which has too little dispersion to represent an aggregation of many items. (See the Delay Sandbox and Erlang models for examples.)

So, how can we break this model?

I always like to start with some tests in Synthesim. A good one is to stress the system with a step in the desired sales rate, here from 100 to 120. You can immediately spot a problem:

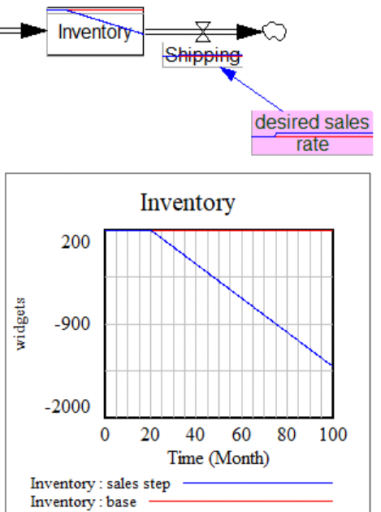
Inventory goes negative, because Shipping proceeds, even when inventory is exhausted. That can’t happen in reality, but it happens here because Shipping is not a function of Inventory. There’s a simple fix:

Shipping=MIN(desired sales rate, Inventory/min shipping time)
Units: widgets/Month

Above, min shipping time is a time constant representing the minimum time needed to deplete inventory. It’s common to set min shipping time = TIME STEP in situations where you want to prevent negative inventory, and the precise dynamics of inventory exhaustion are not central to the model. (If it matters, see Dynamics of the Last Twinkie.)

This is FONFOO. The “first order negative feedback” refers to the balancing loop created by the Inventory/min shipping time term in the fixed equation:

The tricky thing about this situation is that if Starting had been endogenous, the negative inventory problem would have been much harder to spot. Here’s the same model with a simple decision rule for Starting that maintains Inventory and WIP and desired levels:

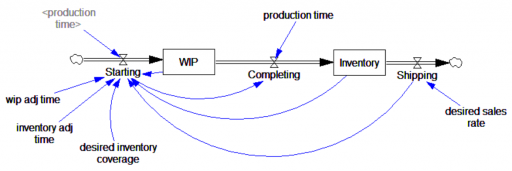
Now, a modest step in sales doesn’t cause negative inventory, as long as the production process can replenish it in time. It takes a huge step (from 100 to 400 widgets/month) to reveal the problem:

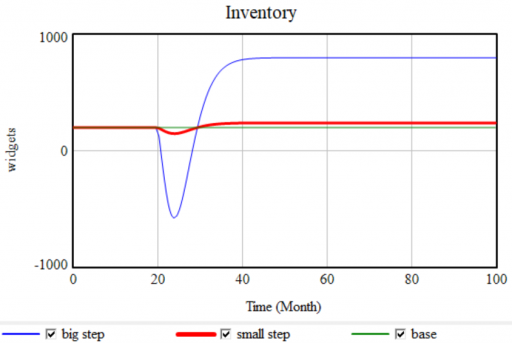
This means that experiments on a model as a whole may not reveal problems that lurk in the details of the model, unless they’re quite extreme. I recommend extreme tests, but prevention is more important. Simply make it a habit to implement FONFOO everywhere, and you won’t have problems. (Note that we could automate this in Vensim, but we don’t, because doing so can easily mask other formulation problems, fall short of the control that’s really needed, or impede situations in which nonphysical stocks are intentionally negative.)

Now let’s take a look at the 3rd-order production delay surrounding WIP. As presented above, it works fine – it’s mathematically equivalent to the explicit 3rd-order aging chain. However, there are consistency issues to be aware of. Consider the following augmentation of the structure, representing stock losses (the flow of Breaking) from WIP:

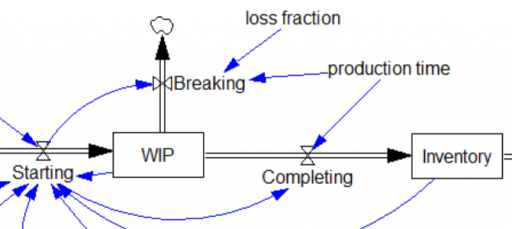
Completing=DELAY3( Starting, production time )
Units: widgets/Month
Breaking=DELAY3(Starting*loss fraction,production time)
Units: widgets/Month

Completing is still a delayed function of Starting. But Completing is not directly aware of WIP and therefore unaware of the consequences of Breaking. This is a violation of FONFOO because the DELAY3 function contains internal states that are independent of the WIP stock. Consider what happens if the loss fraction is nonzero. In equilibrium, the output of DELAY3 is equal to the inflow. So, the outflow from WIP would be Breaking+Completing, which equals Starting+Starting*loss fraction, which is of course greater than starting for any nonzero loss.

A step in the loss function from 0 to 0.2 causes WIP to go negative:

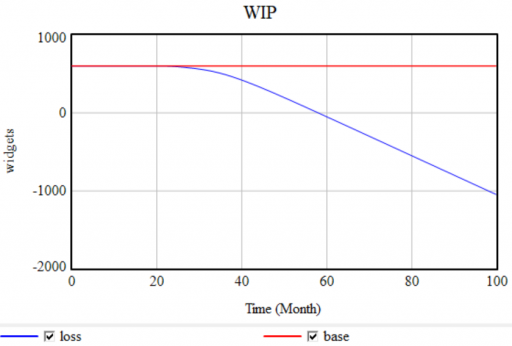
Again, the remedy is simple. In most cases, you can keep the DELAY function if you ensure that the inflows and outflows are conserved. For example, adding a term:

Completing=DELAY3( Starting*(1-loss fraction), production time )
 Units: widgets/Month
 Breaking=DELAY3(Starting*loss fraction,production time)
 Units: widgets/Month

In some situations, it may be desirable to switch to an explicit aging chain in order to handle an idiosyncratic distribution of losses across the WIP process, or other complexities. Often arrays are useful for such purposes.

You may encounter the DELAY1 function in similar circumstances. DELAY1 is just like DELAY3, except that it’s first order. So, the system:

inflow = 10 ~ widgets/month
stock = INTEG(inflow-outflow, inflow*tau) ~ widgets
outflow = stock/tau ~ widgets/month
tau = 6 ~ months

is identical to the system:

inflow = 10 ~ widgets/month
stock = INTEG(inflow-outflow, inflow*tau) ~ widgets
outflow = DELAY1(inflow,tau) ~ widgets/month
tau = 6 ~ months

In this case, there’s really no reason to use the DELAY1 – it just obfuscates the first-order stock dynamics. However, there’s still a potential pitfall, which also applies to DELAY3. The initialization is important. The DELAY functions generally initialize their internal stocks in equilibrium, as if the inflow had been at its initial level historically. Therefore the stock above needs to be initialized the same way, to inflow*tau. If you want to use some other value, like zero, you need to use DELAY3i (or its equivalent) to set the stock and delay function to a consistent set of assumptions.

In reviewing other models, you may also find hybrid approaches, like:

inflow = 10 ~ widgets/month
stock = INTEG(inflow-outflow, inflow*tau) ~ widgets
outflow = DELAY1(stock/tau,tau) ~ widgets/month
tau = 6 ~ months

This is another FONFOO violation. The outflow is indeed a function of the stock, which ensures that the outflow eventually goes to zero when the stock is exhausted. But this does not create a 1st-order negative feedback loop; the DELAY1 contains an additional stock. So, this is SONFOO (second order negative feedback on the outflow), which might be useful for creating an oscillator, but won’t solve your supply chain problems.

If you make FONFOO a habit, you’ll have one less thing to worry about when you start exploring the interesting, complex behaviors of your models.

On the SDwisdom blog, Jack Homer wonders whether we should be a little less endogenous:

The party line is that a model’s boundary should be broad enough so that the system’s main observed behaviors—such as S-shaped growth, oscillation, or overshoot and decline—are fully explained by the model’s endogenous structure.  One should avoid the use of exogenous time series drivers, because they undermine the ability of the model to explain and to anticipate change.

I mostly agree with this view but want to offer a friendly amendment here.  In my experience with real-world clients, I have often encountered situations in which it makes sense to employ exogenous time series for the sake of completeness and realism.

…

My experience suggests that we should be less doctrinaire about the endogenous perspective and understand that “endogenous” is a relative thing.  No model can be all-encompassing and explain all observed behavior patterns.  That’s why we define a model relative to some subset of behaviors also known as the dynamic problem.  As long as the model adequately addresses the dynamic problem, it shouldn’t really matter if the model has some exogenous time series included to improve the model’s realism.

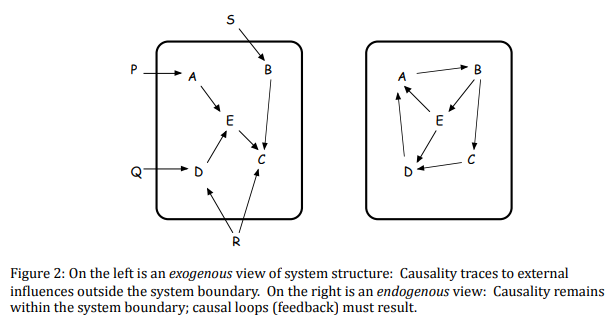
The counterpoint to this might be George Richardson’s excellent article on the value of an endogenous perspective:

But the foundation of systems thinking and system dynamics lies deeper than these and is often implicit or even ignored: it is the “endogenous point of view.” The paper will begin with historical background, clarify the endogenous point of view, illustrate with examples, and argue that the endogenous point of view is the sine%qua%non of systems approaches.

The dead buffalo model on the left in Richardson’s figure is perhaps too extreme. I think what Homer is really arguing for is a middle road that might look like this:

In other words, it’s a hybrid model, with an endogenous core, and a few exogenous drivers from beyond the model boundary. For a firm, this might mean that we model the interactions of marketing, production, human resources, etc. endogenously. But we leave the world crude price and GDP of France exogenous, because we have no plausible means to influence them.

Richardson points out, in the context of Urban Dynamics:

How might thinking exogenously have affected conclusions emerging from these urban models? Consider just one: suppose, as a number of critics of various system dynamics studies have suggested, we chose to use time series data for urban population projections. Suppose the data-based projections were very carefully developed by sophisticated statistical tools and econometric methods, and suppose those projections were fed into URBAN1 in place of the endogenous stock of population. To make the implications easiest to see, let’s suppose the base run of the model looks just as it did in Figure 5b. What would Figure 5c look like? Sadly, population would not show a bump as it did in 5c because the sophisticated exogenous time series data would not be influenced in the slightest by the changing conditions in the model. We would not see the compensating urban migration effects we see in Figure 5c, and we would miss the crucial conclusion that population and business construction dynamics would naturally compensate for the jobs program. We’d probably think it was a long term policy success, and we would be dramatically wrong.

Similarly, a key part of my dissertation critique of the DICE model was the idea that its exogenous representation of technology excluded a set competitive dynamics between fossil fuels and renewables that are crucial to understanding climate policy. In both cases, leaving even a few loops exogenous might dramatically alter policy recommendations.

In another article, Homer rejoins:

In 1977, my teacher, SD pioneer Ed Roberts, wrote an important paper called “Strategies for Effective Implementation of Complex Corporate Models”, based on his years of consulting experience.  When it comes to policy recommendations, he said, “the organizations’ ability to absorb the associated change must be assessed…The model-builder and the organization both profit from implementation of moderate change proposals leading to some successful results; both lose from grandiose plans which fail to be moved ahead.”

…

Without too much extra effort beyond what we already do in modeling, we could assess policy feasibility by studying the political situation and its dynamics, looking at trends in public opinion surveys and other indicator data, and talking to experts. We could then calculate the “feasibility-adjusted value” of a policy by multiplying its potential impact (as determined by our SD model) by its likelihood of enactment.

In other words, one might ask, what good is it to know the nature of the best endogenous policy if the key leverage points are beyond your control? Or, as economists put it, what good are first-best policies in a second-best world?

I think Richardson might respond along the lines of Pascal’s wager:

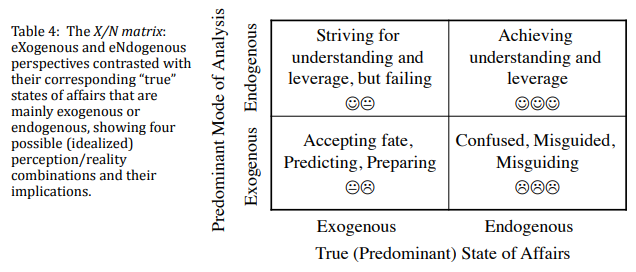
To the extent that we accept some exogeneity in our models, we accept our fate in the lower left box. That choice presumes that our best strategy is to do a good job of predicting and preparing – making the best of a bad situation, or living to fight another day. Is that really a good idea – can we know, or at least make a good guess, whether the true state of affairs is exogenous or endogenous? Richardson argues that if we don’t know which box we’re in, it’s best to choose the endogenous approach:

If one were to recast Table 4 as a decision tree, the decision to take an endogenous point of view in all circumstances would have the highest net payoff, at least in terms of happy faces and the real feelings they represent. An endogenous point of view is potentially empowering, and that feels good to us.

If the right (endogenous) side of the diagram is better in some sense, we should ask a more important question: can we change the state of affairs, so that we can move from the left quadrants to the right? This is related to the idea that we might need to change paradigms to change the system.

This perspective is especially critical for problems like climate change, where the space of politically feasible policies currently does not include anything that actually solves the problem. Treating the infeasible loops as exogenous drivers won’t help. We need to ask, what loops that are now beyond our control can be activated in order to reach a more attractive solution?

Maybe there really is no good solution to climate and other Limits problems. Then perhaps it would be optimal in some sense to take catastrophe as exogenous and use models to plan a personal path through the eye of the storm. Personally, I’m not ready to accept that. My modeling objective remains to die with my boots on tackling the biggest problems.

See also:

Closing loops – practicalities

Why the World Loves Open Loop Models

What kind of model should I use?